专题04 立体几何（测试卷）（新课标版）备战2017年高考数学（理）二轮复习精品资料

专题04 立体几何（测试卷）（新课标版）备战2017年高考数学（理）二轮复习精品资料

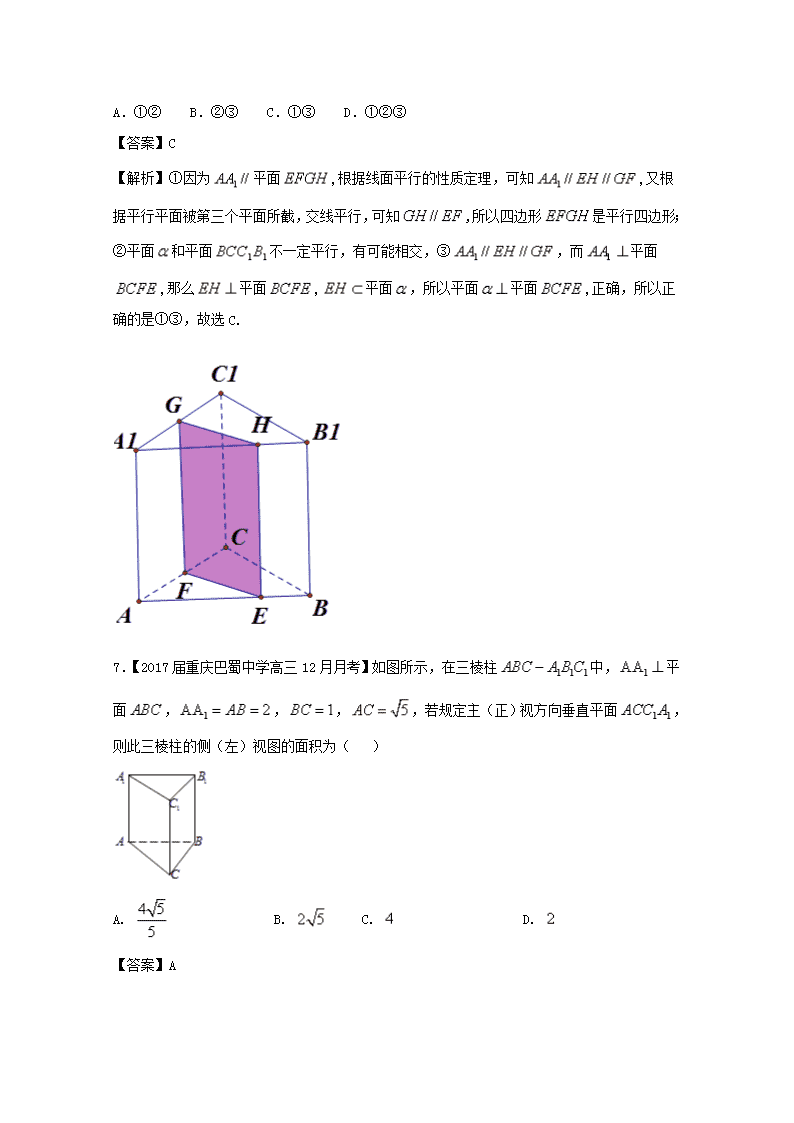
www.ks5u.com ‎【高效整合篇】‎ ‎ 专题四 立体几何 ‎（一）选择题（12*5=60分）‎ ‎1．【2017届广东省高三上学期阶段性测评一】三棱柱的侧棱垂直于底面，且，，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎2．【重庆市第八中学2017届高三上学期第二次适应性考试】已知，，是三个不同的平面， ，是两条不同的直线，下列命题是真命题的是（ ）‎ A．若，，则 B．若，，则 C．若，，，则 D．若，，，则 ‎【答案】D ‎【解析】对于A，B选项，可能相交；对于C选项，可能异面，故选D.‎ ‎3．【广西高级中学2017届高三11月阶段性检测】三棱锥的每个顶点都在表面积为的球的球面上，且平面，△为等边三角形，，则三棱锥的体积为（ ）‎ A．3 B． C． D．‎ ‎【答案】C ‎【解析】因为球的表面积为，所以球半径为，设△的边长为，则，由正三角形的性质可知△外接圆直径，根据球的性质可得 ‎，解得，三棱锥的体积为：，故选C. ‎ ‎4．【2017届河北衡水中学高三12月月考】《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著．其第五卷《商功》中有如下问题：“今有圆堡，周四丈八尺，高一丈一尺，问积几何？”这里所说的圆堡就是圆柱体，其底面周长是4丈8尺，高1丈1尺，问它的体积是多少?若取3，估算该圆堡的体积为（1丈=10尺）（ ）‎ A．1998立方尺 B．2012立方尺 C．2112立方尺 D．2324立方尺 ‎【答案】A ‎【解析】由底面半径为，则，又，所以，所以该圆堡的体积为立方尺，故选A．‎ ‎5．【2017届河南中原名校豫南九校高三上学期质检四】在直三棱柱中，，点是侧面内的一点，若与平面所成的角为，与平面所成的角也为，则与平面所成的角正弦值为（ ）‎ A． B． C. D．‎ ‎【答案】B ‎6．【2017届四川成都市高三一诊考试】在直三棱柱中，平面与棱分别交于点，且直线平面.有下列三个命题：①四边形是平行四边形；②平面平面；③平面平面.其中正确的命题有（ ）．‎ A．①② B．②③ C．①③ D．①②③‎ ‎【答案】C ‎【解析】①因为平面,根据线面平行的性质定理，可知,又根据平行平面被第三个平面所截，交线平行，可知,所以四边形是平行四边形；②平面和平面不一定平行，有可能相交，③，而平面,那么平面,平面，所以平面平面,正确，所以正确的是①③，故选C.‎ ‎7．【2017届重庆巴蜀中学高三12月月考】如图所示，在三棱柱中，平面，，，，若规定主（正）视方向垂直平面，则此三棱柱的侧（左）视图的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎8．【2017届河北唐山市高三数上学期期末】现有一半球形原料，若通过切削将该原料加工成一正方体工件，则所得工件体积与原料体积之比的最大值为 （ ）‎ A． B． C. D．‎ ‎【答案】A ‎9．【2017届湖南五市十校高三12月联考】圆锥的母线长为，过顶点的最大截面的面积为，则圆锥底面半径与母线长的比的取值范围是（ ）．‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由题意得轴截面的顶角不小于，因为，所以，选D.‎ ‎10．【2017届辽宁庄河市高级中学高三12月月考】已知长方体的外接球的体积为，其中，则三棱锥的体积的最大值为（ ）‎ A.1 B.3 C.2 D.4‎ ‎【答案】A ‎【解析】由题意设外接球的半径为,则由题设可得,由此可得 ‎.记长方体的三条棱长分别为,则,由此可得,因棱锥的体积,故应选A.‎ ‎11．【2017届河北磁县一中高三11月月考】在正四棱锥中，为正方形的中心，，且平面与直线交于，则（ ）‎ A. B. C. D.‎ ‎【答案】A ‎12．【2017届重庆市第八中学高三上学期二调】用半径为的圆铁皮剪一个内接矩形，再以内接矩形的两边分别作为圆柱的高于底面半径，则圆柱的体积最大时，该圆铁皮面积与其内接矩形的面积比为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】设圆柱的高为，则其内接矩形的一边长为，那么另一边长为 ‎，所以圆柱的体积为，，令，得；令，得，即在内单调递增，在内单调递减，所以当时，此圆柱体积最大，那么另一边长为，故圆铁皮的面积和其内接矩形的面积比为，故选C.‎ ‎（二）填空题（4*5=20分）‎ ‎13．【贵州省遵义市2017届高三上学期第一次联考（期中）】已知平面截一球面得圆，过圆的圆心的平面与平面所成二面角的大小为60°，平面截该球面得圆，若该球的表面积为，圆的面积为，则圆的半径为__________．‎ ‎【答案】‎ ‎14．【河南省郑州市第一中学2017届高三上学期期中】已知球的表面积为，用一个平面截球，使截面圆的半径为，则截面圆心与球心的距离是____________．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：由已知可得．‎ ‎15．【2017届河北沧州一中高三11月月考】已知三棱锥的顶点都在同一个球面上（球），且，，当三棱锥的三个侧面的面积之和最大时，该三棱锥的体积与球的体积的比值是 .‎ ‎【答案】‎ ‎【解析】由于三条棱长是定值,所以由题设可知当两两互相垂直时,三个侧面的面积之和最大.在此前提下可构造长方体,使得分别是该长方体的长，宽，高.由此可得其外接球的直径即长方体的对角线长为,即球的半径,球的体积,而三棱锥的体积,所以,故应填答案.‎ ‎16．【2017届河南中原名校高三上质检三】如图，在棱长均相等的正四棱锥最终，为底面正方形的重心，分别为侧棱的中点，有下列结论：‎ ①平面；‎ ②平面平面；‎ ③； ‎ ④直线与直线所成角的大小为.‎ 其中正确结论的序号是 .（写出所有正确结论的序号）‎ ‎【答案】①②③‎ ‎【解析】如图，连接，易得，所以平面，结论①正确.同理，所以平面平面，结论②正确.由于四棱锥的棱长均相等，所以，所以，又，所以，结论③正确.由于分别为侧棱的中点，所以，又四边形为正方形，所以，所以直线与直线所成的角即为直线与直线所成的角，为 ‎，知三角形为等边三角形，所以，故④错误，故答案为①②③ .‎ ‎（三）解答题（10+5*12=70分）‎ ‎17．【2017届湖南湘中名校教改联合体高三12月联考】如图所示的几何体为一简单组合体，在底面中，，，，平面，，，．‎ ‎（1）求证：平面平面；‎ ‎（2）求该组合体的体积．‎ ‎【解析】（1）证明：因为平面，，所以平面．又因为平面，所以，又因为，且，所以平面，又因为平面，所以平面平面． ‎ ‎18．【2017届江苏如东高级中学等四校高三12月联考】如图，在四面体中，，，点，分别为棱，上的点，点为棱的中点，且平面平面．求证：‎ ‎（1）；‎ ‎（2）平面平面．‎ ‎【解析】（1）因为平面平面，平面平面，平面平面，‎ 所以，又为的中点，故为的中点，同理可得，为的中点，所以． ‎ ‎（2）因为，由（1）知，为的中点，所以，又，即，由（1）知，，所以，‎ 又，，平面，所以平面，又平面，故平面平面．‎ ‎19．【2017届辽宁盘锦高级中学高三11月月考】．如图，四棱锥中，底面，，，，为的中点，．‎ ‎（1）求的长；‎ ‎（2）求二面角的正弦值．‎ ‎【解析】（1）如图，连接交于点，∵，平分角，∴，以为坐标原点，、所在直线分别为轴、轴，建立空间直角坐标系，‎ 则，而，可得，又∵，‎ ‎∴可得，，，，由于⊥底面，可设，‎ ‎∵为边的中点，∴，由此可得，∵，且，‎ ‎∴，解得（舍负），因此，，可得的长为．‎ ‎（2）由（1）知，，，设平面的法向量为，平面的法向量为，∵，且，∴，取，得，同理，由且，解出．∴向量，的夹角余弦值为，因此，二面角 的正弦值等于．‎ ‎20．【河南省郑州市第一中学2017届高三上学期期中】如图，四棱锥中，底面为平行四边形，底面，是棱的中点，且．‎ ‎（1）求证：平面；‎ ‎（2）如果是棱上一点，且直线与平面所成角的正弦值为，求的值．‎ ‎【解析】（1）连结，因为在中，，所以，‎ 所以．因为，所以．　又因为底面，所以，因为，所以平面． ‎ ‎（2）‎ 如图以为原点，所在直线分别为轴建立空间直角坐标系，则．因为是棱的中点，所以 ‎．所以，设为平面的法向量，所以，即，令，则，所以平面的法向量．因为是在棱上一点，所以设．设直线与平面所成角为，因为平面的法向量，所以．解得，即，所以．‎ ‎21．【河南省新乡市2017届高三上学期第一次调研】如图①所示，四边形为等腰梯形，，且于点为的中点．将沿着折起至的位置，得到如图②所示的四棱锥.‎ ‎（1）求证：平面；‎ ‎（2）若平面平面，求二面角的余弦值．‎ ‎【解析】（1）取的中点，连接．∵为的中点，∴，且，∵图①中四边形为等腰梯形，，且，∴，∴，∴四边形为平行四边形，∴，∵平面平面，∴平面． ‎ ‎22．【2017届河南新乡一中高三周考11.6】如下图，在多面体中，⊥平面,,且是边长为2的等边三角形，,与平面所成角的正弦值为.‎ ‎（1）若是线段的中点，证明：⊥面；‎ ‎（2）求二面角的平面角的余弦值．‎ ‎【解析】（1）取AB的中点，连结,则面，∴即是与平面所成角, ，取的中点为,以为原点，为轴，为轴，为轴建立如图空间直角坐标系，则 ‎,取的中点为,则面 ‎ ‎,所以，所以面.‎ ‎（2）解：由上面知：面，又），取平面的一个法向量 又,,由此得平面的一个法向量，则 ‎ ‎