【数学】2020届一轮复习人教B版43空间几何中的向量方法练习

【数学】2020届一轮复习人教B版43空间几何中的向量方法练习

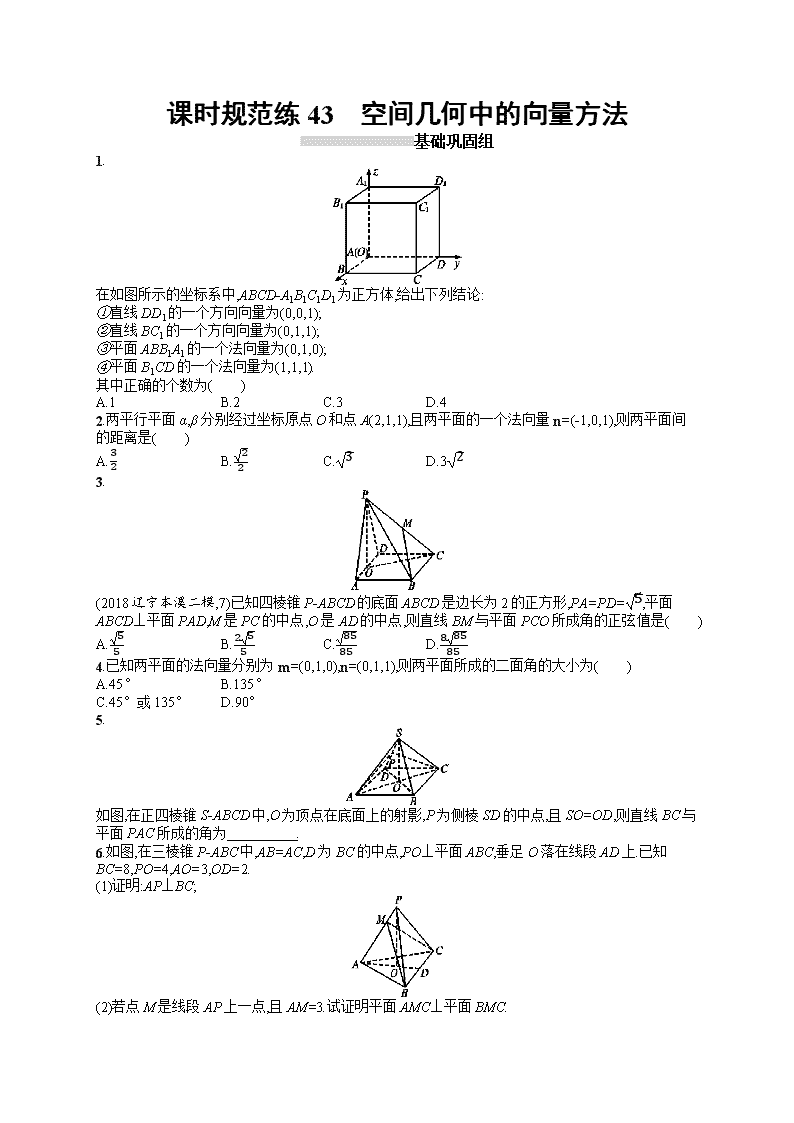
课时规范练43　空间几何中的向量方法 基础巩固组 ‎1.‎ 在如图所示的坐标系中,ABCD-A1B1C1D1为正方体,给出下列结论:‎ ‎①直线DD1的一个方向向量为(0,0,1);‎ ‎②直线BC1的一个方向向量为(0,1,1);‎ ‎③平面ABB1A1的一个法向量为(0,1,0);‎ ‎④平面B1CD的一个法向量为(1,1,1).‎ 其中正确的个数为(　　)‎ A.1 B.2 C.3 D.4‎ ‎2.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是(　　)‎ A.‎3‎‎2‎ B.‎2‎‎2‎ C.‎3‎ D.3‎‎2‎ ‎3.‎ ‎(2018辽宁本溪二模,7)已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PA=PD=‎5‎,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是(　　)‎ A.‎5‎‎5‎ B.‎2‎‎5‎‎5‎ C.‎85‎‎85‎ D.‎‎8‎‎85‎‎85‎ ‎4.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角的大小为(　　)‎ A.45° B.135°‎ C.45°或135° D.90°‎ ‎5.‎ 如图,在正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角为　　　　　. ‎ ‎6.如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.已知BC=8,PO=4,AO=3,OD=2.‎ ‎(1)证明:AP⊥BC;‎ ‎(2)若点M是线段AP上一点,且AM=3.试证明平面AMC⊥平面BMC.‎ ‎7.‎ 在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.‎ ‎(1)求证:B1C∥平面A1BD;‎ ‎(2)求点B1到平面A1BD的距离.‎ 综合提升组 ‎8.‎ ‎(2018安徽定远调研,10)如图,正方体ABCD-A1B1C1D1的棱长为1,中心为O,BF=‎1‎‎2‎BC,A1E=‎1‎‎4‎A1A,则四面体OEBF的体积为(　　)‎ A.‎1‎‎12‎ B.‎1‎‎24‎ C.‎1‎‎48‎ D.‎‎1‎‎96‎ ‎9.设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记D‎1‎PD‎1‎B=λ.当∠APC为锐角时,λ的取值范围是　　　　　. ‎ ‎10.‎ ‎(2019四川成都一模,19)在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,AD‎1‎‎2‎BC,AD=AE=1,∠ABC=60°,EF‎1‎‎2‎AC.‎ ‎(1)证明:AB⊥CF;‎ ‎(2)求二面角B-EF-D的余弦值.‎ ‎11.‎ ‎(2018河北衡水模拟二,18)如图所示,CC1⊥平面ABC,平面ABB1A1⊥平面ABC,四边形ABB1A1为正方形,∠ABC=60°,BC=CC1=‎1‎‎2‎AB=2,点E在棱BB1上.‎ ‎(1)若F为A1B1的中点,E为BB1的中点,证明:平面EC1F∥平面A1CB;‎ ‎(2)设BE=λBB‎1‎,是否存在λ,使得平面A1EC1⊥平面A1EC?若存在,求出λ的值;若不存在,请说明理由.‎ ‎12.‎ ‎(2018河北衡水中学适应性考试,18)如图,三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点.‎ ‎(1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;‎ ‎(2)若二面角B1-PQ-C1的平面角的余弦值为‎13‎‎13‎,求点P到平面BQB1的距离.‎ 创新应用组 ‎13.‎ ‎(2018江西南昌七模,18)如图,四棱锥P-ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.若PA=2‎3‎,且PA与底面ABCD所成角的正切值为‎2‎‎2‎.‎ ‎(1)证明:平面PAB⊥平面PBC;‎ ‎(2)E是线段CD上一点,记DEDC=λ(0<λ<1),是否存在实数λ,使二面角P-AE-C的余弦值为‎6‎‎6‎?若存在,求出λ的值;若不存在,请说明理由.‎ ‎14.‎ ‎(2018河南信阳二模,19)在三棱锥A-BCD中,AB=AD=BD=2,BC=DC=‎2‎,AC=2.‎ ‎(1)求证:BD⊥AC;‎ ‎(2)点P为AC上一动点,设θ为直线BP与平面ACD所形成的角,求sin θ的最大值.‎ 课时规范练43　空间几何中的向量方法 ‎1.C　∵DD1∥AA1,AA‎1‎=(0,0,1),故①正确;BC1∥AD1,AD‎1‎=(0,1,1),故②正确;直线AD⊥平面ABB1A1,AD=(0,1,0),故③正确;点C1的坐标为(1,1,1),AC‎1‎与平面B1CD不垂直,故④错.‎ ‎2.B　两平面的一个单位法向量n0=‎-‎2‎‎2‎,0,‎‎2‎‎2‎,故两平面间的距离d=|OA‎·‎n0|=‎‎2‎‎2‎‎.‎ ‎3.D　以O为原点,以OA‎、AB和OP为x轴,y轴,z轴正方向,建立空间直角坐标系,如图所示.由题可知O(0,0,0),P(0,0,2),B(1,2,0),C(-1,2,0),则OP=(0,0,2),OC=(-1,2,0),‎ ‎∵M是PC的中点,∴M-‎1‎‎2‎,1,1,BM=-‎3‎‎2‎,-1,1.‎ 设平面PCO的法向量n=(x,y,z),直线BM与平面PCO所成角为θ,‎ 则n·OP=2z=0,‎n·OC=-x+2y=0,‎可取n=(2,1,0),‎ sin θ=|cos|=‎|BM·n|‎‎|BM|·|n|‎‎=‎4‎‎17‎‎4‎‎×‎‎5‎=‎8‎‎85‎‎85‎.‎故选D.‎ ‎4.C　∵两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角与相等或互补,∵cos=m·n‎|m|·|n|‎‎=‎1‎‎1×‎‎2‎=‎‎2‎‎2‎,故=45°.故两平面所成的二面角为45°或135°,故选C.‎ ‎5.30°　如图所示,以O为原点建立空间直角坐标系.‎ 设OD=SO=OA=OB=OC=a,则A(a,0,0),B(0,a,0),C(-a,0,0),P‎0,-a‎2‎,‎a‎2‎‎.‎则CA=(2a,0,0),AP‎=‎-a,-a‎2‎,‎a‎2‎,‎CB=(a,a,0).‎ 设平面PAC的法向量为n,可求得n=(0,1,1),则cos=CB‎·n‎|CB||n|‎‎=a‎2‎a‎2‎‎·‎‎2‎=‎1‎‎2‎.∴‎=60°,‎ ‎∴直线BC与平面PAC所成角为90°-60°=30°.‎ ‎6.证明 ‎ ‎(1)如图所示,以O为坐标原点,以射线OP为z轴的正半轴建立空间直角坐标系.则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0),P(0,0,4).‎ 于是AP=(0,3,4),‎ BC‎=(-8,0,0),‎ ‎∴AP·‎BC‎=(0,3,4)·(-8,0,0)=0,‎ ‎∴AP⊥‎BC‎,即AP⊥BC.‎ ‎(2)由(1)知|AP|=5,又|AM|=3,且点M在线段AP上,‎ ‎∴AM=‎3‎‎5‎AP=‎‎0,‎9‎‎5‎,‎‎12‎‎5‎‎,‎ 又BA=(-4,-5,0),‎ ‎∴BM=BA+AM=‎‎-4,-‎16‎‎5‎,‎‎12‎‎5‎‎,则AP‎·‎BM=(0,3,4)‎·‎‎-4,-‎16‎‎5‎,‎‎12‎‎5‎=0,‎∴AP⊥‎BM,即AP⊥BM,‎ 又根据(1)的结论知AP⊥BC,‎ ‎∴AP⊥平面BMC,于是AM⊥平面BMC.‎ 又AM⊂平面AMC,故平面AMC⊥平面BCM.‎ ‎7.(1)证明 连接AB1交A1B于点E,连接DE.‎ 可知E为AB1的中点,D是AC的中点,∴DE∥B1C.‎ 又DE⊂平面A1BD,B1C⊄平面A1BD,∴B1C∥平面A1BD.‎ ‎(2)解 建立如图所示的空间直角坐标系,则B1(0,2‎2‎,3),B(0,2‎2‎,0),A1(-1,0,3),DB‎1‎=(0,2‎2‎,3),DB=(0,2‎2‎,0),DA‎1‎=(-1,0,3).设平面A1BD的法向量为n=(x,y,z),‎ ‎∴n·DB=0,‎n·DA‎1‎=0,‎即‎2‎2‎y=0,‎‎-x+3z=0,‎ ‎∴n=(3,0,1).‎ 故所求距离为d=‎‎|n·DB‎1‎|‎‎|n|‎‎=‎3‎‎10‎‎10‎.‎ ‎8.D　如图所示,以D为坐标原点,分别以DA,DC,DD1所在的直线为x,y,z轴建立空间直角坐标系,则O‎1‎‎2‎‎,‎1‎‎2‎,‎‎1‎‎2‎,B(1,1,0),E1,0,‎3‎‎4‎,F‎1‎‎2‎,1,0,则|OE|=‎1‎‎4‎‎+‎1‎‎4‎+‎‎1‎‎16‎‎=‎‎3‎‎4‎,|OB|=‎3‎‎2‎,|BE|=‎5‎‎4‎,‎ 所以cos∠BOE=‎9‎‎16‎‎+‎3‎‎4‎-‎‎25‎‎16‎‎2×‎3‎‎4‎×‎‎3‎‎2‎=-‎3‎‎9‎,‎ 所以sin∠BOE=‎78‎‎9‎,‎ 所以S△OEB=‎1‎‎2‎‎×‎3‎‎4‎×‎3‎‎2‎×‎78‎‎9‎=‎‎26‎‎16‎,‎ 设平面OEB的一个法向量为n=(x,y,z),‎ 由n·OE=‎1‎‎2‎x-‎1‎‎2‎y+‎1‎‎4‎z=0,‎n·OB=‎1‎‎2‎x+‎1‎‎2‎y-‎1‎‎2‎z=0,‎ 取z=1,得n=‎1‎‎4‎‎,‎‎3‎‎4‎,1,‎ 又BF=-‎1‎‎2‎,0,0,‎ 所以F到平面OEB的距离h=‎|n·BF|‎‎|n|‎‎=‎1‎‎8‎‎26‎‎4‎=‎‎26‎‎52‎,所以四面体OEBF的体积为V=‎1‎‎3‎S△OEB×h=‎‎1‎‎3‎‎×‎26‎‎16‎×‎26‎‎52‎=‎1‎‎96‎.‎ ‎9.0,‎1‎‎3‎　建立如图所示的空间直角坐标系,则A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,1),由D‎1‎PD‎1‎B=λ得P(λ,λ,1-λ),则PA=(1-λ,-λ,λ-1),PC=(-λ,1-λ,λ-1),因为∠APC为锐角,所以PA‎·‎PC=(1-λ,-λ,λ-1)·(-λ,1-λ,λ-1)=(λ-1)(3λ-1)>0,解得λ<‎1‎‎3‎或λ>1,又因为动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,所以λ的取值范围为0≤λ<‎‎1‎‎3‎‎.‎ ‎10.(1)证明 由题知EA⊥平面ABCD,BA⊂平面ABCD,∴BA⊥AE.过点A作AH⊥BC于H,在Rt△ABH中,∠ABH=60°,BH=‎1‎‎2‎,∴AB=1,在△ABC中,AC2=AB2+BC2-2AB·BCcos 60°=3,‎ ‎∴AB2+AC2=BC2,∴AB⊥AC,‎ 且AC∩EA=A,∴AB⊥平面ACFE.又∵CF⊂平面ACFE,∴AB⊥CF.‎ ‎(2)以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,则B(1,0,0),E(0,0,1),F0,‎3‎‎2‎,1,D-‎1‎‎2‎‎,‎‎3‎‎2‎,0,‎ ‎∴‎BE‎=(-1,0,1),BF=-1,‎3‎‎2‎,1,DE=‎1‎‎2‎,-‎3‎‎2‎,1,DF=‎1‎‎2‎,0,1.‎ 设n=(x,y,z)为平面BEF的一个法向量,则n·BE=-x+z=0,‎n·BF=-x+‎3‎‎2‎y+z=0,‎令x=1,得n=(1,0,1),同理可求平面DEF的一个法向量m=(2,0,-1),‎ ‎∴cos=m·n‎|m||n|‎‎=‎‎10‎‎10‎,‎ 所以二面角B-EF-D的余弦值为‎10‎‎10‎‎.‎ ‎11.(1)证明 ∵平面ABB1A1⊥平面ABC,BB1⊥BA,平面ABB1A1∩平面ABC=AB,‎ ‎∴BB1⊥平面ABC.‎ 又CC1⊥平面ABC,∴BB1∥CC1,‎ 又CC1=‎1‎‎2‎AB=‎1‎‎2‎BB1=BE,‎ ‎∴四边形CC1EB为平行四边形,‎ ‎∴C1E∥BC.‎ 又BC⊂平面A1BC,C1E⊄平面A1BC,∴C1E∥平面A1BC.‎ ‎∵BE=EB1,A1F=FB1,∴EF∥A1B,‎ 又A1B⊂平面A1BC,EF⊄平面A1BC,∴EF∥平面A1BC.‎ 又C1E∩EF=E,C1E⊂平面EFC1,FE⊂平面EFC1,‎ ‎∴平面EFC1∥平面A1BC.‎ ‎(2)在△ABC中,由余弦定理得:AC2=AB2+BC2-2AB·BCcos 60°=12,‎ ‎∴AB2=AC2+BC2,‎ ‎∴△ABC为直角三角形,且∠ACB=90°,‎ ‎∴AC⊥BC,由CC1⊥平面ABC可得CC1⊥AC,CC1⊥BC,‎ ‎∴CA,CB,CC1两两垂直.‎ 以C点为坐标原点,CA‎,CB,‎CC‎1‎依次为x轴,y轴,z轴正方向,建立空间直角坐标系,如下图所示,‎ 则C(0,0,0),C1(0,0,2),A1(2‎3‎,0,4),E(0,2,4λ).‎ 设平面A1EC1的一个法向量为n1=(x1,y1,z1),‎ 则n‎1‎‎·C‎1‎A‎1‎=0,‎n‎1‎‎·C‎1‎E=0,‎ 即‎2‎3‎x‎1‎+2z‎1‎=0,‎‎2y‎1‎+(4λ-2)z‎1‎=0,‎ 令z1=1,解得x1=-‎3‎‎3‎,y1=1-2λ,∴n1=-‎3‎‎3‎,1-2λ,1.‎ 设平面A1EC的一个法向量为n2=(x2,y2,z2),‎ 则n‎2‎‎·CA‎1‎=0,‎n‎2‎‎·CE=0,‎ 即‎2‎3‎x‎2‎+4z‎2‎=0,‎‎2y‎2‎+4λz‎2‎=0,‎ 令x2=2,得z2=-‎3‎,y2=2‎3‎λ,‎ ‎∴n2=(2,2‎3‎λ,-‎3‎).‎ 若平面A1EC1⊥平面A1EC,‎ 则n1·n2=-‎2‎‎3‎‎3‎+2‎3‎λ(1-2λ)-‎3‎=0,化简得12λ2-6λ+5=0,‎ 由于Δ<0,故此方程无解,所以不存在实数λ,使得平面A1EC1⊥平面A1EC.‎ ‎12.解 (1)证明:如图,取BB1中点E,连接AE,EH.‎ ‎∵H为BQ中点,∴EH∥B1Q.‎ 在平行四边形AA1B1B中,P,E分别为AA1,BB1的中点,∴AE∥PB1.‎ 又EH∩AE=E,PB1∩B1Q=B1,‎ ‎∴平面EHA∥平面B1QP.‎ ‎∵AD⊂平面EHA,‎ ‎∴AD∥平面B1PQ.‎ ‎(2)连接PC1,AC1,‎ ‎∵四边形A1C1CA为菱形,‎ ‎∴AA1=AC=A1C1=4.‎ 又∠C1A1A=60°,‎ ‎∴△AC1A1为正三角形.‎ ‎∵P为AA1的中点,∴PC1⊥AA1.‎ ‎∵平面ACC1A1⊥平面ABB1A1,平面ACC1A1∩平面ABB1A1=AA1,PC1⊂平面ACC1A1,∴PC1⊥平面ABB1A1,‎ 在平面ABB1A1内过点P作PR⊥AA1交BB1于点R,建立如图所示的空间直角坐标系P-xyz,则 P(0,0,0),A1(0,2,0),A(0,-2,0),C1(0,0,2‎3‎),C(0,-4,2‎3‎),‎ 设AQ=λAC=λ(0,-2,2‎3‎),λ∈[0,1],∴Q(0,-2(λ+1),2‎3‎λ),‎ ‎∴‎PQ‎=(0,-2(λ+1),2‎3‎λ).‎ ‎∵A1B1=AB=2,∠B1A1A=60°,‎ ‎∴B1(‎3‎,1,0),‎ ‎∴‎PB‎1‎‎=(‎3‎,1,0).‎ 设平面PQB1的法向量为m=(x,y,z),‎ 则m·PQ=0,‎m·PB‎1‎=0‎ 得‎-2(λ+1)y+2‎3‎λz=0,‎‎3‎x+y=0,‎ 令x=1,则y=-‎3‎,z=-λ+1‎λ,‎ ‎∴平面PQB1的一个法向量为m=1,-‎3‎,-λ+1‎λ,‎ 设平面AA1C1C的法向量为n=(1,0,0),二面角B1-PQ-C1的平面角为θ,则cos θ=m·n‎|m||n|‎‎=‎1‎‎1+3+(-λ+1‎λ)‎‎ ‎‎2‎=‎‎13‎‎13‎,∴λ=‎1‎‎2‎或λ=-‎1‎‎4‎(舍),‎ ‎∴AQ=‎‎1‎‎2‎AC‎,∴Q(0,-3,‎3‎).‎ 又B(‎3‎,-3,0),‎∴‎QB=(‎3‎,0,-‎3‎),‎ ‎∴|QB|=‎‎3+3‎‎=‎6‎.‎ 又B1Q=‎22‎,∴B1Q2=BQ2+BB‎1‎‎2‎,即△BB1Q是直角三角形,∠B1BQ=90°.连接BP,设点P到平面BQB1的距离为h,则‎1‎‎3‎‎×‎1‎‎2‎×‎4‎×‎3‎×‎3‎=‎1‎‎3‎×‎1‎‎2‎×‎4‎×‎6‎×‎h,‎ ‎∴h=‎6‎‎2‎,即点P到平面BQB1的距离为‎6‎‎2‎‎.‎ ‎13.解 (1)证法一:∵AB⊥AD,且AB=AD=2,∴BD=2‎2‎,‎ 又△PBD为正三角形,所以PB=PD=BD=2‎2‎,‎ 又∵AB=2,PA=2‎3‎,所以AB⊥PB,‎ 又∵AB⊥AD,BC∥AD,‎ ‎∴AB⊥BC,PB∩BC=B,‎ 所以AB⊥平面PBC,又因为AB⊂平面PAB,所以平面PAB⊥平面PBC.‎ 证法二:设P在平面ABCD内的射影为Q,连接AQ,则AQ即为AP在平面ABCD内的射影,故∠PAQ即为AP与底面所成的角,因为tan∠PAQ=‎2‎‎2‎,‎ 所以sin∠PAQ=‎‎3‎‎3‎‎.‎ 而sin∠PAQ=PQPA,AP=2‎3‎,‎ 所以PQ=2,AQ=2‎‎2‎‎.‎ 又△PBD为正三角形,‎ 所以PB=PD=BD=2‎2‎,‎ 所以DQ=2.‎ 由AD=DQ=2,AQ=2‎2‎,得AD⊥DQ,所以AB