2018届二轮复习4-4函数y=Asin(ωxφ)的图象及应用课件（全国通用）

2018届二轮复习4-4函数y=Asin(ωxφ)的图象及应用课件（全国通用）

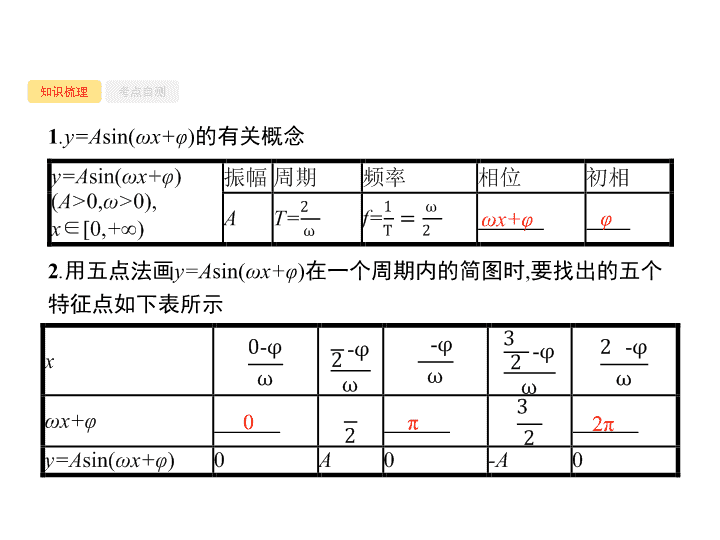
4 . 4 　 函数 y=A sin( ωx+φ ) 的图象 及应用 - 2 - - 3 - 知识梳理 考点自测 1 .y=A sin( ω x+ φ ) 的有关概念 2 . 用五点法画 y=A sin( ω x+ φ ) 在一个周期内的简图时 , 要找出的五个特征点如下表所示 ω x+ φ φ 0 π 2 π - 4 - 知识梳理 考点自测 3 . 由 y= sin x 的图象得 y=A sin( ω x+ φ )( A> 0, ω > 0) 的图象的两种方法 | φ | - 5 - 知识梳理 考点自测 y=A sin( ω x+ φ )( A> 0, ω > 0) 的图象的作法 : (1) 五点法 : 用 “ 五点法 ” 作 y=A sin( ω x+ φ ) 的简图 , 主要是通过变量代换 , 设 z= ω x+ φ , 由 z 取 来求出相应的 x , 通过列表 , 计算得出五点坐标 , 描点后得出图象 . (2) 图象变换法 : 由函数 y= sin x 的图象通过变换得到 y=A sin( ω x+ φ ) 的图象 , 有两种主要途径 “ 先平移后伸缩 ”( 即 “ 先 φ 后 ω ”) 与 “ 先伸缩后平移 ”( 即 “ 先 ω 后 φ ”) . - 6 - 知识梳理 考点自测 × √ × × × - 7 - 知识梳理 考点自测 D - 8 - 知识梳理 考点自测 D - 9 - 知识梳理 考点自测 6 - 10 - 考点一 考点二 考点三 函数 y=A sin( ω x+ φ ) 的图象及变换 - 11 - 考点一 考点二 考点三 - 12 - 考点一 考点二 考点三 - 13 - 考点一 考点二 考点三 思考 作函数 y=A sin( ω x+ φ )( A> 0, ω > 0) 的图象有哪些方法 ? 解题心得 1 . 函数 y=A sin( ω x+ φ )( A> 0, ω > 0) 的图象的两种作法 : (1) 五点法 : 用 “ 五点法 ” 作 y=A sin( ω x+ φ ) 的简图 , 主要是通过变量代换 , 设 z= ω x+ φ , 由 z 取 来求出相应的 x , 通过列表 , 计算得出五点坐标 , 描点后得出图象 . (2) 图象变换法 : 由函数 y= sin x 的图象通过变换得到 y=A sin( ω x+ φ ) 的图象 , 有两种主要途径 “ 先平移后伸缩 ” 与 “ 先伸缩后平移 ” . 2 . 变换法作图象的关键是看 x 轴上是先平移后伸缩还是先伸缩后平移 , 对于后者可利用 来确定平移单位 . - 14 - 考点一 考点二 考点三 - 15 - 考点一 考点二 考点三 - 16 - 考点一 考点二 考点三 - 17 - 考点一 考点二 考点三 - 18 - 考点一 考点二 考点三 求函数 y=A sin( ω x+ φ ) 的解析式 ( 多考向 ) 考向 1 　 由函数的图象求函数 y=A sin( ω x+ φ ) 的解析式 例 2 函数 y=A sin( ω x+ φ ) 的部分图象如图所示 , 则 ( 　　 ) A - 19 - 考点一 考点二 考点三 思考 由 y=A sin( ω x+ φ ) +b ( A> 0, ω > 0) 的图象求其解析式的方法和步骤是怎样的 ? - 20 - 考点一 考点二 考点三 考向 2 　 由函数 y=A sin( ω x+ φ ) 的性质求解析式 - 21 - 考点一 考点二 考点三 思考 如何由函数 y=A sin( ω x+ φ ) 的性质确定 A , ω , φ ? - 22 - 考点一 考点二 考点三 - 23 - 考点一 考点二 考点三 - 24 - 考点一 考点二 考点三 - 25 - 考点一 考点二 考点三 - 26 - 考点一 考点二 考点三 函数 y=A sin( ω x+ φ ) 性质的应用 - 27 - 考点一 考点二 考点三 - 28 - 考点一 考点二 考点三 - 29 - 考点一 考点二 考点三 思考 如何求解三角函数图象与性质的综合问题 ? 解题心得 解决三角函数图象与性质综合问题的方法 : 先将 y=f ( x ) 化为 y=a sin x+b cos x 的形式 , 再用辅助角公式化为 y=A sin( ω x+ φ ) 的形式 , 最后借助 y=A sin( ω x+ φ ) 的性质 ( 如周期性、对称性、单调性等 ) 解决相关问题 . - 30 - 考点一 考点二 考点三 - 31 - 考点一 考点二 考点三 - 32 - 考点一 考点二 考点三 1 . 由函数 y=A sin( ω x+ φ ) 的图象确定 A , ω , φ 的题型 , 常常以 “ 五点法 ” 中的五个点作为突破口 , 要从图象的升降情况找准第一个 “ 零点 ” 和第二个 “ 零点 ” 的位置 . 要善于抓住特殊量和特殊点 . 2 . 函数 y=A sin( ω x+ φ ) 的图象与 x 轴的每一个交点均为其对称中心 , 若函数 f ( x ) =A sin( ω x+ φ ) 的图象关于点 ( x 0 ,0) 成中心对称 , 则 ω x 0 + φ =k π ( k ∈ Z ); 经过函数 y=A sin( ω x+ φ ) 图象的最高点或最低点 , 且与 x 轴垂直的直线都为其对称轴 , 两个相邻对称轴的距离是半个周期 . 若函数 f ( x ) =A sin( ω x+ φ ) 的图象关于直线 x=x 0 对称 , 则 ω x 0 + φ =k π + ( k ∈ Z ) . - 33 - 考点一 考点二 考点三 1 . 在三角函数的平移变换中 , 无论是先平移再伸缩 , 还是先伸缩再平移 , 只要平移 | φ | 个单位 , 都是相应的解析式中的 x 变为 x ± | φ |. 2 . 函数 y=A sin( ω x+ φ )( A> 0, ω > 0) 的单调区间的确定 , 基本思想是把 ( ω x+ φ ) 看作一个整体 , 若 ω < 0, 则要根据诱导公式转化成 ω > 0 .