- 2021-06-12 发布 |
- 37.5 KB |
- 15页

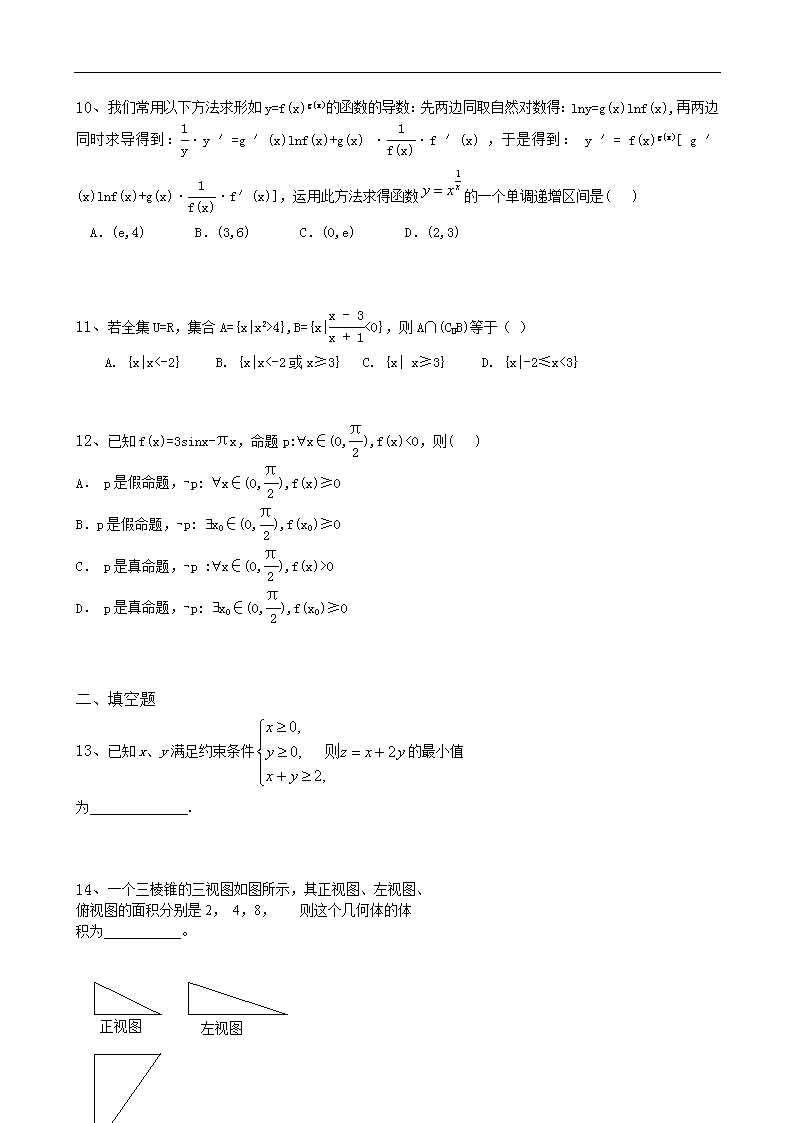
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁省葫芦岛市 2012年高三第三次联合模拟考试
辽宁省葫芦岛市 2012年高三第三次联合模拟考试 一、选择题 1、F(-c,0)是双曲线-=1(a>0,b>0)的左焦点,P是抛物线y2=4cx上一点,直线FP与圆x2+y2=a2相切于点E,且PE=FE,若双曲线的焦距为2+2,则双曲线的实轴长为( ) (A)4 (B)2 (C) (D) 2、已知x,y∈R,i为虚数单位,且(x-1)i+y=2+i,则(1+i)x+y的值为( ) A .4 B.-4 C .4+4i D.2i 3、袋中有6个小球,分别标有数字1,2,3,4,5,6,甲乙两人玩游戏,先由甲从袋中任意摸出一个小球,记下号码a后放回袋中,再由乙摸出一个小球,记下号码b,若|a-b|≤1,就称甲乙两人“有默契”,则甲乙两人“有默契”的概率为( ) A. B. C. D. 4、执行如图所示的程序框图,若输入x=3,则输出y的值为( ) A.5 B.9 C.17 D.33 开始 y=2x-1 1 输出y 结束 是 x=y 否 输入x |x-y|>8 5、球O为长方体ABCD-A1B1C1D1的外接球,已知AB=2,AD=, AA1=,则顶点A、B间的球面距离是( ) A. B. C. D. 6、已知函数y=Asin(ωx+φ)(ω>0,|φ|<)的简图如下图,则 的值为( ) A. B. C. - D. - 2 -1 y x 7、已知公比不为1的等比数列的首项为1, 若3a1,2a2,a3成等差数列,则数列 的前5项和为( A ) A. B. C. 121 D. 31 8、已知椭圆+=1(a>b>0)的右焦点为F,离心率为,过点F且倾斜角为60°的直线l与椭圆交于A、B两点(其中A点在x轴上方),则的值等于( ) A.2 B. C. D. 9、在边长为4的正方形ABCD中,E为BC中点,P为DE中点,则·的值为( ) A.-5 B.-4 C.4 D.5 10、我们常用以下方法求形如y=f(x)g(x)的函数的导数:先两边同取自然对数得:lny=g(x)lnf(x),再两边同时求导得到:·y′=g′(x)lnf(x)+g(x)··f′(x),于是得到: y′= f(x)g(x)[ g′(x)lnf(x)+g(x)··f′(x)],运用此方法求得函数的一个单调递增区间是( ) A.(e,4) B.(3,6) C.(0,e) D.(2,3) 11、若全集U=R,集合A={x|x2>4},B={x|<0},则A∩(CUB)等于( ) A. {x|x<-2} B. {x|x<-2或x≥3} C. {x| x≥3} D. {x|-2≤x<3} 12、已知f(x)=3sinx-πx,命题p:"x∈(0,),f(x)<0,则( ) A. p是假命题,Øp: "x∈(0,),f(x)≥0 B.p是假命题,Øp: $x0∈(0,),f(x0)≥0 C. p是真命题,Øp :"x∈(0,),f(x)>0 D. p是真命题,Øp: $x0∈(0,),f(x0)≥0 二、填空题 13、已知x、y满足约束条件的最小值 为 . 14、一个三棱锥的三视图如图所示,其正视图、左视图、 俯视图的面积分别是2, 4,8, 则这个几何体的体 积为___________。 正视图 左视图 俯视 15、已知an=,数列{}的前n项和为Sn,bn=n-33,n∈N*,则bnSn的最小值为__________. 16、(1+2x2)(x-)8的展开式中常数项是________(用数字作答); 三、解答题 17、 已知函数f(x)=|x-2|-|x+1|. (Ⅰ)若f(x)≤a恒成立,求a的取值范围;(Ⅱ)解不等式f(x)≥x2-2x. 18、 已知△ABC的三个内角A,B,C所对的边分别是a,b,c,且=- (Ⅰ)求角B的值; (Ⅱ)若b=,a+c=4,求△ABC的面积. 19、 在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=CD=a. (1)求证:面PAD⊥面PAC; (2)求二面角D-PB-C的余弦值; (3)求点D到平面PBC的距离; P A B C D 20、 根据辽宁省期初教育工作会议精神,我省所有中小 学全部取消晚自习,某校高二年级共有学生1000名, 其中走读生750名,住宿生250名,现从该年级采用 分层抽样的方法从该年级抽取n名学生进行问卷调 查.根据问卷取得了这n名同学每天晚上有效学习时 间(单位:分钟)的数据,按照以下区间分为八组 ①[0,30),②[30,60),③[60,90),④[90,120), ⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240), 得到频率分布直方图如下.已知抽取的学生中每天晚上 有效学习时间少于60分钟的人数为5人; (1)求n的值并补全下列频率分布直方图; (2)如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的n名学生,完成下列2×2列联表: 利用时间充分 利用时间不充分 总计 走读生 50 25 75 住宿生 10 15 25 总计 60 40 100 是否有95%的把握认为学生利用时间是否充分与走读、住宿有关? (3)若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因,记抽到“有效学习时间少于60分钟”的学生人数为X,求X的分布列及期望; 参考公式:K2= 时间(分钟) 频率/组距 1/3000 0 90 120 150 30 60 180 210 240 1/600 1/300 1/750 1/200 1/100 21、如图,椭圆C:+=1(a>b>0)的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6 (1)求椭圆C的方程; (2)设直线AF1与椭圆交于另一点B,与y轴交于一点C,记m=,n=,若点A在第一象限,求m+n的取值范围; x y A1 A2 F1 F2 A B C O 22、 已知函数f(x)=x3-2x2+bx+a,g(x)=ln(1+2x)+x (1)求f(x)的单调区间。 (2)若f(x)与g(x)有交点,且在交点处的切线均为直线y=3x,求a,b的值并证明:在公共定义域内恒有f(x)≥g(x). (3)设A(x1,g(x1)),B(x2,g(x2)),C(t,g(t))是y=g(x)图象上任意三点,且-查看更多