- 2021-06-11 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届江西省西路片区七校高三第一次联考(2017
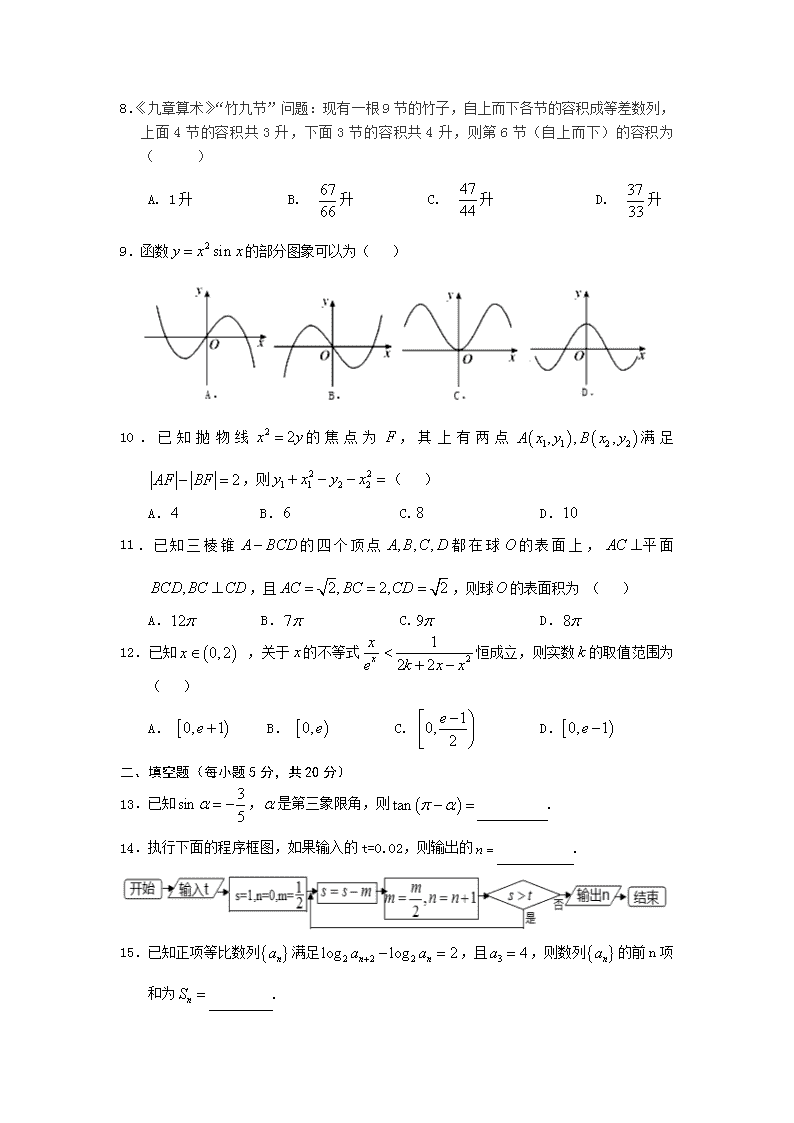
江西省西路片七校2018届高三第一次联考 数学试题(文科) 命题:井冈山中学 肖萃鹏 审题:任弼时中学 李忠华 一、选择题(每小题5分,共60分) 1.已知集合,则( ) A.[-2,1] B. [-1,1] C. [-2,3] D.[1,3] 2.复数在复平面上对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.“”是“”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.即不充分也不必要条件 4.将函数的图象向右平移个单位,得到函数的图象,则( ) A. B. C. D.0 5.已知向量,若间的夹角为,则( ) A. B. C. D. 6.某同学在研究性学习中,收集到某制药厂今年前个月甲胶囊生产产量(单位:万盒)的数据如下表所示: (月份) (万盒) 若线性相关,线性回归方程为,估计该制药厂月份生产甲胶囊产量为( ) A.万盒 B.万盒 C.万盒 D.万盒 7.实数满足条件,则目标函数的最大值为( ) A. B.7 C. D. 8.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第6节(自上而下)的容积为( ) A. 1升 B. 升 C. 升 D. 升 9.函数的部分图象可以为( ) 10.已知抛物线的焦点为,其上有两点满足,则( ) A. B. C. D. 11.已知三棱锥的四个顶点都在球的表面上,平面,且,则球的表面积为 ( ) A. B. C. D. 12.已知 ,关于的不等式恒成立,则实数的取值范围为( ) A. B. C. D. 二、填空题(每小题5分,共20分) 13.已知,是第三象限角,则 . 14.执行下面的程序框图,如果输入的t=0.02,则输出的 . 15.已知正项等比数列满足,且,则数列的前n项和为 . 16.已知且,函数,其中,则函数 的最大值与最小值之和为 . 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) 已知是递增的等差数列,,是方程的根。 (I)求的通项公式; (II)求数列的前项和. 18.(本小题满分12分) 已知向量,函数. (I)求函数的最小正周期及值域; (II)已知中,角、、所对的边分别为、、,若,求的周长. 19.(本小题满分12分) 某省重点高中2018届高三文科名学生参加了9月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取名学生的成绩进行统计分析,抽出的名学生的数学、语文成绩如下表. 语 文 优 良 及格 数 学 优 8 m 9 良 9 n 11 及格 8 9 11 (Ⅰ)将学生编号为:001,002,003,……499,500,若从第行第6列的数开始右读,请你依次写出最先抽出的 个人的编号(下面是摘自随机用表的第四行至第七行) 12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76 55 59 56 35 34 34 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 (Ⅱ)若数学优秀率为,求的值; (Ⅲ)在语文成绩为良的学生中,已知,求数学成绩“优”比“良”的人数少的概率. 20.(本小题满分12分) 如图,四棱锥P—ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点. (Ⅰ)求证:PC⊥AD; (Ⅱ)求点D到平面PAM的距离. 21.(本小题满分12分) 已知椭圆和圆分别与射线交于两点,且. (Ⅰ)求椭圆的方程; (Ⅱ)若不经过原点且斜率为的直线与椭圆交于两点,且,证明:线段中点的坐标满足. 22.(本小题满分12分) 已知函数. (Ⅰ)若,求函数的在处的切线方程; (Ⅱ) 若,证明:方程无解. 2018届西路片七校高三文科数学联考答案 一、选择题: 1. C 2.D 3.A 4.C 5.A 6.C 7.B 8. D 9.A 10.B 11.D 12.C 二、填空题 13、 14、6 15、2n_1 16、4 三、解答题 17.解:(Ⅰ)方程的两根为2,3,由题意得 设数列的公差为d,则故从而 所以的通项公式为 ……5分 (II)设的前n项和为由(I)知则 两式相减得所以 ……10分 18. (Ⅰ)由题,,所以 的最小正周期为,,故的值域为.……6分 (Ⅱ),又,得.在中,由余弦定理,得,又,所以,所以的周长为.……………………12分 19.解析:(Ⅰ)编号依次为:.………………3分 (Ⅱ)由,得,因为, 得.………………6分 (Ⅲ)由题意且,所以满足条件的有,共种,且每组出现都是等可能的.记: “数学成绩“优”比“良”的人数少” 为事件,则事件包含的基本事件有,共种,所以.………………12分 20.(Ⅰ)取AD中点O,连结OP,OC,AC,依题意可知△PAD,△ACD均为正三角形, ∴OC⊥AD,OP⊥AD,又OC∩OP=O,OC⊂平面POC,OP⊂平面POC, ∴AD⊥平面POC,又PC⊂平面POC,∴PC⊥AD.………………4分 (Ⅱ)点D到平面PAM的距离即点D到平面PAC的距离, 由(Ⅰ)可知PO⊥AD,又平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD,PO⊂平面PAD, ∴PO⊥平面ABCD,即PO为三棱锥P﹣ACD的体高. ∴△PAC的面积, 设点D到平面PAC的距离为h,由VD﹣PAC=VP﹣ACD得, 又,∴, 解得,∴点D到平面PAM的距离为. ……………………12分 21.(Ⅰ)由,知圆半径为,由,知,设,则,椭圆的方程为. ………………4分 (Ⅱ)设,设直线的方程为,由,得,所以,………7分,而,原点到直线的距离为,所以,所以,即,即,则 ,① ,② 由①,②消去得.…………12分 22. (Ⅰ)依题意,,故,故所求切线方程为………………4分 (Ⅱ)依题意,,即,即,令,当时,,令,得,令,得,所以函数在单调递增;令,得,所以函数在单调递减,所以,所以.………………8分 设,所以,令,得,所以函数在单调递增;令,得,所以函数在单调递减,所以,即,所以,即,所以方程无解.………………12分查看更多