- 2021-06-11 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
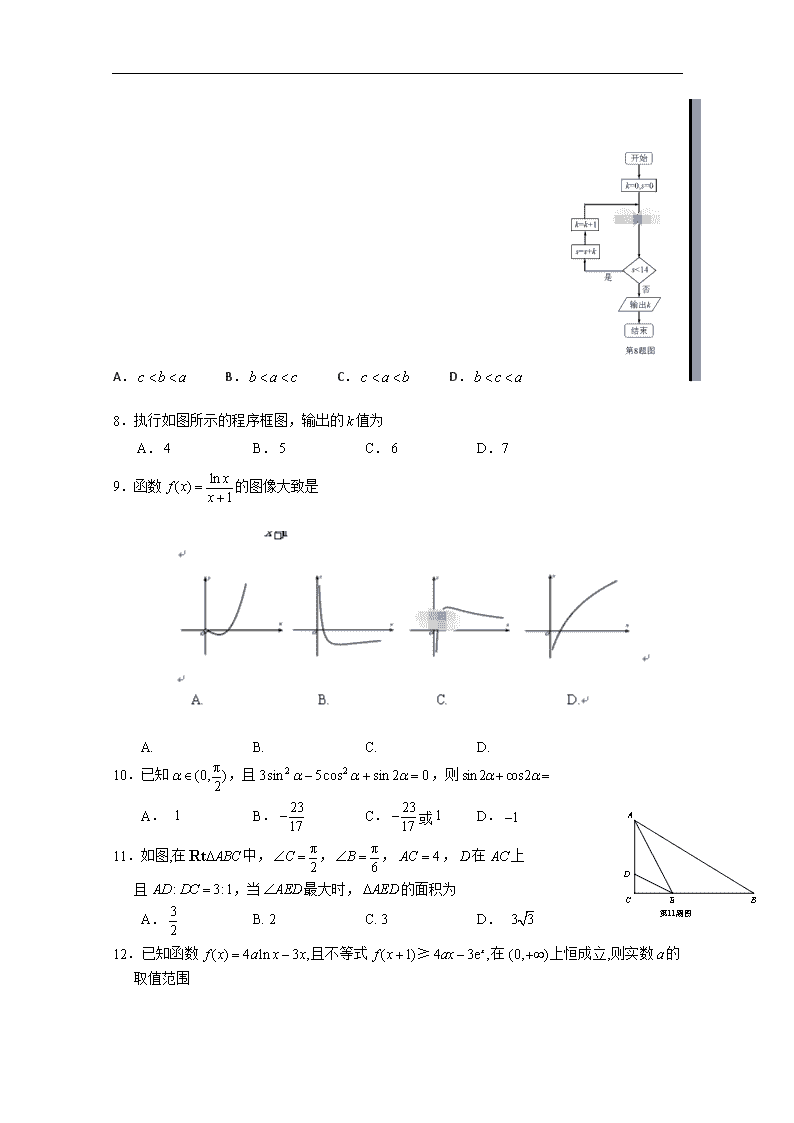
四川省宜宾市2020届高三上学期一诊考试数学(文)试卷 含答案
www.ks5u.com 文科数学 注意事项: 1. 答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。 2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。 3. 考试结束后,将答题卡交回。 一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合要求的。 1.已知集合,,则 A. B. C. D. 2.已知是虚数单位,复数在复平面内对应的点在第二象限,则实数的取值范围是 A. B. C. D. 3.已知向量,且,则实数 A. B. C. D. 4.某车间生产三种不同型号的产品,产量之比分别为,为检验产品的质量,现用分层抽样的方法抽取一个容量为的样本进行检验,已知种型号的产品共抽取了件,则种型号的产品抽取的件数为 A. B. C. D. 5.要得到函数的图象,只需要将函数的图象 A.向左平行移动个单位长度,横坐标缩短为原来的倍,纵坐标不变. B.向左平行移动个单位长度,横坐标缩短为原来的倍,纵坐标不变. C.向右平行移动个单位长度,横坐标伸长为原来的倍,纵坐标不变. D.向右平行移动个单位长度,横坐标伸长为原来的倍,纵坐标不变. 6.设直线是两条不同的直线,是两个不同的平面,下列命题中正确的是 A. B. C. D. 7.已知,则 A. B. C. D. 8.执行如图所示的程序框图,输出的值为 A. B. C. D.7 9.函数的图像大致是 A. B. C. D. 10.已知,且,则 A. B. C.或 D. 11.如图,在中,,,,在上 且,当最大时,的面积为 A. B. C. D. 12.已知函数且不等式在上恒成立,则实数的取值范围 A. B. C. D. 二、填空题:本大题共4个小题,每小题5分,共20分。 13.书架上有本不同的数学书,本不同的英语书,从中任意取出本,取出的书恰好是数学书的概率是 . 14.已知函数在处取得极值,则实数 . 15.若的内角A、B、C的对边分别为a、b、c,其面积为,, 则 . 16.同学们有如下解题经验:在某些数列求和中,可把其中一项分裂为两项之差,使某些项可以抵消,从而实现化简求和.如:已知数列的通项,则将其通项化为,故数列的前项的和.斐波那契数列是数学史上一个著名数列,在斐波那契数列中,,,若,那么 . 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。 (一)必考题:共60分. .(12分) 已知数列的前项和为,满足. (1)求数列的通项公式; (2)设,求数列的前项和. .(12分) 在中,分别为内角的对边,且满足. (1)若,,求; (2)若,,求的面积. .(12分) 手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图: (1)求直方图中的值,并由频率分布直方图估计该单位职工一天步行数的中位数; (2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数; (3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间的概率. 20.(12分) 如图,正方形的边长为,点E是边的中点,将沿翻折得到,且平面平面. (1)求三棱锥的体积; (2)设线段上一点满足,在上是否存在点使平面?若存在,求出的长度;若不存在,说明理由. .(12分) 已知函数. (1)若函数在区间内单调递增,求实数的取值范围; (2)若,且,证明:. (二)选考题:共10分。请考生在第22、23题中选一题作答。如果多做,则按所做的第一题计分。 22.(10分)[选修4-4:坐标系与参数方程] 如图所示,“”是在极坐标系中分别以和为圆心,外切于点的两个圆.过作两条夹角为的射线分别交于O、A两点,交于O、B两点. (1)写出与的极坐标方程; (2)求面积最大值. 23.(10分)[选修4-5:不等式选讲] 已知函数,. (1),有,求实数的取值范围; (2)若不等式的解集为,正数a、b满足,求的最小值. (文史类)数学试题参考答案 说明: 一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则. 二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分. 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A D C B B D C C A C B 二、填空题 13. 14.6 15. 16. 三、解答题 17.解:(1)∵,当时, 当时 , 两式相减得 当时,满足通项. ∴是以首项为,公比为的等比数列 ( ) ..........6分 (2)由(1)知 两式相减得 ....................12分 18.解:(1) , ,则, 由正弦定理得,,即, 联立,得 …………………………………………………………………6分 (2)由余弦定理可得,,即 得 ,则 …………………………………………12分 19.解:(1)由题意得 解得 设中位数为,则 解得 ∴中位数是 ........................................... 4分 (2)由 ∴估计职工一天步行数不大于步的人数为人 ........................................... 6分 (3) 在区间中有人 在区间中有人 在区间中有人 按分层抽样抽取6人,则从抽取4人,抽取1人抽取1 人. ...... 8分 设从抽取职工为,从抽取职工为,从抽取职工为,则从6人中抽取2人的情况有共15种情况,它们是等可能的,其中满足两人均来自区间的有共有6种情况, ∴两人均来自区间的概率为. ...... 12分 20.解:(1)过作于∵平面平面交线为 ∴平面. 在中 由得 . ∴三棱锥的体积..........6分 (2) 连接交于,连接 ∵ ∴∽ 又∵ .. 又平面 平面 平面 此时 ...............................12分 21.解:(1)的定义域是, , 若函数在区间递增, 则有在内恒成立, 即恒成立, 又函数在时取得最小值,故; ..................6分 (2)要原不等式成立, 只要成立即可, 令,故只要即可, 由(1)可知函数在递增, 故, 故成立. ..................12分 22.解:(1);; (2)由(I)得, 23.解(1)解:(1)由,得恒成立 ,在时恒成立 的取值范围是......................................................................................5分 方法二:根据函数的图像,找出的最小值 (2) 由得 解得 解得 将带入,整理得 当且仅当,即时取等号 ...................................................................................................10分查看更多