高考数学一轮复习练案11第二章函数导数及其应用第八讲函数的图象含解析
[练案11]第八讲 函数的图象
A组基础巩固
一、单选题
1.函数y=-ex的图象( D )
A.与y=ex的图象关于y轴对称
B.与y=ex的图象关于坐标原点对称
C.与y=e-x的图象关于y轴对称
D.与y=e-x的图象关于坐标原点对称
[解析] 由点(x,y)关于原点的对称点是(-x,-y),可知D正确.故选D.
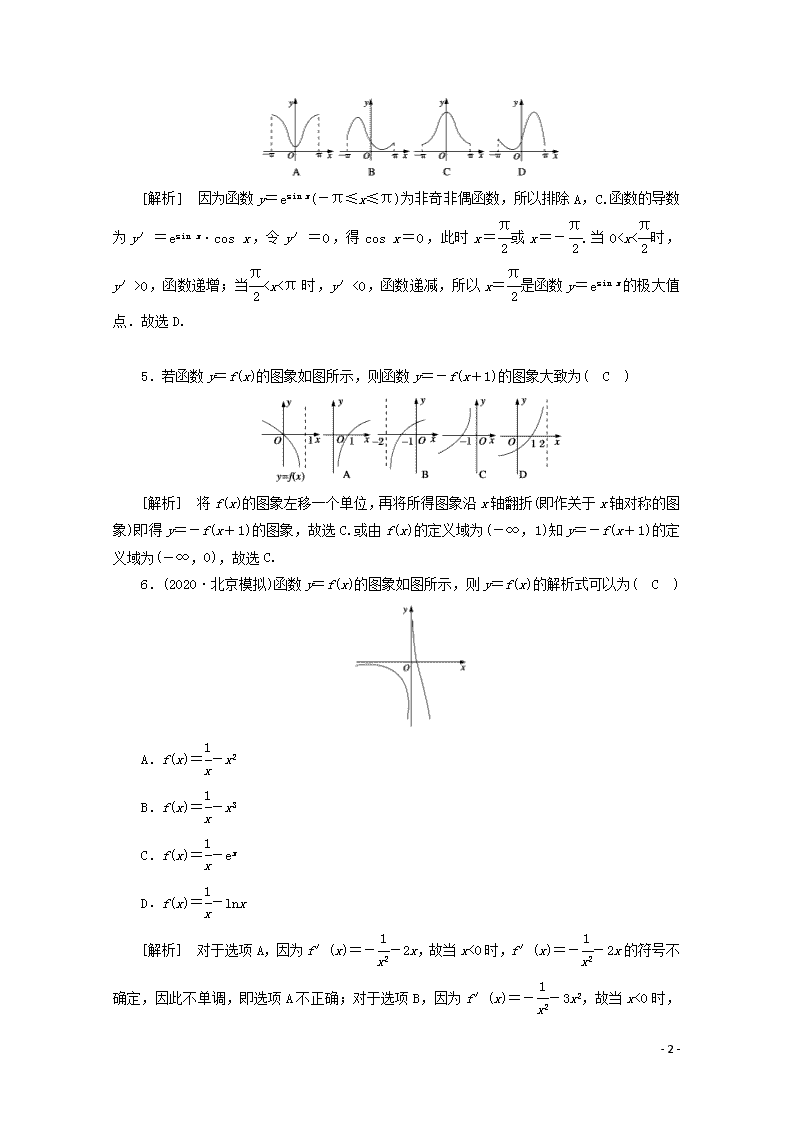
2.若函数f(x)=的图象如图所示,则f(-3)等于( C )
A.- B.-
C.-1 D.-2
[解析] 由图象可知:a(-1)+b=3,ln(-1+a)=0,所以a=2,b=5,f(x)=所以f(-3)=2×(-3)+5=-1.
3.(2020·河北高三模拟)为了得到函数y=log2的图象,可将函数y=log2x的图象上所有的点( A )
A.纵坐标缩短到原来的,横坐标不变,再向右平移1个单位
B.横坐标缩短到原来的,纵坐标不变,再向左平移1个单位
C.横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位
D.纵坐标伸长到原来的2倍,横坐标不变,再向左平移1个单位
[解析] y=log2=log2(x-1)=log2(x-1),由y=log2x的图象纵坐标缩短到原来的,横坐标不变,可得y=log2x的图象,再向右平移1个单位,可得y=log2(x-1)的图象,也即y=log2的图象.故选A.
4.(2020·山西吕梁模拟)函数y=esin x(-π≤x≤π)的大致图象为( D )
- 7 -
[解析] 因为函数y=esin x(-π≤x≤π)为非奇非偶函数,所以排除A,C.函数的导数为y′=esin x·cos x,令y′=0,得cos x=0,此时x=或x=-.当0
0,函数递增;当0,故D不正确;对于选项C,f′(x)=--ex<0,故函数在x<0时,是单调递减函数,当x>0时,函数也是单调递减函数,故C选项符合.
7.(2020·浙江杭州高级中学模拟)已知函数f(x)=logax(00时,y=f(|x|+1)=f(x+1),其图象由函数f(x)的图象向左平移1个单位得到,又函数y=f(|x|+1)为偶函数,所以再将函数y=f(x+1)(x>0)的图象关于y轴对称翻折到y轴左边,得到x<0时的图象,故选A.
二、多选题
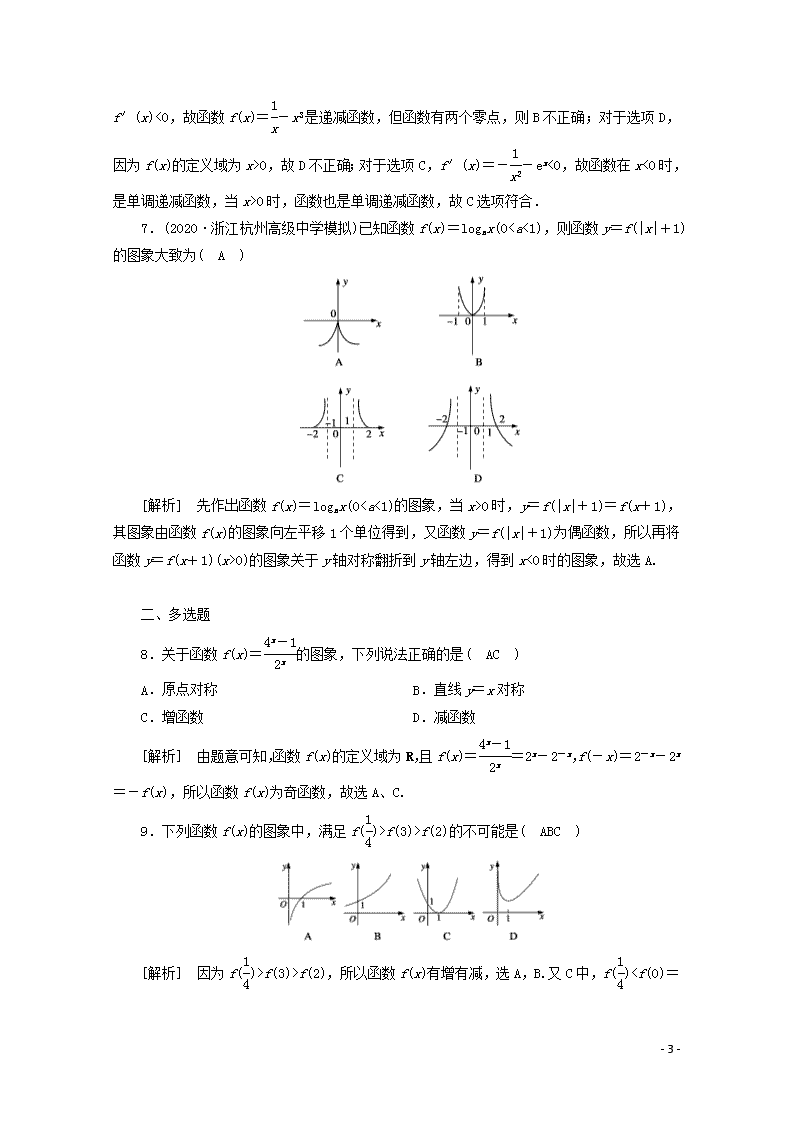
8.关于函数f(x)=的图象,下列说法正确的是( AC )
A.原点对称 B.直线y=x对称
C.增函数 D.减函数
[解析] 由题意可知,函数f(x)的定义域为R,且f(x)==2x-2-x,f(-x)=2-x-2x=-f(x),所以函数f(x)为奇函数,故选A、C.
9.下列函数f(x)的图象中,满足f()>f(3)>f(2)的不可能是( ABC )
[解析] 因为f()>f(3)>f(2),所以函数f(x)有增有减,选A,B.又C中,f()f(0),即f()0 B.c<0
C.b>0 D.a<0
[解析] 由函数图象可知,当x=0时,f(0)=>0,所以b>0;渐近线方程为x=-c,-c>0,即c<0;当x<0时,由f(x)>0恒成立可知a<0.故选B、C、D.
三、填空题
11.函数y=f(x)在x∈[-2,2]上的图象如图所示,则当x∈[-2,2]时,f(x)+f(-x)=__0__.
[解析] 由题图可知函数f(x)为奇函数,所以f(x)+f(-x)=0.
12.(2020·石家庄模拟)若函数y=f(x)的图象过点(1,1),则函数y=f(4-x)的图象一定经过点__(3,1)__.
[解析] 由于函数y=f(4-x)的图象可以看作y=f(x)的图象先关于y轴对称,再向右平移4个单位长度得到.点(1,1)关于y轴对称的点为(-1,1),再将此点向右平移4个单位长度,可推出函数y=f(4-x)的图象过定点(3,1).
13.(2019·北京西城区期末)已知函数f(x)的部分图象如图所示,若不等式-20时,y′>0,函数单调递增,所以函数④y=x·2x对应的是第二个函数图象;又当x>0时,函数③y=x·|cos x|≥0,对应的是第四个函数图象,从而排除选项B,选A.
2.(2020·安徽宿州第一次教学质量检测)函数y=(其中e为自然对数的底数)的大致图象是( B )
[解析] 解法一:由函数y=可知,当x=0时,y=0,排除C;当x<0时,y<0,排除A;
y′==,
- 7 -
当x<3时,y′>0,当x>3时,y′<0,
∴函数在(0,+∞)上先增后减.故选B.
解法二:由函数y=可知,当x=0时,y=0,排除C;
当x<0时,y<0,排除A;当x→+∞时,y→0.故选B.
3.已知函数y=f(x)和函数y=g(x)的图象,则函数y=f(x)·g(x)的部分图象可能是( A )
[解析] 由图可知y=f(x)·g(x)的定义域为(-∞,0)∪(0,+∞),排除C、D,又当x∈(0,)时,y<0,排除B,故选A.
4.(2020·湖北、山东部分重点中学第一次联考,10)已知函数y=f(x)(x∈R)满足f(x+2)=f(-x),若函数y=e|x-1|的图象与函数y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),则x1+x2+…+xn=( B )
A.0 B.n
C.2n D.4n
[解析] y=f(x)与y=e|x-1|的图象均关于直线x=1对称,由对称性,可知x1+x2+…+xn=n,故选B.
5.(2020·3月份北京市高考适应性测试)函数f(x)的定义域为 [-1,1) ,其图象如图所示.函数g(x)是定义域为R的奇函数,满足g(2-x)+g(x)=0,且当x∈(0,1)时,g(x)=f(x).给出下列三个结论:
①g(0)=0;
②函数g(x)在(-1,5)内有且仅有 3 个零点;
③不等式f(-x)<0的解集为{x|-1
查看更多