2018届二轮复习三角函数的图象和性质课件(21张)(全国通用)
三角函数的图象和性质
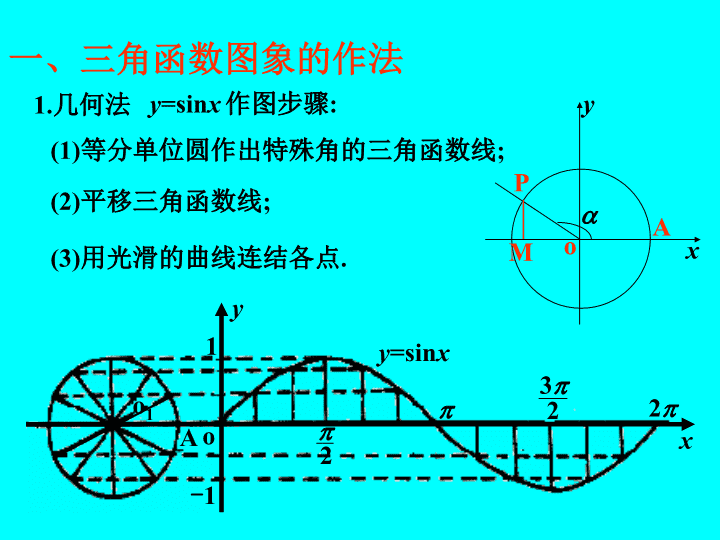
一、三角函数图象的作法
1.
几何法
y
=sin
x
作图步骤
:
(2)
平移三角函数线
;
(3)
用光滑的曲线连结各点
.
(1)
等分单位圆作出特殊角的三角函数线
;
x
y
o
P
M
A
x
y
o
y
=sin
x
-
1
1
o
1
A
2
2
3
2
2.
五点法作函数
y
=Asin(
x
+
)
的图象的步骤
:
(1)
令相位
x
+
=0, ,
, , 2
,
解出相应的
x
的值
;
2
3
2
(3)
用光滑的曲线连结
(2)
中五点
.
(2)
求
(1)
中
x
对应的
y
的值
,
并描出相应五点
;
3.
变换法
:
函数
y
=Asin(
x
+
)+
k
与
y
=sin
x
图象间的关系
:
①
函数
y
=sin
x
的图象纵坐标不变
,
横坐标向左
(
>0)
或向右
(
<0)
平移
|
|
个单位得
y
=sin(
x
+
)
的图象
;
②
函数
y
=sin(
x
+
)
图象的纵坐标不变
,
横坐标变为原来的
,
得到函数
y
=sin(
x
+
)
的图象
;
1
③
函数
y
=sin(
x
+
)
图象的横坐标不变
,
纵坐标变为原来的
A
倍
,
得到函数
y
=Asin(
x
+
)
的图象
;
④
函数
y
=Asin(
x
+
)
图象的横坐标不变
,
纵坐标向上
(
k
>0)
或向下
(
k
<0)
平移
|
k
|
个单位得
y
=Asin(
x
+
)+
k
的图象
.
要
特别注意
,
若由
y
=sin(
x
)
得到
y
=sin(
x
+
)
的图象
,
则向左或向右平移应平移
|
|
个单位
.
二、三角函数图象的性质
注
正
切
函数的对称中心有两类
:
一类是图象与
x
轴的交点
,
另一类是渐近线与
x
轴的交点
,
但无对称轴
,
这是与正弦、余弦函数的不同之处
.
1.
正弦函数
y
=sin
x
(
x
R
)
是奇函数
,
对称中心是
(
k
, 0)
(
k
Z),
对称轴是直线
x
=
k
+
(
k
Z
)
;
余弦函数
y
=cos
x
(
x
R
)
是偶函数
,
对称中心是
(
k
+
, 0)
(
k
Z),
对称轴是直线
x
=
k
(
k
Z
)
(
正
,
余
弦函数的对称轴为过最高点或最低点且垂直于
x
轴的直线
,
对称中心为图象与
x
轴的交点
)
.
2
2
2.
正切函数
y
=tan
x
(
x
R
,
x
+
k
,
k
Z
)
是奇函数
,
对称中心是
(
, 0)(
k
Z
).
2
k
2
三、正、余弦函数的性质
1.
定义域
:
都是
R.
2.
值域
:
都是
[
-
1, 1].
对
y
=sin
x
,
当
x
=2
k
+
(
k
Z
)
时
,
y
取最大值
1;
当
x
=2
k
+
(
k
Z
)
时
,
y
取最小值
-
1;
对
y
=cos
x
,
当
x
=2
k
(
k
Z)
时
,
y
取最大值
1,
当
x
=2
k
+
(
k
Z)
时
,
y
取最小值
-
1.
2
2
3
3.
周期性
: ①
y
=sin
x
、
y
=cos
x
的最小正周期都是
2
; ②
f
(
x
)=
A
sin(
x
+
)
和
f
(
x
)=
A
cos(
x
+
)
的最小正周期都是
T
= .
|
|
2
4.
奇偶性与对称性
:
正弦函数
y
=sin
x
(
x
R
)
是奇函数
,
对称中心是
(
k
, 0)
(
k
Z
),
对称轴是直线
x
=
k
+
(
k
Z
)
;
余弦函数
y
=cos
x
(
x
R
)
是偶函数
,
对称中心是
(
k
+
, 0)
(
k
Z
),
对称轴是直线
x
=
k
(
k
Z
)
(
正
(
余
)
弦型函数的对称轴为过最高点或最低点且垂直于
x
轴的直线
,
对称中心为图象与
x
轴的交点
)
.
2
2
5.
单调性
:
y
=sin
x
在
[2
k
-
,
2
k
+
]
(
k
Z
)
上单调递增
,
在
[2
k
+
,
2
k
+
]
(
k
Z
)
上单调递减
;
y
=cos
x
在
[2
k
,
2
k
+
]
(
k
Z
)
上单调递减
,
在
[2
k
+
,
2
k
+2
]
(
k
Z
)
上单调递增
.
2
2
2
2
3
2.
值域
是
R,
在上面定义域上无最大值也无最小值
.
1.
定义域
: {
x
|
x
+
k
,
k
Z
}.
2
3.
周期性
:
是周期函数且周期是
,
它与直线
y
=
a
的两个相邻交点之间的距离是一个周期
.
注
一般说来
,
某一周期函数解析式加绝对值或平方
,
其周期性是
:
弦减半、切不变
.
四、正切函数的性质
o
x
y
五、典型例题
例
1
利用单位圆中的三角函数线证明当
0<
<
时
,
不等式
sin
<
cos
x
.
{
x
| +2
k
<
x
< +2
k
,
k
Z
}
4
7
4
3.
求函数
y
=sin
4
x
+2
3
sin
x
cos
x
-
cos
4
x
的最小正周期和最小值
,
并写出该函数在
[0,
]
上的单调增区间
.
解
:
∵
y
=sin
4
x
+2
3
sin
x
cos
x
-
cos
4
x
=(sin
2
x
-
cos
2
x
)
(sin
2
x
+cos
2
x
)+
3
sin2
x
=
3
sin2
x
-
cos2
x
6
=2
sin(2
x
-
)
故该函数的最小正周期是
,
最小值是
-
2.
3
在
[0,
]
上的单调增区间是
[0, ]
和
[ ,
].
6
5
由
2
k
-
≤
2
x
-
≤
2
k
+
(
k
Z
)
得
:
2
2
6
k
-
≤
x
≤
k
+ (
k
Z
).
3
6
令
k
=0,
1
即得函数
y
=sin
4
x
+2
3
sin
x
cos
x
-
cos
4
x
4.
已知函数
y
=
cos
2
x
+
sin
x
cos
x
+1,
x
R
.
(1)
求当
y
取得最大值时自变量
x
的集合
; (2)
该函数的图象可由
y
=sin
x
(
x
R
)
的图象经过怎样的平移和伸缩变换得到
?
1
2
3
2
解
:
(1)
y
=
cos
2
x
+
sin
x
cos
x
+1
=
cos2
x
+
sin2
x
+
1
2
3
2
1
4
3
4
5
4
6
=
sin(2
x
+ )+ .
5
4
1
2
当且仅当
2
x
+ =2
k
+ (
k
Z
),
即
x
=
k
+ (
k
Z
)
时
,
6
2
6
函数
y
取得最大值
.
故当
y
取得最大值时
,
自变量
x
的集合是
:
{
x
|
x
=
k
+
,
k
Z
}.
6
(2)
将函数
y
=
sin
x
依次进行如下变换
:
①
将
y
=
sin
x
的图象向左平移
,
得
y
=
sin(
x
+
)
的图象
;
6
6
②
将所得图象上各点横坐标缩短到原来的 倍
(
纵坐标不变
)
,
得到
y
=
sin(2
x
+
)
的图象
;
1
2
6
③
将所得图象上各点纵坐标缩短到原来的 倍
(
横坐标不变
)
,
得到
y
=
sin(2
x
+
)
的图象
;
1
2
6
1
2
5
4
④
将所得图象向上平移 个单位长度
,
得到
y
=
sin(2
x
+
)
+
的图象
;
1
2
6
5
4
综上得到
y
=
co
s
2
x
+
sin
x
cos
x
+1
的图象
.
3
2
1
2
5.
已知函数
f
(
x
)=sin(
x
+
)(
>0, 0
≤
≤
)
是
R
上的偶函数
,
其图象关于点
M(
, 0)
对称
,
且在区间
[0, ]
上是单调函数
,
求
和
的值
.
4
3
2
解
:
∵
f
(
x
)=sin(
x
+
)(
>0, 0
≤
≤
)
是
R
上的偶函数
,
∴
sin(
-
x
+
)=
sin(
x
+
),
即
-
cos
sin
x
=cos
sin
x
对任
意实数
x
都成立
.
∵
>0,
∴
cos
=0.
又
∵
0
≤
≤
,
∴
= .
2
∵
f
(
x
)
的
图象关于点
M
对称
,
∴
f
(
x
)=cos
x
.
∴
点
M
为
f
(
x
)
图象的一个对称中心
.
∴
=
k
+ (
k
Z
).
4
3
2
∴
= (
k
Z
).
4
k
+2
3
∴
f
(
x
)=cos
x
在区间
[0,
]
上是减函数
.
∵
>0,
2
2
3
综上所述
,
= ,
=2
或
.
2
必有
≤
,
即
0<
≤
2.
∴
要使
f
(
x
)=cos
x
在区间
[0, ]
上是单调函数
,
2
4
k
+2
3
∴
0<
≤
2
(
k
Z).
解得
k
=0
或
1.
2
3
∴
=2
或
.
6.
如果函数
y
=sin2
x
+
a
cos2
x
的图象关于直线
x
=
-
对称
,
求
a
的值
.
8
解
:
y
=sin2
x
+
a
cos2
x
=
a
2
+1
sin(2
x
+
),
其中
, tan
=
a
.
法
1
∵
函数
y
=sin2
x
+
a
cos2
x
的图象关于直线
x
=
-
对称
,
8
∴
当
x
=
-
时
,
y
取最大值或最小值
.
8
∴
2(
-
)+
=
k
+ ,
k
Z
.
2
8
∴
=
k
+
,
k
Z
.
4
3
∴
a
=tan
=tan(
k
+
)=
-
1.
4
3
法
2
∵
函数
y
=sin2
x
+
a
cos2
x
的图象关于直线
x
=
-
对称
,
8
∴
当
x
=
-
时
,
y
取最大值或最小值
.
8
|sin2(
-
)+
a
cos2(
-
)|
2
=
a
2
+1
8
8
解得
a
=
-
1.
法
3
∵
函数
y
=sin2
x
+
a
cos2
x
的图象关于直线
x
=
-
对称
,
8
∴
当自变量取
0,
-
时的函数值相同
.
4
即
0+
a
=
-
1+0.
∴
sin0+
a
cos0=sin2(
-
)+
a
cos2(
-
).
4
4
∴
a
=
-
1.
法
4
∵
函数
y
=sin2
x
+
a
cos2
x
的图象关于直线
x
=
-
对称
,
8
而函数
y
=sin2
x
+
a
cos2
x
的周期为
,
∴
当
x
=
-
+ =
时
,
函数值为
0.
8
4
8
∴
sin +
a
cos
=0.
4
4
∴
a
=
-
1.
课后练习
1.
已知函数
f
(
x
)=log
(sin
x
-
cos
x
), (1)
求它的定义域和值域
; (2)
判断它的单调区间
; (3)
判断它的奇偶性
; (4)
判断它的周期性
,
如果是周期函数
,
求出它的一个周期
.
1
2
解
:
(1)
由
sin
x
-
cos
x
>0,
即
2sin(
x
-
)>0
得
:
4
2
k
+
<
x
<2
k
+
,
k
Z
4
4
5
{
x
|
2
k
+ <
x
<2
k
+
,
k
Z
}.
4
4
5
∴
f
(
x
)
的定义域为
∵
sin
x
-
cos
x
=
2sin(
x
-
)
≤
2
,
4
∴
f
(
x
)=log
(sin
x
-
cos
x
)
≥
log
2 =
-
.
1
2
1
2
1
2
∴
f
(
x
)
的值域为
[
-
, +
∞
).
1
2
(2)
∵
y
=sin
x
-
cos
x
在
f
(
x
)
的定义域上的单调递增区间是
(2
k
+
, 2
k
+
]
(
k
Z
);
4
4
3
[2
k
+
, 2
k
+
)
(
k
Z
),
4
5
4
3
单调递减区间是
[2
k
+
,
2
k
+
)
(
k
Z
).
4
5
4
3
单调递增区间是
(2
k
+
,
2
k
+
]
(
k
Z
);
4
4
3
∴
f
(
x
)
的单调递减区间是
(3)
∵
f
(
x
)
的定义域在数轴上对应的点关于原点不对称
,
∴
函数
f
(
x
)
是非奇非偶函数
.
=log (sin
x
-
cos
x
)
1
2
(4)
∵
f
(
x
+2
)=log [sin(
x
+2
)
-
cos(
x
+2
)]
1
2
=
f
(
x
),
∴
函数
f
(
x
)
是周期函数
,
它的一个周期是
2
.
2.
已知函数
f
(
x
)=Asin(
x
+
)(A
>0,
>0,
x
R
)
在一个周期内的图象如图所示
:
2
3
2
-
2
5
2
7
2
o
x
y
2
求直线
y
= 3
与函数
f
(
x
)
图象的所有交点的坐标
.
2
7
解
:
根据图象得
A=2, T=
-
(
-
)=4
,
2
∴
=
.
1
2
∴
y
=2sin(
x
+
).
1
2
1
2
由
(
-
)+
=0
得
=
.
2
4
∴
y
=2sin(
x
+
).
1
2
4
由
3
=2sin(
x
+
)
得
1
2
4
3
2
sin(
x
+ )=
.
1
2
4
∴
x
+ =2
k
+
或
2
k
+
(
k
Z
).
1
2
4
3
2
3
∴
x
=4
k
+
或
4
k
+
(
k
Z
).
6
5
6
6
6
5
故所有交点坐标为
(4
k
+ ,
3
)
或
(4
k
+
,
3
)
(
k
Z
).
3.
设函数
f
(
x
)=
a
b
,
其中向量
a
=(2cos
x
, 1),
b
=(cos
x
, 3
sin2
x
),
x
R
.
(1)
若
f
(
x
)=1
-
3
且
x
[
-
, ],
求
x
; (2)
若函数
y
=2sin2
x
的图象按向量
c
=(
m
,
n
)(|
m
|<
)
平移后得到函数
y
=
f
(
x
)
的图象
,
求实数
m
,
n
的值
.
3
3
2
解
:
(1)
依题意
f
(
x
)=2cos
2
x
+ 3
sin2
x
=1+2sin(2
x
+
).
6
由
1+2sin(2
x
+
)=
1
-
3
得
:
6
sin(2
x
+
)=
-
.
6
3
2
∵
x
[
-
, ],
∴
2
x
+
[
-
, ].
3
3
2
6
6
5
∴
2
x
+
=
-
.
6
3
∴
x
=
-
.
4
由
(1)
知
f
(
x
)=2sin2(
x
+ )+1.
12
12
∴
m
=
-
,
n
=1.
∵
|
m
|< ,
2
(2)
函数
y
=2sin2
x
的图象按向量
c
=(
m
,
n
)
平移后得到函数
y
=2sin2(
x
-
m
)+
n
即
y
=
f
(
x
)
的图象
.
4.
如图所示
,
某地一天从
6
时到
14
时的温度变化曲线近似满足函数
y
=Asin(
x
+
)+
b
的解析式
,
其中
, A>0,
>0, 0<
<
.
x
y
o
6
10
14
10
20
30
温度
/
℃
时间
/
h
(1)
求这段时间的最大温差
;
(2)
写出这段曲线的函数解析式
.
解
:
(1)
由图示
,
这段时间的最大温差是
:
30
℃-
10℃=20℃.
(2)
图中从
6
时到
14
时的图象是函数
y
=Asin(
x
+
)+
b
半个周期的图象
.
1
2
∴
=14
-
6.
2
解得
= .
8
1
2
又由图示
A=
(30
-
10)=10,
b
=
(30+10)=20,
1
2
8
∴
y
=10sin(
x
+
)+20.
将
x
=6,
y
=10
代入可取
= .
4
3
故所求的解析式为
:
y
=10sin(
x
+ )+20,
x
[6, 14].
8
4
3
5.
已知函数
f
(
x
)=
,
求
f
(
x
)
的定义域
,
判断它的奇偶性
,
并求其值域
.
6cos
4
x
+5sin
2
x
-
4
cos2
x
解
:
由
cos2
x
0
得
2
2
x
k
+
(
k
Z
).
解得
x
+ (
k
Z
).
2
k
4
故
f
(
x
)
的定义域为
{
x
R
|
x
+ ,
k
Z
}.
2
k
4
∵
f
(
x
)
的定义域关于原点对称
,
且
f
(
-
x
)=
6cos
4
(
-
x
)+5sin
2
(
-
x
)
-
4
cos2(
-
x
)
6cos
4
x
-
5cos
2
x
+1
cos2
x
f
(
x
)=
6cos
4
x
+5sin
2
x
-
4
cos2
x
= =
f
(x
),
∴
f
(
x
)
是偶函数
.
当
x
+ (
k
Z
)
时
,
2
k
4
(2cos
2
x
-
1)(3cos
2
x
-
1)
cos2
x
=
=
3cos
2
x
-
1
.
=
+
cos2
x
.
1
2
3
2
1
2
1
2
故
f
(
x
)
的值域为
[
-
1, )
∪
(
, 2].
1
2
6.
已知
f
(
x
)=
-
2
a
sin(2
x
+
)+2
a
+
b
,
x
[ , ],
是否存在常数
a
,
b
Q
,
使得
f
(
x
)
的值域为
[
-
3, 3
-
1]?
若存在
,
求对应的
a
和
b
,
若不存在
,
说明理由
.
6
4
3
4
4
3
解
:
由已知
≤
x
≤
,
4
∴
≤
2
x
+
≤
.
3
2
3
5
6
3
2
∴
-
1
≤
sin(2
x
+
)
≤
.
6
若存在这样的常数
a
,
b
,
则
当
a
>0
时
,
有
-
3
a
+2
a
+
b
=
-
3,
且
4
a
+
b
=
3
-
1.
解得
a
=1,
b
= 3
-
5.
故此时不存在符合条件的
a
,
b
.
∵
b
Q
,
当
a
<0
时
,
有
-
3
a
+2
a
+
b
=
3
-
1,
且
4
a
+
b
=
-
3.
解得
a
=
-
1,
b
=1,
且
a
Q
,
b
Q
.
故符合条件的有理数
a
,
b
存在
,
且
a
=
-
1,
b
=1.