人教A数学必修二 空间几何体的结构导学案

人教A数学必修二 空间几何体的结构导学案

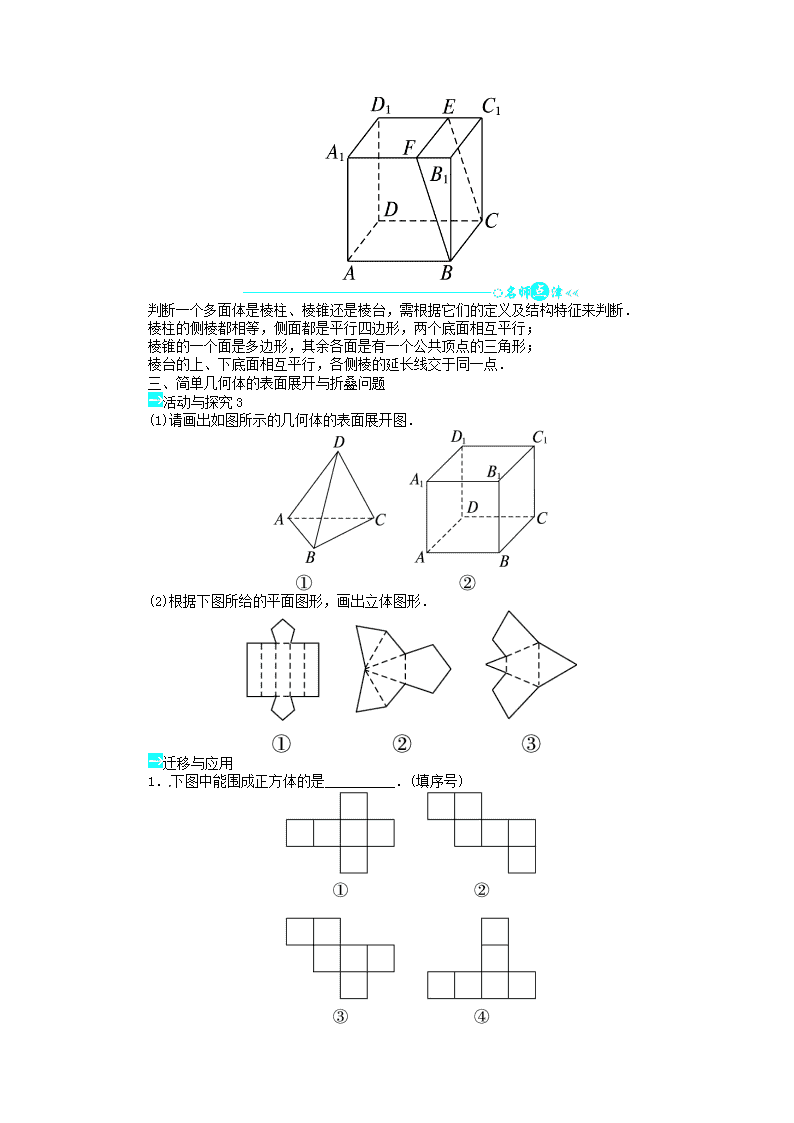
‎1.1　空间几何体的结构 第1课时　棱柱、棱锥、棱台的结构特征 问题导学 一、棱柱、棱锥、棱台的概念 活动与探究1‎ 有下列命题：‎ ‎①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；‎ ‎②各个面都是三角形的几何体是三棱锥；‎ ‎③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫做棱台；‎ ‎④棱柱的各相邻侧面的公共边互相平行．‎ 以上命题中，正确命题的序号是__________．‎ 迁移与应用 ‎1．在棱柱中，(　　)‎ A．只有两个面平行 B．所有的棱都相等 C．所有的面都是平行四边形 D．两底面平行，且各侧棱也平行 ‎2．下列说法正确的是(　　)‎ A．三棱柱有三个侧面、三条侧棱和三个顶点 B．四面体有四个面、六条棱和四个顶点 C．六棱锥有七个顶点 D．棱柱的各条侧棱可以不相等 ‎3．棱台不具有的性质是(　　)‎ A．两底面相似　　 B．侧面都是梯形 C．侧棱都平行 D．侧棱延长后都交于一点 根据形成几何体的结构特征的描述，结合棱柱、棱锥、棱台的定义进行判断，注意判断时要充分发挥空间想象能力，必要时可制作几何模型，通过演示进行准确判断．‎ 二、对多面体形状的认识 活动与探究2‎ 如图，在三棱柱ABC－A1B1C1中，E，F分别是A1B1与A1C1的中点，试判断几何体ABC－A1EF是什么几何体，并指出它的底面与侧面．‎ 迁移与应用 如图，四棱柱ABCD－A1B1C1D1被平面BCEF所截得的两部分分别是怎样的几何体？几何体ABCD－A1FED1若是棱柱，指出它的底面和侧面．‎ 判断一个多面体是棱柱、棱锥还是棱台，需根据它们的定义及结构特征来判断．‎ 棱柱的侧棱都相等，侧面都是平行四边形，两个底面相互平行；‎ 棱锥的一个面是多边形，其余各面是有一个公共顶点的三角形；‎ 棱台的上、下底面相互平行，各侧棱的延长线交于同一点．‎ 三、简单几何体的表面展开与折叠问题 活动与探究3‎ ‎(1)请画出如图所示的几何体的表面展开图．‎ ‎(2)根据下图所给的平面图形，画出立体图形．‎ 迁移与应用 ‎1．下图中能围成正方体的是__________．(填序号)‎ ‎2．在正方形ABCD中，E，F分别为AB，BC的中点，现沿DE，DF，EF把△ADE，△CDF，△BEF折起，使A，B，C三点重合，则折成的几何体为______．‎ ‎(1)解答展开与折叠问题，要结合多面体的结构特征发挥空间想象能力和动手能力．‎ ‎(2)若给出多面体画其展开图时，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面．‎ ‎(3)若是给出表面展开图，则可把上述程序逆推．‎ 当堂检测 ‎1．下列几何体中，棱柱有(　　)‎ A．5个 B．4个 C．3个 D．2个 ‎2．有两个面平行的多面体不可能是(　　)‎ A．棱柱 B．棱锥 C．棱台 D．以上都错 ‎3．下面的多面体是棱台的是(　　)‎ A．两底面是相似多边形的多面体 B．侧面是梯形的多面体 C．两底面平行的多面体 D．两底面平行，侧棱延长后交于一点的多面体 ‎4．一个棱台至少有__________个面，面数最少的棱台有__________个顶点，有__________条棱．‎ ‎5．在下面四个平面图形中，哪几个是各侧棱都相等的四面体的展开图？其序号是__________．(把你认为正确的序号都填上)‎ 提示：用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记．‎ 答案：‎ 课前预习导学 ‎【预习导引】‎ ‎1．(1)形状　大小　空间图形 ‎(2)平面多边形　定直线　封闭几何体　多边形　公共边　棱与棱　定直线 预习交流1　提示：多面体最少有4个面、4个顶点和6条棱．‎ ‎2．每相邻两个四边形　互相平行　相邻侧面　顶点　三棱柱　四棱柱　五棱柱　棱柱ABCDEF－A′B′C′D′E′F′　有一个公共顶点　多边形面　有公共顶点的各个三角形面　侧棱　底面　四面体　棱锥S－ABCD　棱台　下底面、上底面　棱台ABCD－A′B′C′D′‎ 预习交流2　(1)提示：根据棱柱的定义，棱柱的各侧棱互相平行，侧面是平行四边形，两个底面是全等的多边形．‎ ‎(2)提示：根据棱锥的定义，棱锥的侧面一定是三角形，且各个三角形有公共顶点．‎ ‎(3)提示：棱台的各侧棱延长后交于一点，各侧面是梯形，两个底面是相似的多边形．‎ 课堂合作探究 ‎【问题导学】‎ 活动与探究1　④　解析：由图甲知，命题①错误；如图乙，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥，命题②错误；由棱台的定义知，命题③错误；由棱柱的特点知，命题④正确．‎ 迁移与应用　1．D　2．B　3．C 活动与探究2　思路分析：利用棱柱、棱锥、棱台的定义及结构特征判断．‎ 解：∵E，F分别是A1B1，A1C1的中点，且A1B1＝AB，A1C1＝AC，B1C1＝BC，∴＝＝＝．‎ ‎∴△A1EF∽△ABC且AA1，BE，CF延长后交于一点．又平面A1B1C1平行于平面ABC，∴几何体A1EF－ABC是三棱台．其中△ABC是下底面，△A1EF是上底面，四边形ABEA1，四边形BCFE，四边形ACFA1是侧面．‎ 迁移与应用　解：所截两部分分别是四棱柱和三棱柱．几何体ABCD－A1FED1是四棱柱，它的底面是四边形ABFA1和四边形DCED1，侧面为ABCD，BCEF，ADD1A1和A1D1EF．‎ 活动与探究3　思路分析：由题意首先弄清几何体的侧面各是什么形状，然后再通过空间想象或动手实践进行展开或折叠．‎ 解：(1)展开图如图所示：‎ ‎②‎ ‎(2)将各平面图形折起后形成的空间图形如图所示：‎ 迁移与应用　1．①②③‎ ‎2．三棱锥 ‎【当堂检测】‎ ‎1．D　2．B　3．D　4．五　六　九 ‎5．①②‎