2018-2019学年内蒙古赤峰二中高二上学期第二次月考数学（文）试题 Word版

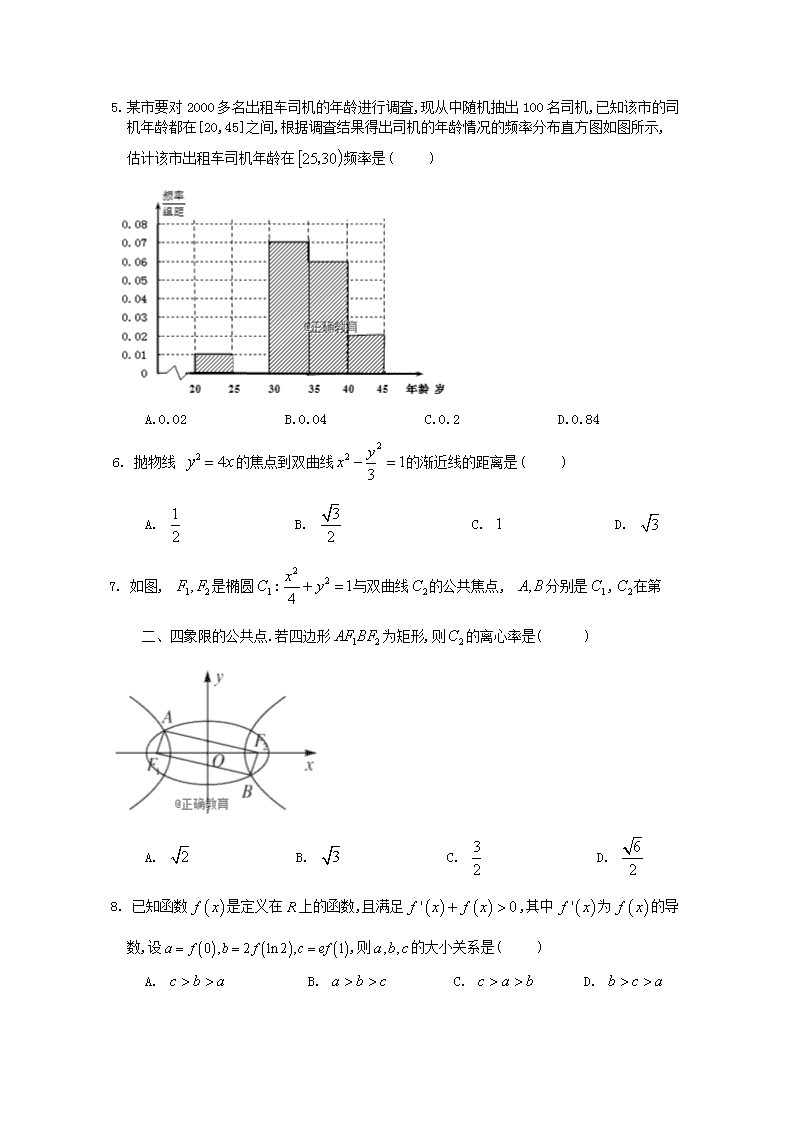
2018-2019学年内蒙古赤峰二中高二上学期第二次月考数学（文）试题 Word版

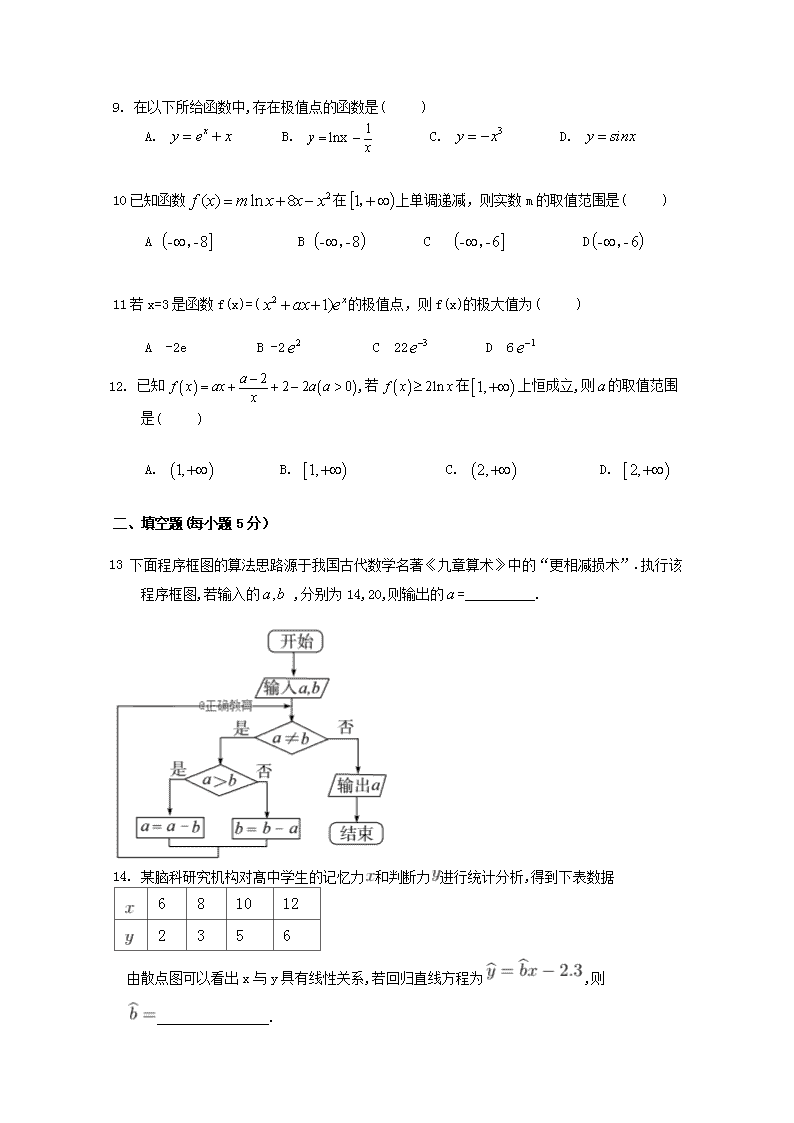
赤峰二中2018-2019学年高二上学期第二次月考 文科数学试题 ‎（2018年12月7日）‎ 一、选择题（每小题5分)‎ ‎1. 某城市有学校700所.其中大学20所,中学200所,小学480所,现用分层抽样方法从抽取一个容量为70的样本,则应抽取中学数为(   )‎ A.70         B.20         C.48         D.2‎ ‎2. 如图给出的是计算的值的一个程序框图,则判断框内可以填入的条件是(   )‎ A. B. C. D. ‎ ‎3. 某班有学生60人,现将所有学生按1,2, 3,…,60随机编号,若采用系统抽样的方法抽取一个容量为4的样本(等距抽样),已知编号为3, 33, 48号学生在样本中,则样本中另一个学生的编号为(   )‎ A.28         B.23         C.18         D.13‎ ‎4. 甲、乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别为、,则下列判断正确的是(   )‎ A.,甲比乙成绩稳定 B.,乙比甲成绩稳定 C.,甲比乙成绩稳定 D.,乙比甲成绩稳定 ‎5. 某市要对2000多名出租车司机的年龄进行调査,现从中随机抽出100名司机,已知该市的司机年龄都在[20,45]之间,根据调査结果得出司机的年龄情况的频率分布直方图如图所示,估计该市出租车司机年龄在频率是(   )‎ A.0.02       B.0.04       C.0.2       D.0.84‎ ‎6. 抛物线 的焦点到双曲线的渐近线的距离是(   )‎ A. B. C. D. ‎ ‎7. 如图, 是椭圆:与双曲线的公共焦点, 分别是,在第 二、四象限的公共点.若四边形为矩形,则的离心率是(   )‎ A. B. C. D. ‎ ‎8. 已知函数是定义在上的函数,且满足,其中为的导数,设,则的大小关系是(   )‎ A. B. C. D. ‎ ‎9. 在以下所给函数中,存在极值点的函数是(   )‎ A. B. C. D. ‎ ‎10已知函数在上单调递减，则实数m的取值范围是(   )‎ A B C D ‎11若x=3是函数f(x)=(的极值点，则f(x)的极大值为(   )‎ A -2e B -2 C 22 D 6‎ ‎12. 已知,若在上恒成立,则的取值范围是(   )‎ A. B. C. D. ‎ 二、填空题(每小题5分）‎ ‎13 下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的 ,分别为14,20,则输出的=__________.‎ ‎14. 某脑科研究机构对髙中学生的记忆力和判断力进行统计分析,得到下表数据 ‎ ‎6 ‎ ‎8 ‎ ‎10 ‎ ‎12 ‎ ‎2 ‎ ‎3 ‎ ‎5 ‎ ‎6 ‎ 由散点图可以看出x与y具有线性关系,若回归直线方程为,则        . ‎ ‎15 函数y=有三个相异的零点，则的取值范围为        ‎ ‎16 已知直线 与曲线相切,其中为自然对数的底数,则实数的值为        ‎ 三 解答题 ‎17（10分） 设函数过点 ‎1.求函数的单调区间和极大值;‎ ‎2.求函数在上的最小值 ‎18（12分） 从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表: ‎ 质量指标值分组 ‎ ‎[75,85) ‎ ‎[85,95) ‎ ‎[95,105) ‎ ‎[105,115) ‎ ‎[115,125) ‎ 频数 ‎ ‎6 ‎ ‎26 ‎ ‎38 ‎ ‎22 ‎ ‎8 ‎ ‎1.在表格中作出这些数据的频率分布直方图;‎ ‎2求这些数据的众数和中位数 ‎3.估计这种产品质量指标的平均数(同一组中的数据用该组区间的中点值作代表);‎ ‎ ‎ ‎19（12分） 已知函数.‎ ‎1.若,求函数在处的切线方程;‎ ‎2.若 的导数为，g(x)=,求g(x)的单调区间 ‎20（12分） 我校的课外综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到市气象观测站与市医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:‎ 日期 ‎1月10日 ‎2月10日 ‎3月10日 ‎4月10日 ‎5月10日 ‎6月10日 昼夜温差 ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ ‎6‎ ‎22‎ ‎25‎ ‎29‎ ‎26‎ ‎16‎ ‎12‎ 该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验 ‎1.若选取的是月与月的两组数据,请根据至月份的数据,求出关于的线性回归方程 ‎2.若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?参考数据: ,‎ 参考公式:回归直线,其中 ‎21.（12分） 椭圆的短轴两端点为、,离心率,点是椭圆上不在坐标轴上的任意一点,直线和分别与轴相交于两点 ‎1.求椭圆的方程和的值;‎ ‎2.若点坐标为,过点的直线与椭圆相交于两点,试求面积的最大值.‎ ‎22.（12分） 设函数 若对任意恒成立,求实数的取值范围.‎ 高二文科第二次月考数学答案 一BBCBC BDADA DB 二2； 0.7； （-2,2）；1‎ 三17答案：1. 点在函数的图象上,∴,解得,‎ ‎∴当或时 单调递增;当时, ,单调递减.‎ 当时, 有极大值,且极大值为.‎ ‎2.由可得:函数在区间上单调递减,在区间上单调递增 ‎18答案：‎ ‎2.众数100 中位数95.47 3. =100‎ ‎19答案：1.∵∵ ∴切线方程为即 ‎2 a≤0,增区间，a>0,增区间，减区间 ‎20答案：1.∵,‎ ‎,‎ ‎,‎ 故关于的回归直线方程: 2.当时, ;‎ 而当时, ,.‎ ‎∴该小组所得线性回归方程是理想的 ‎21答案：1.由 、,知,‎ 又,所以,‎ 则,所以椭圆的方程为,  ‎ 设点,则直线方程为,‎ 令得,‎ 同理可得,. 2.当点 坐标为时,点,,‎ 设直线的方程为,,,‎ 代入方程得,则 ‎,‎ ‎,‎ 因为,所以, ‎ 因此当,即直线的方程为时,‎ 面积的最大值是.‎ ‎22答案：1.当时, ,,所以曲线在点处的切线方程为即. 2.设则当时, 在上单调递增,所以,对任意,有,所以当时, 在上单调递减,在上单调递增,所以,由条件知, ,即设则所以在上单调递减,又,所以与条件矛盾.综上可知,实数的取值范围为