数学理（B）卷·2018届广东省清远市清城区高二上学期期末考试（2017-01）

数学理（B）卷·2018届广东省清远市清城区高二上学期期末考试（2017-01）

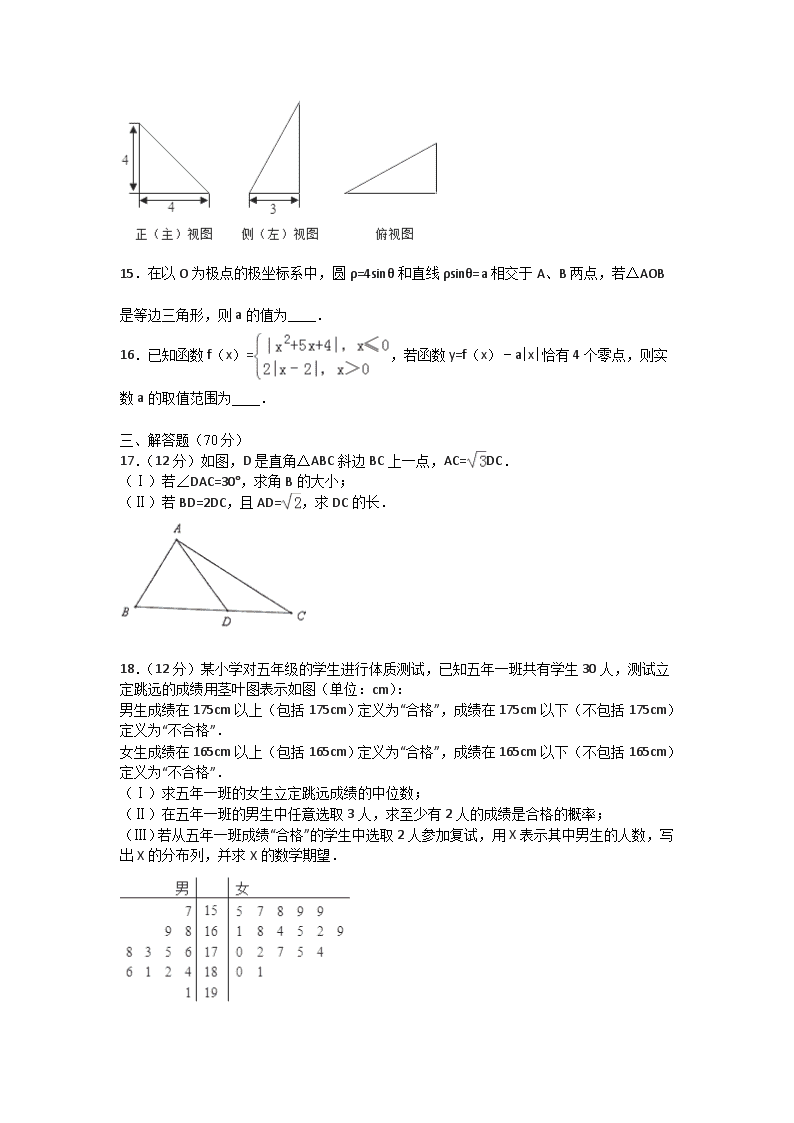
广东省清远市清城区高二第一学期期末统考（B）卷 数学（理）试题 ‎(本卷满分150分，时间120分钟)‎ 一、 选择题（60分，每题5分）‎ ‎1．已知全集U=R，A={x|x2+2x≤0}，B={x|x＞﹣1}，则集合∁U（A∩B）=（　　）‎ A．（﹣∞，﹣1]∪（0，+∞） B．（﹣∞，﹣1）∪0，+∞） C．（﹣1，0] D．﹣1，0）‎ ‎2．复数z=（sinθ﹣2cosθ）+（sinθ+2cosθ）i是纯虚数，则sinθcosθ=（　　）‎ A．﹣ B．﹣ C． D．‎ ‎3．已知函数f（x）为定义在R上的奇函数，则下列函数中为奇函数的是（　　）‎ ‎①y=f（|x|）‎ ‎②y=f（﹣x） ‎ ‎③y=xf（x） ‎ ‎④y=f（x）﹣x．‎ A．①③ B．②③ C．①④ D．②④‎ ‎4．（5分）等比数列{an}中，a3=5，a8=2，则数列{lgan}的前10项和等于（　　）‎ A．2 B．5 C．10 D．lg50‎ ‎5．阅读如图的程序框图，运行相应的程序，则输出的S的值为（　　）‎ A．2 B．4 C．8 D．16‎ ‎6．设等差数列{an}的前n项和为Sn，若Sk﹣1=﹣3，Sk=0，Sk+1=4，则k=（　　）‎ A．5 B．6 C．7 D．8‎ ‎7．在△ABC中，∠ABC=90°，AB=，BC=2，点P为△ABC内一点，若∠BPC=90°，PB=1，则PA=（　　）‎ A．4﹣ B． C． D．1‎ ‎8．已知菱形ABCD的边长为2，∠BAD=120°，点E、F分别在边BC、DC上，=λ，=μ，若•=1，•=﹣，则λ+μ=（　　）‎ A． B． C． D．‎ ‎　‎ ‎9．若不等式组表示的区域Ω，不等式（x﹣）2+y2表示的区域为Γ，向Ω区域均匀随机撒360颗芝麻，则落在区域Γ中芝麻数约为（　　）‎ A．114 B．10 C．150 D．50‎ ‎10．已知抛物线y2=2px（p＞0）的焦点F恰好是双曲线﹣=1（a＞0，b＞0）的一个焦点，两条曲线的交点的连线过点F，则双曲线的离心率为（　　）‎ A． B． C．1+ D．1+‎ ‎11．在四面体S﹣ABC中，SA⊥平面ABC，∠BAC=120°，SA=AC=2，AB=1，则该四面体的外接球的表面积为（　　）‎ A．11π B．7π C． D．‎ ‎12．已知函数f（x）=，若关于x的方程f2（x）﹣bf（x）+c=0（b，c∈R）有8个不同的实数根，则由点（b，c）确定的平面区域的面积为（　　）‎ A． B． C． D．‎ 一、 填空题（20分，每题5分）‎ ‎13．如图，向边长为1的正方形内随机的投点，所投的点落在由y=x2和y=x围成的封闭图形的概率为　　．‎ ‎14．某四面体的三视图如图所示，该四面体四个面的面积中最大的是　　．‎ 15． 在以O为极点的极坐标系中，圆ρ=4sinθ和直线ρsinθ=a相交于A、B两点，若△AOB 是等边三角形，则a的值为　　．‎ ‎16．已知函数f（x）=，若函数y=f（x）﹣a|x|恰有4个零点，则实数a的取值范围为　　．‎ 一、 解答题（70分）‎ ‎17．（12分）如图，D是直角△ABC斜边BC上一点，AC=DC．‎ ‎（Ⅰ）若∠DAC=30°，求角B的大小；‎ ‎（Ⅱ）若BD=2DC，且AD=，求DC的长．‎ ‎18．（12分）某小学对五年级的学生进行体质测试，已知五年一班共有学生30人，测试立定跳远的成绩用茎叶图表示如图（单位：cm）：‎ 男生成绩在175cm以上（包括175cm）定义为“合格”，成绩在175cm以下（不包括175cm）定义为“不合格”．‎ 女生成绩在165cm以上（包括165cm）定义为“合格”，成绩在165cm以下（不包括165cm）定义为“不合格”．‎ ‎（Ⅰ）求五年一班的女生立定跳远成绩的中位数；‎ ‎（Ⅱ）在五年一班的男生中任意选取3人，求至少有2人的成绩是合格的概率；‎ ‎（Ⅲ）若从五年一班成绩“合格”的学生中选取2人参加复试，用X表示其中男生的人数，写出X的分布列，并求X的数学期望．‎ ‎19．（12分）设函数f（x）=cos2x+sin2（x+）．‎ ‎（Ⅰ）求f（x）的最小正周期和单调递增区间；‎ ‎（Ⅱ）当x∈﹣，）时，求f（x）的取值范围．‎ ‎20．（12分）已知单调递增的等比数列{an}满足a2+a3+a4=28，且a3+2是a2，a4的等差中项．‎ ‎（I）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=an•log2an，其前n项和为Sn，若（n﹣1）2≤m（Sn﹣n﹣1）对于n≥2恒成立，求实数m的取值范围．‎ ‎21、（12分）已知椭圆C：+=1（a＞b＞0）的离心率为，以原点为圆心，椭圆的短半轴为半径的圆与直线x﹣y+=0相切，过点P（4，0）且不垂直于x轴直线l与椭圆C相交于A、B两点．‎ ‎（1）求椭圆C的方程；‎ （2） 求•的取值范围；‎ （3） 若B点关于x轴的对称点是E，证明：直线AE与x轴相交于定点．‎ ‎22、（10分）已知曲线C的极坐标方程为2ρsinθ+ρcosθ=10．曲线 c1：（α为参数）．‎ ‎（Ⅰ）求曲线c1的普通方程；‎ ‎（Ⅱ）若点M在曲线C1上运动，试求出M到曲线C的距离的最小值．‎ 数学（理）答案 ‎ 一、ACDB CCCC ACDA 二、13、 14、10 15、3 16、（1，2）‎ 三、‎ ‎17、解：（Ⅰ）在△ABC中，根据正弦定理，有=．‎ ‎∵AC=DC，∴sin∠ADC==．‎ 又∠ADC=∠B+∠BAD=∠B+60°＞60°，‎ ‎∴∠ADC=120°．‎ 于是∠C=180°﹣120°﹣30°=30°，∴∠B=60°．‎ ‎（Ⅱ）设DC=x，则BD=2x，BC=3x，AC=x．‎ 于是sinB==，cosB=，AB=x．‎ 在△ABD中，由余弦定理，AD2=AB2+BD2﹣2AB•BDcosB，‎ 即，得x=1．故DC=1．‎ ‎18、解：（I）由茎叶图得五年一班的女生立定跳远成绩的中位数为cm．…（2分）‎ ‎（II）设“仅有两人的成绩合格”为事件A，“有三人的成绩合格”为事件B，‎ 至少有两人的成绩是合格的概率：P=P（A）+P（B），‎ 又男生共12人，其中有8人合格，从而，‎ ‎，所以．‎ ‎（III）因为女生共有18人，其中有10人合格，‎ 依题意，X的取值为0，1，2．‎ 则，‎ ‎，‎ ‎，‎ ‎（每项1分）（10分）‎ 因此，X的分布列如下：‎ X ‎0‎ ‎1‎ ‎2‎ P ‎∴（人）．（未化简不扣分）‎ ‎（或是，因为X服从超几何分布，所以（人）．‎ ‎19、解：f（x）=cos2x+sin2（x+）．‎ ‎⇔f（x）=cos2x+‎ ‎⇔f（x）=cos2x+sin2x+‎ ‎⇔f（x）=sin（2x+）+，‎ ‎（1）最小正周期，‎ ‎∵sinx单调递增区间为2kπ﹣，2kπ+]，（k∈Z）‎ ‎∴2x∈2kπ﹣，2kπ+]，（k∈Z）‎ 解得：x∈，]，（k∈Z）‎ ‎∴f（x）的最小正周期为π；单调递增区间为，]，（k∈Z）‎ ‎（2）由（1）得：f（x）=sin（2x+）+‎ ‎∵x∈﹣，），‎ ‎∴2x∈，]，‎ 由三角函数的图象和性质：‎ 可知：当2x=时，f（x）取得最小值，即=0．‎ 当2x=时，f（x）取得最大值，即．‎ ‎∴x∈﹣，）时，f（x）的取值范围在．‎ ‎20、解：（Ⅰ）设等比数列的{an}首项为a1，公比为q．‎ 由题意可知：，‎ 解得：或，‎ ‎∵数列为单调递增的等比数列，‎ ‎∴an=2n；‎ ‎（Ⅱ）bn=an•log2an =n•2n，‎ ‎∴Sn=b1+b2+…+bn=1•21+2•22+…+n•2n，①‎ ‎2Sn=1•22+2•23+3•24+…+n•2n+1，②‎ ‎①﹣②，得：﹣Sn=2+22+23+…+2n﹣n•2n+1‎ ‎=﹣n•2n+1=2n+1﹣2﹣n•2n+1，‎ ‎∴Sn=（n﹣1）•2n+1+2，‎ 若（n﹣1）2≤m（Sn﹣n﹣1）对于n≥2恒成立，‎ 则（n﹣1）2≤m（n﹣1）•2n+1+2﹣n﹣1]=m（n﹣1）•2n+1+1﹣n]对于n≥2恒成立，‎ 即=对于n≥2恒成立，‎ ‎∵=，‎ ‎∴数列{}为递减数列，‎ 则当n=2时，的最大值为．‎ ‎∴m≥．‎ 则实数m得取值范围为，+∞）．‎ ‎21、（1）解：由题意知，，即b=‎ 又a2=b2+c2‎ ‎∴a=2，b=‎ 故椭圆的方程为（2分）‎ ‎（2）解：由题意知直线l的斜率存在，设直线l的方程为y=k（x﹣4）‎ 由可得：（3+4k2）x2﹣32k2x+64k2﹣12=0（4分）‎ 设A（x1，y1），B （x2，y2），则△=322k4﹣4（3+4k2）（64k2﹣12）＞0‎ ‎∴（6分）‎ ‎∴x1+x2=，x1x2=①‎ ‎∴=x1x2+y1y2=‎ ‎=‎ ‎=‎ ‎=‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴）‎ ‎（3）证明：∵B，E关于x轴对称 ‎∴可设E（x2，﹣y2）‎ ‎∴直线AE的方程为 令y=0可得x=‎ ‎∵y1=k（x1﹣4），y2=k（x2﹣4）‎ ‎∴==1‎ ‎∴直线AE与x轴交于定点（1，0）‎ ‎22、解：（Ⅰ）∵，∴cosα=，sinα=，∴曲线C1的普通方程是：．‎ ‎（Ⅱ）曲线C的普通方程是：x+2y﹣10=0．‎ 点M到曲线C的距离为，（）．‎ ‎∴α﹣φ=0时，，此时．‎