肇庆市2021届高中毕业班第一次统一检测试题

肇庆市2021届高中毕业班第一次统一检测试题

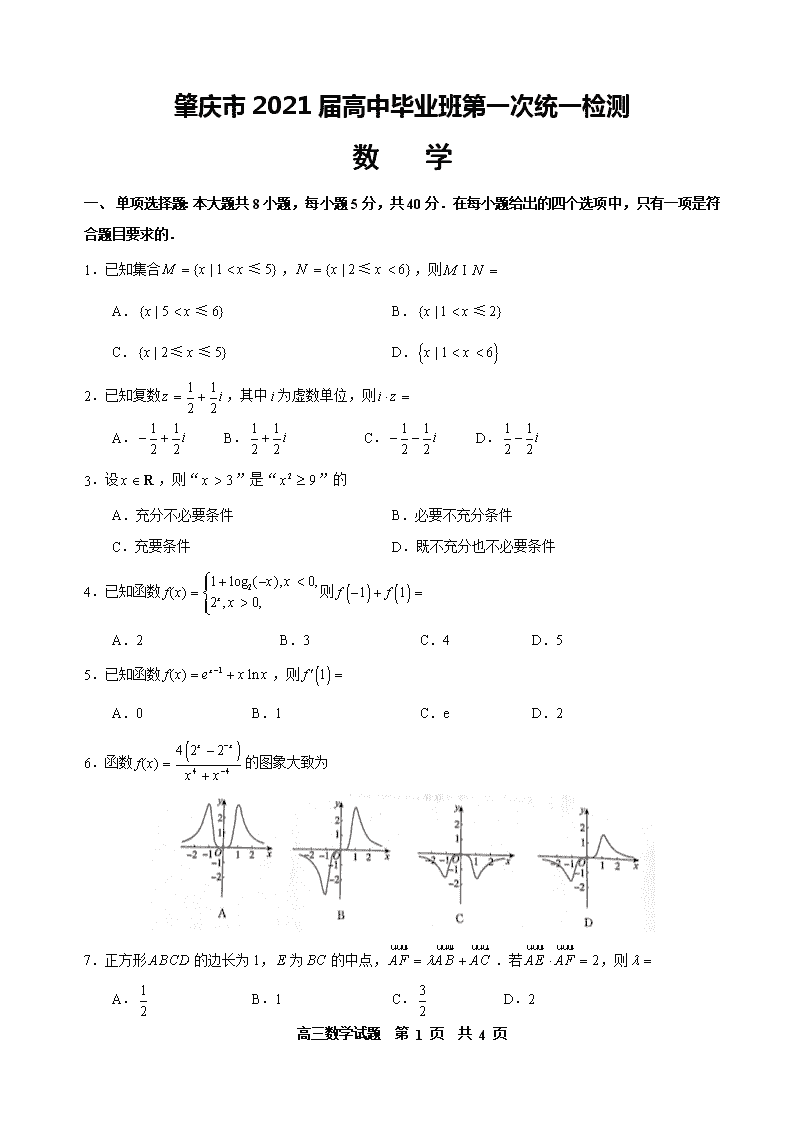
高三数学试题 第 1 页 共 4 页 肇庆市 2021 届高中毕业班第一次统一检测 数 学 一、 单项选择题：本大题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有一项是符 合题目要求的． 1．已知集合 }1{ 5|M x x  ≤ ， }2{ 6|N x x ≤ ，则M N I A．{ | }5 6x x ≤ B．{ | }1 2x x ≤ C．{ | }2 5x x≤ ≤ D． 6|1x x  2．已知复数 1 1 2 2 z i  ，其中i 为虚数单位，则i z  A． 1 1 2 2 i  B． 1 1 2 2 i C． 1 1 2 2 i  D． 1 1 2 2 i 3．设x  R ，则“ 3x  ”是“ 2 9x  ”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 4．已知函数 21 log ( ), 0, ( ) 2 , 0,x x x f x x       则    1 1f f   A．2 B．3 C．4 D．5 5．已知函数 1( ) lnxf x e x x  ，则  1f   A．0 B．1 C．e D．2 6．函数   4 4 4 2 2 ( ) x x f x x x      的图象大致为 7．正方形ABCD 的边长为 1，E 为BC 的中点， AF AB AC  uuur uuur uuur ．若 2AE AF  uuur uuur ，则   A． 1 2 B．1 C． 3 2 D．2 8．某公园有一个边长为2 m 的等边三角形花圃，现要在花圃中修一条篱笆，将花圃分成面积相等的两部 高三数学试题 第 2 页 共 4 页 分，则篱笆的最短长度为 A． 3m B． 3 2 m C．1 m D． 2m 二、多项选择题：本题共 4 小题．每小题 5 分．共 20 分．在每小题给出的四个选项中，有多项是符合题 目要求的．全部选对得 5 分，部分选对得 3 分，有选错的得 0 分． 9．设 ,a b 是两条不重合的直线， ,  是两个不同的平面．下列四个命题中，正确的是 A．若a P ，b P ，则a bP B．若a  ，b  ，则a bP C．若a  ，a  ，则 P D．若a  ，b P ，则a b 10．等差数列 na 中， 5 11a  , 12 10a   ， nS 是数列 na 的前n 项和，则 A． 1 16 1a a  B． 8S 是 nS 中的最大项 C． 9S 是 nS 中的最小项 D． 8 9a a 11．如图是函数    sin 0,| | 2 f x x            的部分图象， 下 列选项正确的是 A． ( ) sin(2 ) 3 f x x   B． ( ) sin(4 ) 3 f x x   C． ( ) 0 6 f   D． 2( ) 1 3 f   12．下列大小关系正确的有 A． 2.1 22 2.1 B． 3.9 22 3.9 C． 1 ln2 ln2 2  D． 5 8log 3 log 5 三、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．已知 1sin 3 x  ，则 cosx  ▲ ． 14．已知  f x 是定义在 R 上的奇函数，且    4f x f x  ．若  2 2f  ，则  6f  ▲ ． 15．已知等比数列 na 中， 2 1S  ， 2 3 2a a  ，则 6S  ▲ ． 16．鳖臑（biē nào）出自《九章算术·商功》：“斜解立方，得两壍堵．斜 解壍堵， 其一为阳马，一为鳖臑。”鳖臑是我国对四个面均为直角三角形的三棱锥 的 古 称．如图，三棱锥 A BCD 是一个鳖臑，其中 AB BC ， AB BD ， BC CD ，且 4AB BC DC   ，过点B 向AC 引垂线，垂足为E ，过 E 作 CD 的平行线，交AD 于点F ，连接BF ．设三棱锥A BCD 的外接球的表面积为 1S ，三棱锥A BEF 的 高三数学试题 第 3 页 共 4 页 外接球的表面积为 2S ，则 1 2 S S  ▲ ． 四、解答题：本题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分 10 分） 在① 3 3 2ABCS  ，② sin 3 sinA C ，③ 2sin 2 C  这三个条件中任选一个，补充在下面的问题 中．若问题中的三角形存在，求出a 的值；若问题中的三角形不存在，说明理由． 问题：是否存在 ABC ，它的内角A ，B ，C 所对的边分别为a ，b ，c ，且 3b  ，sin 3 cos 0A A  ， ▲ ？ 注：如果选择多个条件分别解答，按第一个解答计分． 18．（本小题满分 12 分） 已知函数   3 21 ( 1) 3 f x x ax a x    ． （1）当 1a  时，求  f x 在   1, 1f 处的切线方程； （2）设  f x 是函数  f x 的导函数，求  f x 零点之间距离最小时a 的值． 19．（本小题满分 12 分） 如图，棱长为 2 的正四面体ABCD （所有棱长均相等的三棱锥）中，E ，F 为AB 和DC 的中点． （1）证明：AB CD ； （2）求三棱锥D EFB 的体积． 20．（本小题满分 12 分） 已知函数   223 sin( 2 ) 4 cos 3 3 f x x x    ． （1）求函数  f x 的最小正周期； （2）求函数  f x 在区间 2, 12 3       上的值域． 21．（本小题满分 12 分） 已知数列 na 的前n 项和为 nS ，  *1 1 2n na S n   N ． 高三数学试题 第 4 页 共 4 页 （1）求 nS ； （2）若 2 1log 2n n n nb a a       ，求数列 nb 的前n 项和 nT ． 22．（本小题满分 12 分） 已知函数   1ln 2 f x x ax   ． （1）讨论函数  f x 的单调性； （2）若 1x  是函数    g x xf x 的极值点，求证：函数  g x 存在唯一的极大值点 0x ，且  0 1 0 2 g x   ．（参考数据： ln2 0.693 ）