专题3-3+导数的综合应用（练）-2018年高考数学（文）一轮复习讲练测

专题3-3+导数的综合应用（练）-2018年高考数学（文）一轮复习讲练测

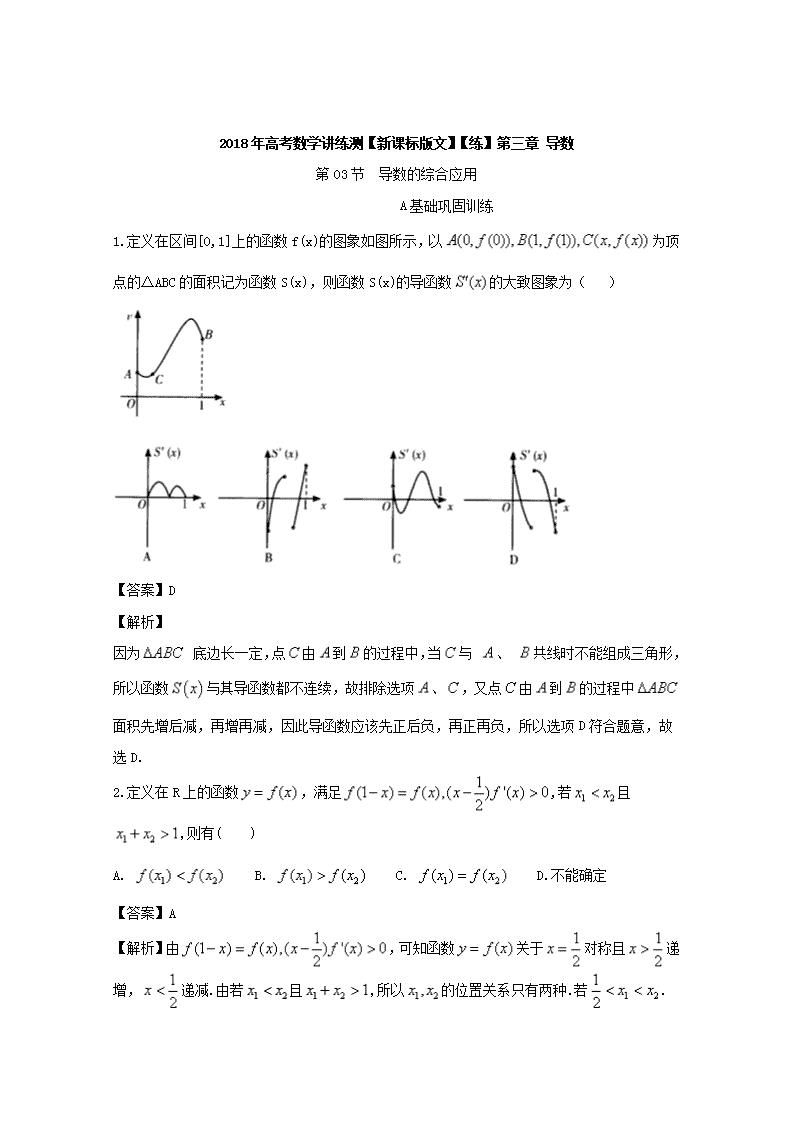
‎2018年高考数学讲练测【新课标版文】【练】第三章 导数 第03节 导数的综合应用 A基础巩固训练 ‎1.定义在区间[0,1]上的函数f(x)的图象如图所示，以为顶点的△ABC的面积记为函数S(x)，则函数S(x)的导函数的大致图象为（ ）‎ ‎【答案】D ‎【解析】‎ 因为 底边长一定，点由到的过程中，当与 、 共线时不能组成三角形，所以函数与其导函数都不连续，故排除选项、，又点由到的过程中面积先增后减，再增再减，因此导函数应该先正后负，再正再负，所以选项D符合题意，故选D.‎ ‎2.定义在R上的函数，满足,若且,则有( )‎ A. B. C. D.不能确定 ‎【答案】A ‎【解析】由，可知函数关于对称且递增，递减.由若且,所以的位置关系只有两种.若 ‎.则成立.若.则.根据对称性可得.综上结论成立.‎ ‎3.【2017河北武邑三调】已知是定义在上的偶函数，其导函数为,若 ，且，则不等式的解集为（ ）‎ A． B． C. D．‎ ‎【答案】A ‎【解析】可取特殊函数，故选A.‎ ‎4．己知定义在上的可导函数的导函数为，满足，且为偶函数，，则不等式的解集为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎5.【2017山西大学附中二模】设函数，其中，若存在唯一的整数，使得，则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】令.由题意知存在唯一整数，使得在直线 的下方.，当时，函数单调递减，当，函数单调递增，当时，函数取得最小值为.当时，，当时，，直线过定点，斜率为，故且，解得.‎ B能力提升训练 ‎1．【四川成都树德中学高三模拟】若方程在上有解，则实数的取值范围是（ ）‎ A． B． C． D．∪‎ ‎【答案】A ‎2．【2017四川泸州四诊】已知函数，关于的不等式只有两个整数解，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】函数f(x)的定义域为(0,+∞)，则，当f′(x)>0得1−ln(2x)>0,即ln(2x)<1，即0<2x1，即2x>e,即，即当时,函数f(x)取得极大值,同时也是最大值，即当 时, 有一个整数解1，‎ 当时, 有无数个整数解，若a=0,则f2(x)+af(x)>0得f2(x)>0，此时有无数个整数解，不满足条件。若a>0，则由f2(x)+af(x)>0得f(x)>0或f(x)<−a，当f(x)>0时，不等式有无数个整数解，不满足条件。‎ 当a<0时,由f2(x)+af(x)>0得f(x)>−a或f(x)<0，当f(x)<0时，没有整数解，则要使当f(x)>−a有两个整数解，‎ ‎∵，‎ ‎∴当f(x)⩾ln2时,函数有两个整数点1,2,当时，函数有3个整数点1，2，3，‎ ‎∴要使f(x)>−a有两个整数解，则，即，本题选择A选项.‎ ‎3．【2017广东惠州二调】已知定义在上的函数满足：函数的图象关于直线对称，且当成立(是函数的导函数), 若，，, 则的大小关系是（ ） ‎ ‎（A） （B） （C） （D） ‎ ‎【答案】A ‎【解析】∵函数的图象关于直线对称，∴关于轴对称， ∴函数为奇函数. 因为，‎ ‎ ∴当时，，函数单调递减，‎ ‎ 当时，函数单调递减.‎ ‎，， ，，故选A.‎ ‎4.已知函数是偶函数，是它的导函数，当时，恒成立，且，则不等式的解集为 .‎ ‎【答案】‎ ‎【解析】令则函数是奇函数，当时，，因此在上单调减，从而在上单调增，由得或，解得或所求解集为.‎ ‎5．已知函数，．‎ ‎（Ⅰ）讨论函数的单调性；‎ ‎（Ⅱ）若函数有两个零点，求实数的取值范围．‎ ‎【答案】（Ⅰ）当时，上单调递减；当时，函数在上单调递减，在上单调递增；（Ⅱ）．‎ ‎【解析】‎ ‎（Ⅰ）‎ ‎① 当上单调递减；‎ ‎② 当.‎ ‎.‎ ‎∴函数在上单调递减，在上单调递增 ‎ 综上：当上单调递减；‎ 当时，函数在上单调递减，在上单调递增 ‎（Ⅱ）当由（Ⅰ）得上单调递减，函数不可能有两个零点；‎ 当a>0时，由（Ⅰ）得，且当x趋近于0和正无穷大时，都趋近于正无穷大，‎ 故若要使函数有两个零点，则的极小值，‎ 即，解得,‎ 综上所述，的取值范围是 ‎ ‎ C 思维拓展训练 ‎1.设函数有两个极值点，若点为坐标原点，点在圆上运动时，则函数图象的切线斜率的最大值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 因为 ，所以，又因为点为坐标原点，所以,，，，,又点 在圆 上运动，所以,,表示是圆上动点与原点连线的斜率，由几何意义可求得的最大值为，因此的最大值为，故选D.‎ ‎2．已知函数对于使得成立，则的最小值为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由题意令，则，从而，由得，而当时是单调递增函数，所以当时；当时；因此时取最小值：选B．‎ ‎3.若不等式对任意的，恒成立，则实数的取值范围是 ． ‎ ‎【答案】‎ ‎4．【2017安徽马鞍山二模】已知函数．‎ ‎（Ⅰ）证明曲线上任意一点处的切线斜率不小于2；‎ ‎（Ⅱ）设，若有两个极值点，且，证明： ．‎ ‎【答案】(Ⅰ) 见解析(Ⅱ)见解析 ‎【解析】试题分析：(Ⅰ)先求导函数，只需证明成立即可；（Ⅱ）令， ，可知两根为，结合韦达定理可化简得，研究函数的单调性，可证结论.‎ 当时， ，‎ 由得， ，设两根为，则，‎ 其中，‎ 在上递增，在上递减，在上递增， ‎ 从而有两个极值点，且， ‎ ‎，‎ 即， ‎ 构造函数， ，‎ 所以在上单调递减， 且．故．‎ ‎5．【2017重庆二诊】已知曲线在点处的切线与直线平行， ．‎ ‎（1）求的值；‎ ‎（2）求证： ．‎ ‎【答案】（Ⅰ）；（Ⅱ）见解析.‎ ‎【解析】‎ 试题分析：（１）先求导数，再运用导数的几何意义建立方程求解；（２）先将不等式进行等价转化，再运用导数分别求不等式中的两边的函数的最值进行分析推证：‎ ‎（Ⅰ），由题；‎ ‎（Ⅱ）， ， ，‎ 故在和上递减，在上递增， ‎ ‎①当时， ，而，故在上递增，‎ ‎， 即； ‎ ‎②当时， ，令，则 故 在上递增， 上递减， ， 即；‎ 综上，对任意，均有.‎ ‎ ‎