四川省武胜烈面中学校2019-2020学年高二上学期期中考试数学（文）试题

四川省武胜烈面中学校2019-2020学年高二上学期期中考试数学（文）试题

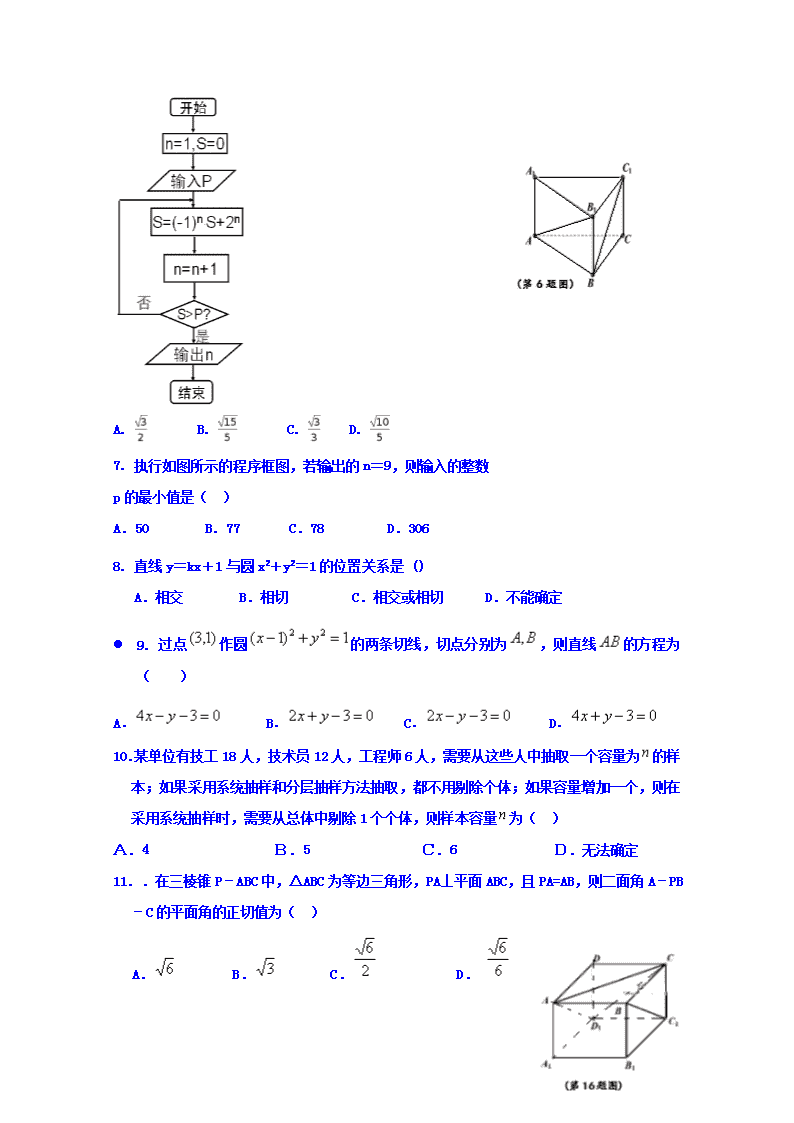
烈面中学高2018级高二上期中期考试试题 文 科 数 学 ‎（考试时间：120分钟 总分：150分） 命题：何红林 一. 选择题（共12小题，60分） 审题：谭 森 ‎1. 如图所示,正方体ABCD－A1B‎1C1D1的棱长为1,则点B1的坐标是( )‎ A.(1,0,0) B.(1,0,1) C.(1,1,1) D.(1,1,0)‎ ‎ ‎ ‎2.如图所示，若直线l1，l2，l3的斜率分别为k1，k2，k3，则( )‎ ‎ (第1题图)‎ A．k1＜k2＜k3 B． k3＜k1＜k‎2 C．k3＜k2＜k1 D．k1＜k3＜k2‎ ‎ ‎ ‎3. 若表示两条直线，表示平面，下列说法中正确的为（ ）‎ A．若，，则 B．若，，则 C．若，，则 D．若，，则 ‎4. 与直线l：3x－5y＋4＝0关于x轴对称的直线的方程为( ) (第2题图)‎ ‎ ‎ A. 3x＋5y＋4＝0 B. 5x－3y＋4＝‎0 C. 3x－5y－4＝0 D.5x＋3y＋4＝0‎ ‎5.若方程表示圆，则的取值范围是( )‎ A. Ｂ. C. D.‎ ‎6. 已知直三棱柱中，，，，‎ 则异面直线与所成角的余弦值为( ). ‎ ‎ ‎ A. B. C. D. ‎ ‎7. 执行如图所示的程序框图，若输出的n＝9，则输入的整数 p的最小值是（ ）‎ A．50 B．‎77 C．78 D．306‎ ‎8. 直线y＝kx＋1与圆x2＋y2＝1的位置关系是 ()‎ A．相交 B．相切 C．相交或相切 D．不能确定 l ‎9. 过点作圆的两条切线，切点分别为，则直线的方程为（ ）‎ A． B． C． D．‎ ‎10.某单位有技工18人，技术员12人，工程师6人，需要从这些人中抽取一个容量为的样本；如果采用系统抽样和分层抽样方法抽取，都不用剔除个体；如果容量增加一个，则在采用系统抽样时，需要从总体中剔除1个个体，则样本容量为（ ）‎ Ａ．4 Ｂ．5 Ｃ．6 Ｄ．无法确定 ‎11. ．在三棱锥P﹣ABC中，△ABC为等边三角形，PA⊥平面ABC，且PA=AB，则二面角A﹣PB﹣C的平面角的正切值为（ ）‎ A． B． C． D． ‎ ‎12.当曲线与直线有两个相异的交点时，实数的取值范围是（ ）‎ A. B. C. D.‎ 二. 填空题（共4小题，20分）‎ ‎13．已知集合A={（x，y）|y= 5x }，B={（x，y）|x2 + y2 = 5 }，则集合A∩B中元素的个数为 ． ‎ ‎14．某地区有农民、工作、知识分子家庭共计2004户，其中农民家庭1600户，工人家庭303户．现要从中抽出容量为40的样本，则在整个抽样过程中，可以用到下列抽样方法中的 ‎ ．（将你认为正确的序号都写上）‎ ① 简单随机抽样；②系统抽样；③分层抽样．‎ ‎15、已知圆，P是x轴上的动点，‎ PA、PB分别切圆C于A、B两点，则四边形CAPB的面积的最小值是____.‎ ‎16．如图，正方体ABCD﹣A1B‎1C1D1，则下列四个命题：‎ ‎① P在直线BC1上运动时，三棱锥A﹣D1PC的体积不变；‎ ‎② P在直线BC1上运动时，直线AP与平面ACD1所成角的大小不变； ③ P在直线BC1上运动时，二面角P﹣AD1﹣C的大小不变；‎ ‎④ M是平面A1B‎1C1D1上到点D和C1距离相等的点，则M点的轨迹是过D1点的直线；‎ 其中正确的命题编号是 ．‎ 三. 解答题（共6小题，70分）‎ ‎17．（本小题10分）直线l过点P（-- 1，3）．‎ ‎（1）若直线l的倾斜角为45°，求l的方程;‎ ‎（2）若直线与x轴、y轴交于A、B两点，求的面积．‎ ‎ ‎ ‎ ‎ ‎18．（本小题12分）‎ 已知三角形ABC的顶点坐标为A（0，3），B（﹣2，1），C（4，3），M是BC边上的中点．‎ ‎（1）求BC边的中线所在的直线方程；‎ ‎（2）求点C关于直线AB对称点C’的坐标．‎ ‎ ‎ ‎ ‎ ‎19. （本小题12分）‎ 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD． （1）求证：PA⊥CD；‎ ‎（2）若PA=PD= AD，求证：平面PAB⊥平面PCD ． ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎20.（本小题12分）‎ 如图在侧棱垂直底面的三棱柱中，、分别是和的中点.‎ ‎（1）证明：平面；‎ ‎（2）设，，求三棱锥的体积. ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎21.（本小题12分）‎ 已知圆心在直线y = 4x上，且与直线l：x + y - 2 = 0相切于点P（1，1）‎ ‎（1）求圆的方程.‎ ‎（2）直线kx - y + 3 = 0与该圆相交于A、B两点，若点M在圆上，且有向量(O为坐标原点)，求实数k.‎ ‎ ‎ ‎22. （本小题12分）‎ 已知圆O：，直线.‎ ‎（1）若直线l与圆O交于不同的两点A，B，当∠AOB =时，求k的值.‎ ‎（2）若，P是直线l上的动点，过P作圆O的两条切线PC、PD，切点为C、D，探究：直线CD是否过定点；‎ ‎（3）若EF、GH为圆O：的两条相互垂直的弦，垂足为M（1，），求四边形EGFH的面积的最大值.‎ ‎ ‎ 烈面中学高2018级高二上期中期考试试题 文 科 数 学 答案 一.选择题：‎ ‎1‎-5 C B C A B 6-10 B D C A C 11‎-12 A D ‎ ‎ 二． 填空题 ‎13．2 14. ①②③ 15. 16. ①③④‎ 三. 解答题（共6小题，70分）‎ ‎17．‎ ‎18．解：（1）x+y-3=0‎ ‎（2）设点C关于直线AB对称点C′的坐标为（a，b），‎ 则AB为线段CC′的垂直平分线，‎ 由直线AB的方程为：x﹣y+3=0，‎ 故，‎ 解得：a=0，b=7，‎ 即点C关于直线AB对称点C′的坐标为C’（0，7）‎ ‎ ‎ ‎19. 解：（1）证明：因为平面PAD⊥底面ABCD， 且平面PAD∩平面ABCD=AD， 又CD⊥AD，所以CD⊥面PAD． 又因为PA⊂平面PAD， 所以CD⊥PA．故PA⊥CD．…‎ ‎（2）证明：在△PAD中，因为， 所以PA⊥PD． 由（Ⅱ）可知PA⊥CD，且CD∩PD=D， 所以PA⊥平面PCD． 又因为PA⊂平面PAB， 所以面PAB⊥平面PCD． 20. 解：（I）连结交于点，连结.‎ 由题知，分别为，中点，所以.‎ ‎ ,.‎ ‎（II）在直三棱柱中，.‎ 又，为的中点，所以.‎ 又，.‎ ‎ ，，，‎ ‎，故，.‎ 所以.‎ ‎21.解：（1）设圆的方程为 因为直线相切，圆心到直线的距离，且圆心与切点连线与直线l垂直 可得a=0，r=，所以圆的方程为：…………………6分 ‎(2)直线与圆联立：，‎ 得：，‎ Δ=,解得.‎ 设A() B()，,‎ M()代入圆方程：‎ ‎，求得k=……………………………………12分 ‎ ‎ ‎ 22.解：（1）点O到的距离 ‎ ‎∴ =· ‎ ‎（2）由题意可知：O、P、C、D四点共圆且在以OP为直径的圆上，设 其方程为：‎ 即：‎ 又C、D在圆O：上 ‎∴ 即 ‎ 由 得 ‎ ‎∴直线CD过定点 ‎ ‎（3）设圆心O到直线EF、GH的距离分别为.‎ 则 ‎ ‎∴ ‎ ‎∴‎ 当且仅当 即 时，取“=”‎ ‎∴四边形EGFH的面积的最大值为 ‎ ‎ ‎ ‎