2020届 二轮复习 集合、简易逻辑与不等式 作业

2020届 二轮复习 集合、简易逻辑与不等式 作业

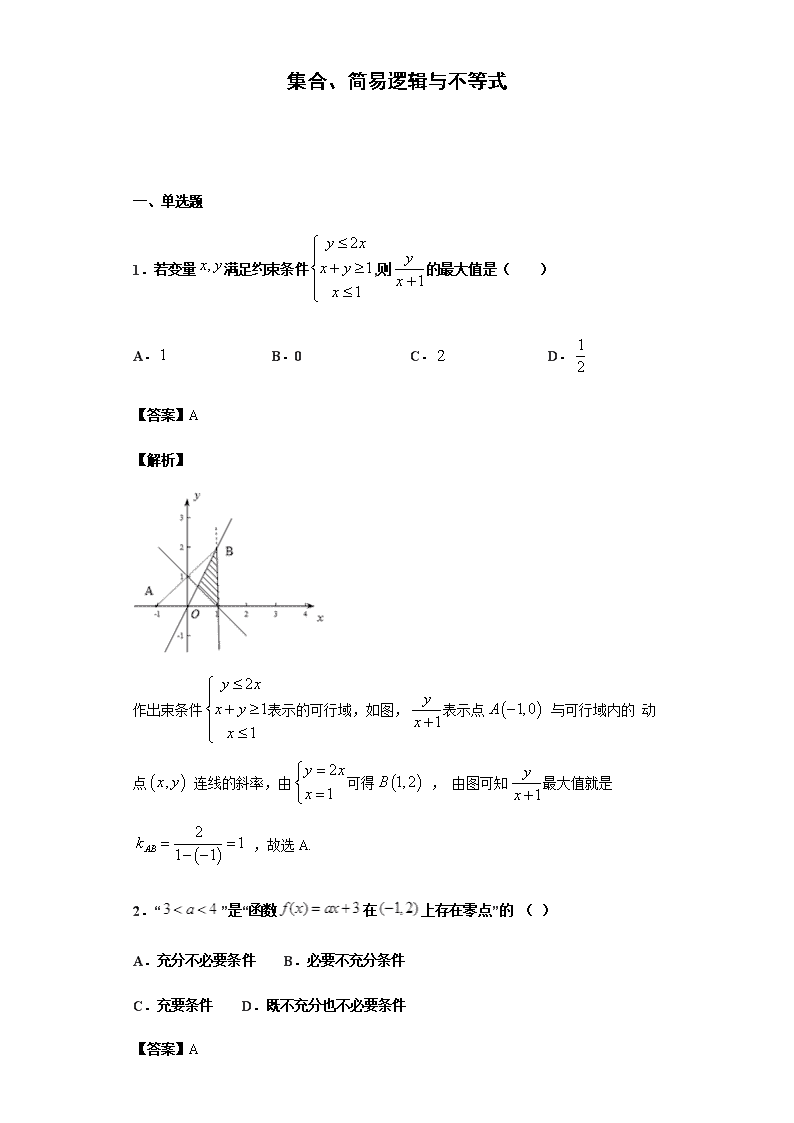
集合、简易逻辑与不等式 一、单选题 ‎1．若变量满足约束条件,则的最大值是（ ）‎ A． B．0 C． D．‎ ‎【答案】A ‎【解析】‎ 作出束条件表示的可行域，如图，表示点 与可行域内的 动点 连线的斜率，由可得 ， 由图可知最大值就是 ，故选A.‎ ‎2．“”是“函数在上存在零点”的 （ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】A ‎【解析】‎ 试题分析：“函数在上存在零点”或，故选A．‎ 考点：充要条件的判断.‎ ‎3．设全集U是实数集R，如下图所示，则阴影部分所表示的集合为(　　)‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 图中阴影部分表示的集合中的元素是在集合中，又在集合中，即，又，∴图中阴影部分表示的集合是：，故选A.‎ ‎4．集合，集合，则（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据集合的交集的概念及运算，即可求解，得到答案.‎ ‎【详解】‎ 因为，，由集合的交集运算可得，‎ 故选D.‎ ‎【点睛】‎ 本题主要考查了集合表示方法，以及集合交集的运算，其中解答中熟记集合的交集的概念及运算是解答的关键，着重考查了运算与求解能力，属于容易题.‎ ‎5．已知实数满足约束条件，若的最大值为1，则实数的值为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 如图画出可行域，当时，目标函数才有最大值，根据选项可得，而目标函数，斜率为3，所以函数过点时函数取得最大值， ，解得 ，所以，解得：，故选C.‎ ‎6．设，满足约束条件则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 画出约束条件的可行域，利用目标函数的最优解求解目标函数的范围即可．‎ ‎【详解】‎ x，y满足约束条件的可行域如图：‎ 目标函数z＝x+y，经过可行域的A，O时，目标函数取得最值，‎ 由解得A（0，3），‎ 目标函数z＝x+y的最大值为：0+3=3，最小值为：0，‎ 目标函数z＝x+y的取值范围：[0，3]．‎ 故选：D．‎ ‎【点睛】‎ 本题考查线性规划的简单应用，目标函数的最优解以及可行域的作法是解题的关键．‎ ‎7．在中，角，，所对应的边分别为，，，则“”是“”的（ ）‎ A．充分非必要条件 B．充分必要条件 C．必要非充分条件 D．非充分非必要条件 ‎【答案】B ‎【解析】‎ 试题分析：由正弦定理可知，中，均小于，所对应的边分别为，都是正数，“”“”，所以是充分必要条件；故选B．‎ 考点：正弦定理 ‎8．若集合，，则（ ）‎ A． B． C． D．‎‎(−2,5]‎ ‎【答案】D ‎【解析】‎ 试题分析：由题意A={x|10‎或者ax‎2‎+bx+c<0‎的解集，都跟它对应的一元二次方程ax‎2‎+bx+c=0‎的根有关，所以本题可以利用题目所给的一元二次不等式的解集，和韦达定理，求得a‎1‎‎,d的值.‎ ‎19．已知集合，，且，求实数的值.‎ ‎【答案】0或 ‎【解析】‎ ‎【分析】‎ 根据题意，分别讨论，两种情况，即可得出结果.‎ ‎【详解】‎ 因为集合，，且，‎ ‎∴‎ 若，解得；‎ 若，解得或（舍）；‎ 综上，实数的值为0或.‎ ‎【点睛】‎ 本题主要考查由集合间包含关系求参数，熟记集合间的基本关系，灵活运用分类讨论的思想即可求解，属于基础题型.‎ ‎20．已知集合是关于的不等式的解集，且中的一个元素是0，求实数的取值范围，并用表示出该不等式的解集．‎ ‎【答案】若，不等式的解集为；若，不等式的解集为.‎ ‎【解析】‎ ‎【分析】‎ 将已知不等式因式分解化为,将代入可解得 的范围,然后按照,分两种情况讨论可解得.‎ ‎【详解】‎ 由不等式因式分解可得:，‎ 由方程，可得两个根分别为：，．‎ 由适合不等式，故得，‎ ‎∴，或．‎ 若,则,所以 此时不等式的解集为．‎ 若，则,所以，此时不等式的解集为．‎ 综上所述: 若，不等式的解集为；若，不等式的解集为.‎ ‎【点睛】‎ 本题考查了一元二次不等式的解法,属于中档题.‎ ‎21．已知函数，且为常数.‎ ‎（1）当时，求的解集；‎ ‎（2）当，恒有，求实数的取值范围.‎ ‎（3）若在上有解，求实数a的取值范围.‎ ‎【答案】（1）；（2）；（3）.‎ ‎【解析】‎ ‎【分析】‎ ‎(1)令代入原式化简成二次函数的形式再进行求解即可.‎ ‎(2)参变分离有,故求在区间上的最小值即可.‎ ‎(3)参变分离后有故求在区间上的最大值即可.‎ ‎【详解】‎ ‎(1) 令,则当时,有或.‎ 因为,所以.‎ ‎(2)当时令.恒有即恒有在上恒成立.因为在上单调递增,故.‎ 故.‎ ‎(3)同(2)有在上有解.因为在上单调递减,‎ 故.故 ‎【点睛】‎ 本题主要考查了有关二次函数的复合函数问题,需要换元进行求解,同时也考查了在区间上恒成立与能成立问题,参变分离求最值即可.属于中等题型.‎ ‎22．设命题：函数的定义域为；命题：关于的方程有实根.‎ ‎（1）如果是真命题，求实数的取值范围.‎ ‎（2）如果命题“”为真命题，且“”为假命题，求实数的取值范围.‎ ‎【答案】(1) 实数的取值范围为;(2) 实数的取值范围是或.‎ ‎【解析】‎ ‎【详解】‎ 试题分析：（1）由函数的定义域为可得，可得实数的取值范围为；（2）化简命题可得，由为真命题，为假命题，可得一真一假，分两种情况讨论，对于真假以及假真分别列不等式组，分别解不等式组，然后求并集即可求得实数的取值范围.‎ 试题解析：（1）若命题是真命题，则有①当时定义域为，不合题意 ‎②当时，由已知可得 故所求实数的取值范围为 ‎（2）若命题是真命题，则关于的方程有实根，令，‎ ‎ ∴‎ 若命题“”为真命题，且“”为假命题，则一真一假 若真假，则；若假真，则 综上：实数的取值范围是或.‎