- 2021-06-11 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学:三-1《相似三角形的判定》测试3(新人教A版选修4-1)
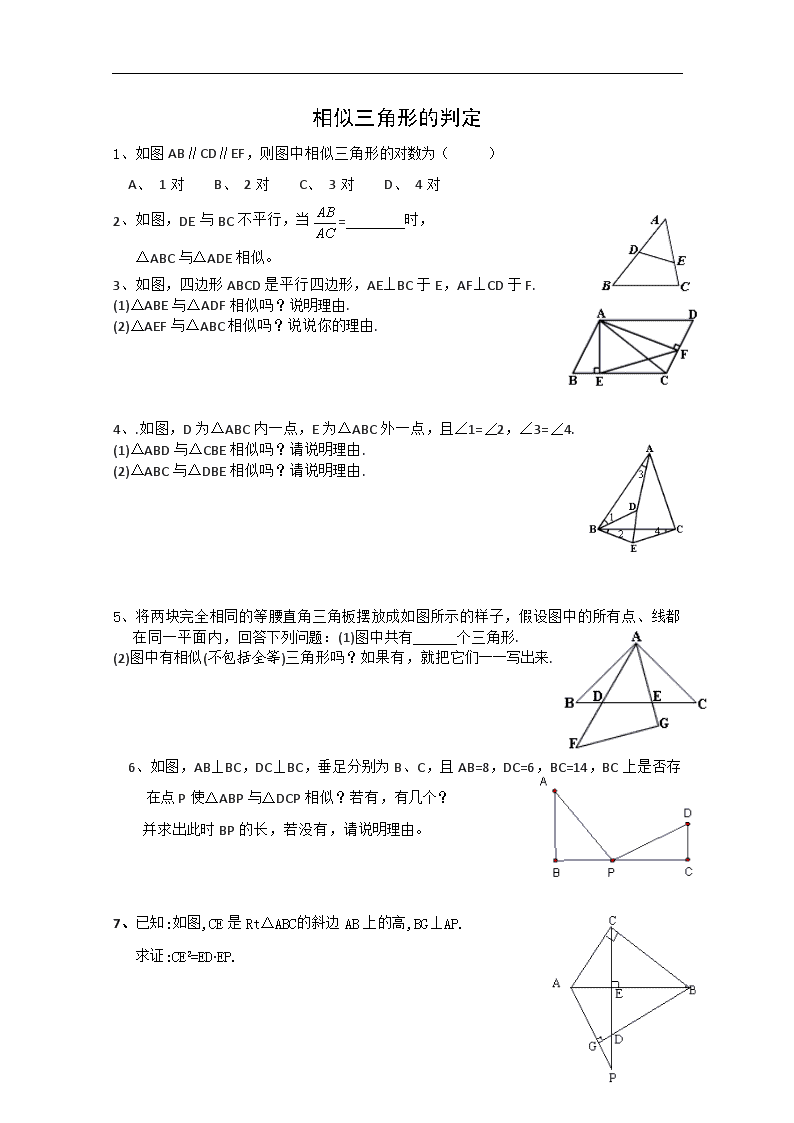
相似三角形的判定 1、如图AB∥CD∥EF,则图中相似三角形的对数为( ) A、 1对 B、 2对 C、 3对 D、 4对 2、如图,DE与BC不平行,当= 时, ΔABC与ΔADE相似。 3、如图,四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F. (1)ΔABE与ΔADF相似吗?说明理由. (2)ΔAEF与ΔABC相似吗?说说你的理由. 4、.如图,D为ΔABC内一点,E为ΔABC外一点,且∠1=∠2,∠3=∠4. (1)ΔABD与ΔCBE相似吗?请说明理由. (2)ΔABC与ΔDBE相似吗?请说明理由. 5、将两块完全相同的等腰直角三角板摆放成如图所示的样子,假设图中的所有点、线都在同一平面内,回答下列问题:(1)图中共有 个三角形. (2)图中有相似(不包括全等)三角形吗?如果有,就把它们一一写出来. 6、如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个? 并求出此时BP的长,若没有,请说明理由。 7、已知:如图,CE是RtΔABC 的斜边AB上的高,BG⊥AP. 求证:CE2=ED ·EP. D C P A B 8、.如图,在直角梯形ABCD中,AB//CD,,在AD上能否找到一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长。若不能,说明理由。 9、如图:AB是等腰直角三角形ABC的斜边,点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在AB上,设其落点为P, C M N A P B ①当P是边AB中点时,求证:; ②当P不是边AB中点时,是否仍成立?请证明你的结论; w.w.w.k.s.5.u.c.o.m www.ks5u.com查看更多