- 2021-06-11 发布 |
- 37.5 KB |
- 34页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习柱体、椎体、台体的表面积与体积课件(34张)(全国通用)
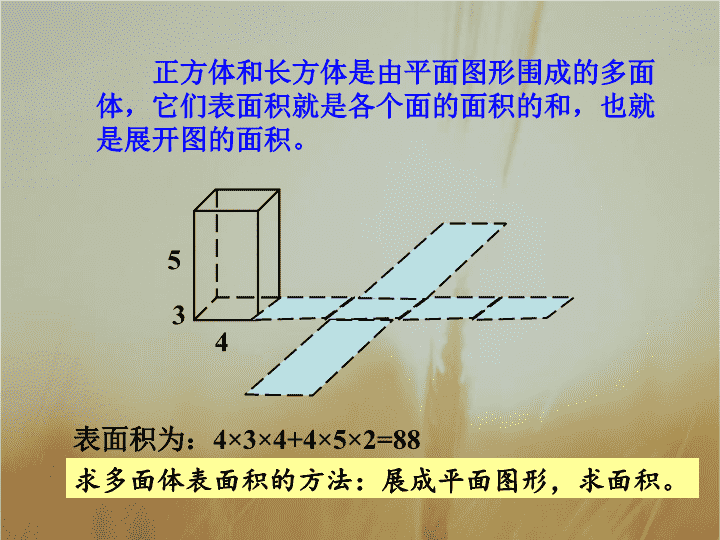
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗? 正方体和长方体是由平面图形围成的多面体,它们表面积就是各个面的面积的和,也就是展开图的面积。 5 4 3 表面积为: 4 ×3×4+4×5×2=88 求多面体表面积的方法:展成平面图形,求面积 。 柱体、锥体、台体的 表面积与体积 探究 棱柱、棱锥、棱台的展开图是什么? 棱柱的展开图是平行四边形 。 1. 柱体、锥体、台体的表面积 棱锥的展开图是三角形 。 同理,棱台的展开图呢? 棱台的展开图是梯形 。 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的 表面积就是计算它的各个侧面面积和底面面积之和。 已知棱长为 a ,各面均为等边三角形的四面体 S-ABC ,求它的表面积 。 D B C A S 分析: 四面体的展开图是由四个全等的正三角形组成。 因为 BC=a , 所以: 因此,四面体 S-ABC 的表面积: 解: 先求 ΔSBC 的面积,过 S 做 SD⊥BC , 交 BC 于点 D 。 例一 圆柱、圆锥、圆台是旋转体,它们的展开图是什么样的呢? 思考 圆柱 是 以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。 圆柱的侧面展开图是矩形。 视频:圆柱的侧面积 圆锥 是以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体。 圆锥的侧面展开图是扇形。 圆台 是以直角梯形的垂直边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。 圆台的侧面展开图是 扇环。 一个圆台形花盆盆口直径 20 cm ,盆底直径为 15cm ,底部渗水圆孔直径为 1.5 cm ,盆壁长 15cm 。那么花盆的表面积约是多少平方厘米( π 取 3.14 ,结果精确到 1 cm 2 )? 解: 由圆台的表面积公式得 花盆的表面积: 答:花盆的表面积约是 999 . 例二 r' = r 上底扩大 r' = 0 上底缩小 探究 圆柱、圆锥、圆台三者的表面积公式之间有什么关系? 2. 柱体、椎体、台体的体积 我们已经学习了特殊的棱柱 —— 正方体、长方体以及圆柱的体积公式 , 它们的体积公式可以统一为: ( S 为底面面积, h 为高) 一般柱体体积也是: 其中 S 为底面面积, h 为棱柱的高。 圆锥的体积公式: ( 其中 S 为底面面积, h 为高 ) 棱锥的体积公式: ( 其中 S 为底面面积, h 为高 ) 圆锥体积等于同底等高的圆柱的体积的 棱锥体积等于同底等高的棱柱的体积的 由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是等于底面面积乘高的 。 探究 如何求台体的体积? 由于圆台 ( 棱台 ) 是由圆锥 ( 棱锥 ) 截成的,因此用两个锥体的体积差。得到圆台 ( 棱台 ) 的体积公式 : 其中 S , S‘ 分别为上、下底面面积, h 为圆台(棱台)的高。 上底扩大 上底缩小 圆柱、圆锥、圆台三者的体积公式之间有什么关系? 资料包:棱台 - 圆台的体积 有一堆规格相同的铁制(铁的密 是 )六角螺帽共重 5.8kg ,已知底面是正六边形,边长为 12mm ,内孔直径为 10mm ,高为 10mm ,问这堆螺帽大约有多少个( π 取 3.14 )? 例三 解: 六角螺帽的体积是六棱柱的体积与圆柱体积之差, 即 : 所以螺帽的个数为 (个) 答:这堆螺帽大约有 252 个. 课堂小结 r ’ = r 上底扩大 r ’ = 0 上底缩小 柱体、椎体、台体的表面积: 上底扩大 上底缩小 柱体、椎体、台体的体积: 高考链接 1. ( 2009 山东)一空间几何体的三视图如图所示,则该几何体的体积为( ) 俯视图 2 2 2 正 ( 主 ) 视图 2 2 侧 ( 左 ) 视图 A. B. C. D. C 【 解析 】: 该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为 1, 高为 2, 体积为 , 四棱锥的底面边长为 ,高为 所以体积为: 所以该几何体的体积为: 2. ( 2009 辽宁)设某几何体的三视图(单位 :cm )如图所示,(尺寸的长度单位为 m ) . 则该几何体的体积为 __________ 。 3 4 m 3 正视图 侧视图 俯视图 【 解析 】 由三视图知其为三棱锥,由“主左一样高,主俯一样长,俯左一样宽”可知高为 2 ,地面三角形的底面边长为 4 ,高为 3 ,则所求棱锥体积为: 课堂练习 1 . 圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是_______ 。 4πS 2 . 已知圆锥的表面积为 a ㎡ ,且它的侧面展开图是一个半圆,则这圆锥的底面直径为 ______________ 。 3. 若圆台的上、下底面半径分别是 1 和 3 , 它的侧面积是两底面积和的 2 倍,则圆台的母线长为 ___________ . 5 4 . 若一个圆柱的侧面展开图是一个正方形, 则这个圆柱的全面积与侧面积的比是 ( ) A . B . C . D . A 5 . 已知圆锥的全面积是底面积的 3 倍,那么这个 圆锥的侧面积展开图-扇形的圆心角为 _______ 度 。 180 6.如图 , 已知 : 三棱锥 A-BCD 的侧棱 AD 垂直于底面 BCD, 侧面 ABC 与底面所成的角为 θ 。 求证 : V 三棱锥 = ⅓ S Δ ABC · ADcos θ 。 证明 : 在平面 BCD 内,作 DE⊥BC , 垂足为 E , 连结 AE,DE 就是 AE 在平面 BCD 上的射影。 根据三垂线定理, AE⊥BC 。 ∴∠AED= θ V 三棱锥 = ⅓ S Δ ABC×AD = ⅓ × ½ ×BC × ED × AD = ⅓ × ½ ×BC.AE × cos θ × AD = ⅓ S Δ ABCADcos θ A D C E B θ 习题答案 1. 2. 1.74千克。查看更多