- 2021-06-11 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版立体几何综合问题作业
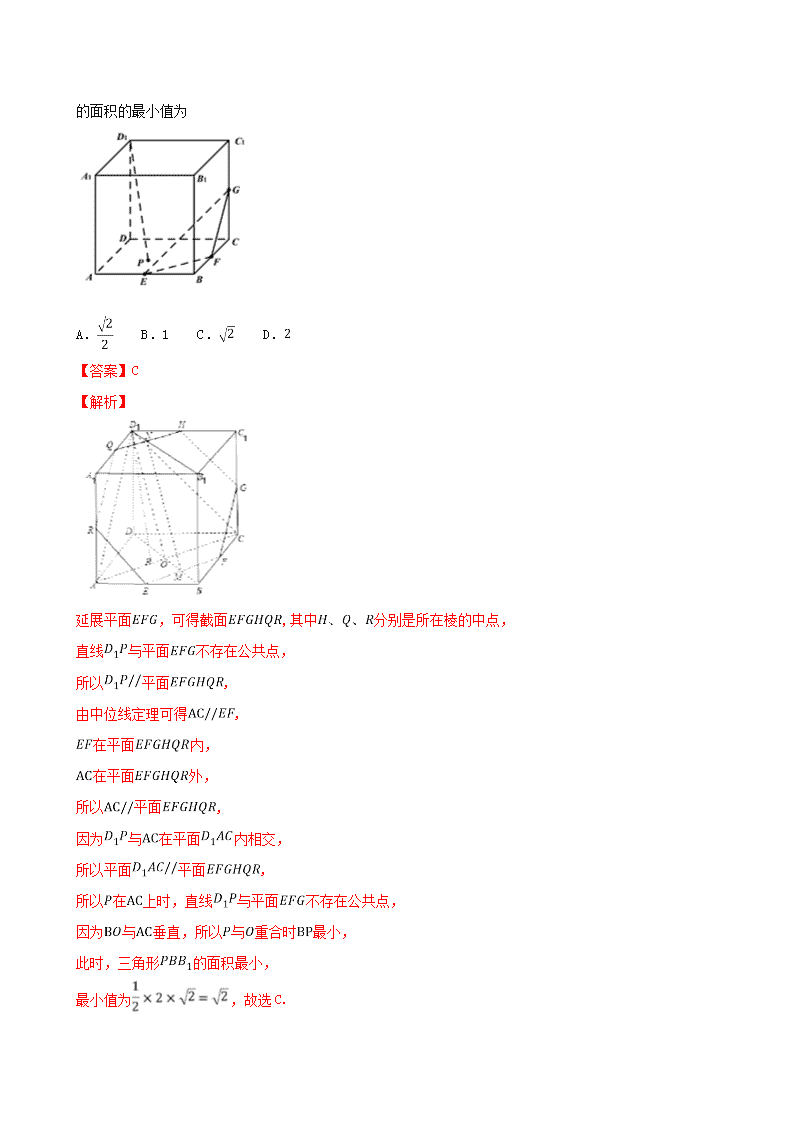
立体几何综合问题 1.【湖北省荆门市2019届高三月考】在棱长为4的正方体中,是中点,点是正方形内的动点(含边界),且满足,则三棱锥的体积最大值是( ) A. B. C. D. 【答案】D 【解析】因为在棱长为4的正方体中,是中点,点是正方形内的动点(含边界),且满足, 所以, 所以,即 , 令点P在DC上的投影点为O,,, 所以, 整理得, 根据函数单调性可得当时,有最大值为16,所以 的最大值为, 因为, 所以三棱锥体积最大值为:,故选D。 2.【江西省南昌市2018届测试】如图,在正四棱台中,上底面边长为4,下底面边长为8,高为5,点分别在上,且.过点的平面与此四棱台的下底面会相交,则平面与四棱台的面的交线所围成图形的面积的最大值为 A. B. C. D. 【答案】B 【解析】当斜面α经过点时与四棱台的面的交线围成的图形的面积最大,此时α为等腰梯形,上底为MN=4,下底为BC=8此时作正四棱台俯视图如下: 则MN中点在底面的投影到BC的距离为8-2-1=5 因为正四棱台的高为5,所以截面等腰梯形的高为 所以截面面积的最大值为 所以选B 3.【湖南省益阳市2019届高三上学期期末】直三棱柱外接球表面积为,,若,矩形外接圆的半径分别为,则的最大值为( ) A. B.3 C. D. 【答案】C 【解析】由外接球表面积为,可得外接球半径为2.设中点为,,矩形外接圆的圆心分别为,球心为,则由平面与平面得为矩形,, , ,,当且仅当时取等号. 故选. 4.【北京市丰台区2019届高三第一学期期末】如图,在棱长为2的正方体中,分别是棱的中点,是底面内一动点,若直线与平面不存在公共点,则三角形 的面积的最小值为 A. B.1 C. D. 【答案】C 【解析】 延展平面,可得截面,其中分别是所在棱的中点, 直线与平面不存在公共点, 所以平面, 由中位线定理可得, 在平面内, 在平面外, 所以平面, 因为与在平面内相交, 所以平面平面, 所以在上时,直线与平面不存在公共点, 因为与垂直,所以与重合时最小, 此时,三角形的面积最小, 最小值为,故选C. 5.(2018·黄冈模拟)如图,在多面体ABCDEF中,平面ABCD为正方形,AB=2,AE=3,DE=,二面角E-AD-C的余弦值为,且EF∥BD. (1)证明:平面ABCD⊥平面EDC. (2)求平面AEF与平面EDC夹角的余弦值. 【解析】(1)因为AB=AD=2,AE=3,DE=, 所以AD2+DE2=AE2,所以AD⊥DE. 又因为在正方形ABCD中,AD⊥DC, 且DE∩DC=D, 所以AD⊥平面EDC, 又因为AD平面ABCD, 所以平面ABCD⊥平面EDC. (2)由(1)知∠EDC是二面角E-AD-C的平面角,作OE⊥CD于点O, 则OD=DE·cos∠EDC=1,OE=2, 且平面ABCD⊥平面EDC, 平面ABCD∩平面EDC=CD,OE平面EDC, 所以OE⊥平面ABCD, 取AB中点M,连接OM,则OM⊥CD,如图,建立空间直角坐标系, 则A(2,-1,0),B(2,1,0),D(0,-1,0),C(0,1,0),E(0,0,2), 所以=(-2,1,2),=(2,2,0), 由EF∥BD,知EF的一个方向向量为(2,2,0), 设平面AEF的法向量为n=(x,y,z), 则 取x=-2,得n=(-2,2,-3), 因为平面EDC的一个法向量为m=(2,0,0), 所以cos查看更多