2021届高考数学一轮复习第九章平面解析几何第4节直线与圆圆与圆的位置关系课件新人教A版

2021届高考数学一轮复习第九章平面解析几何第4节直线与圆圆与圆的位置关系课件新人教A版

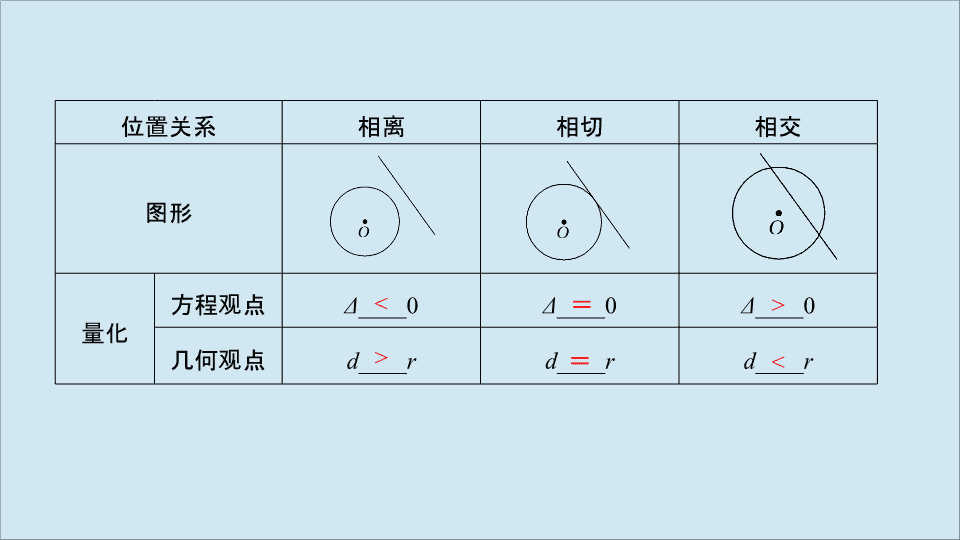
第 4 节　直线与圆、圆与圆的位置关系 考试要求　 1. 能根据给定直线、圆的方程判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆的位置关系； 2. 能用直线和圆的方程解决一些简单的问题； 3. 初步了解用代数方法处理几何问题的思想 . 知 识 梳 理 1. 直线与圆的位置关系 位置关系 相离 相切 相交 图形 量化 方程观点 Δ ____0 Δ ____0 Δ ____0 几何观点 d ____ r d ____ r d ____ r < ＝ > > ＝ < 2. 圆与圆的位置关系 设两圆的半径分别为 R ， r ( R ＞ r ) ，两圆圆心间的距离为 d ，则两圆的位置关系可用下表表示： 位置关系 外离 外切 相交 内切 内含 图形 量的关系 __________ _________ __________ __________ ________ _________ 公切线条数 4 3 2 1 0 d ＞ R ＋ r d ＝ R ＋ r R － r ＜ d ＜ R ＋ r d ＝ R － r d ＜ R － r [ 常用结论与微点提醒 ] 1. 圆的切线方程常用结论 (1) 过圆 x 2 ＋ y 2 ＝ r 2 上一点 P ( x 0 ， y 0 ) 的圆的切线方程为 x 0 x ＋ y 0 y ＝ r 2 . (2) 过圆 ( x － a ) 2 ＋ ( y － b ) 2 ＝ r 2 上一点 P ( x 0 ， y 0 ) 的圆的切线方程为 ( x 0 － a )( x － a ) ＋ ( y 0 － b )( y － b ) ＝ r 2 . (3) 过圆 x 2 ＋ y 2 ＝ r 2 外一点 M ( x 0 ， y 0 ) 作圆的两条切线，则两切点所在直线方程为 x 0 x ＋ y 0 y ＝ r 2 . 2. 直线被圆截得的弦长的求法 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) “ k ＝ 1 ” 是 “ 直线 x － y ＋ k ＝ 0 与圆 x 2 ＋ y 2 ＝ 1 相交 ” 的必要不充分条件 .( 　　 ) (2) 如果两个圆的方程组成的方程组只有一组实数解，则两圆外切 .( 　　 ) (3) 如果两圆的圆心距小于两圆的半径之和，则两圆相交 .( 　　 ) (4) 过圆 O ： x 2 ＋ y 2 ＝ r 2 外一点 P ( x 0 ， y 0 ) 作圆的两条切线，切点分别为 A ， B ，则 O ， P ， A ， B 四点共圆且直线 AB 的方程是 x 0 x ＋ y 0 y ＝ r 2 .( 　　 ) 解析 　 (1) “ k ＝ 1 ” 是 “ 直线 x － y ＋ k ＝ 0 与圆 x 2 ＋ y 2 ＝ 1 相交 ” 的充分不必要条件； (2) 除外切外，还有可能内切； (3) 两圆还可能内切或内含 . 答案　 (1) × 　 (2) × 　 (3) × 　 (4) √ 2. ( 老教材必修 2P132A5 改编 ) 直线 l ： 3 x － y － 6 ＝ 0 与圆 x 2 ＋ y 2 － 2 x － 4 y ＝ 0 相交于 A ， B 两点，则 | AB | ＝ ______. 3. ( 老教材必修 2P133A9 改编 ) 圆 x 2 ＋ y 2 － 4 ＝ 0 与圆 x 2 ＋ y 2 － 4 x ＋ 4 y － 12 ＝ 0 的公共弦长为 ________. 4. (2019· 太原模拟 ) 若圆 C 1 ： x 2 ＋ y 2 ＝ 1 与圆 C 2 ： x 2 ＋ y 2 － 6 x － 8 y ＋ m ＝ 0 外切，则 m ＝ ( 　　 ) A.21 B.19 C.9 D. － 11 答案　 B 6. ( 多填题 ) (2019· 浙江卷 ) 已知圆 C 的圆心坐标是 (0 ， m ) ，半径长是 r . 若直线 2 x － y ＋ 3 ＝ 0 与圆 C 相切于点 A ( － 2 ，－ 1) ，则 m ＝ ________ ， r ＝ ________. 解析　 根据题意画出图形，可知 A ( － 2 ，－ 1) ， C (0 ， m ) ， B (0 ， 3) ， ∵ 直线 2 x － y ＋ 3 ＝ 0 与圆 C 相切于点 A ， ∴∠ BAC ＝ 90° ， ∴ | AB | 2 ＋ | AC | 2 ＝ | BC | 2 . 即 20 ＋ 4 ＋ ( m ＋ 1) 2 ＝ ( m － 3) 2 ，解得 m ＝－ 2. 考点一　直线与圆的位置关系　 多维探究 角度 1 　位置关系的判断 【例 1 － 1 】 在 △ ABC 中，若 a sin A ＋ b sin B － c sin C ＝ 0 ，则圆 C ： x 2 ＋ y 2 ＝ 1 与直线 l ： ax ＋ by ＋ c ＝ 0 的位置关系是 ( 　　 ) A. 相切 B. 相交 C. 相离 D. 不确定 答案　 A 规律方法　 判断直线与圆的位置关系的常见方法 (1) 几何法：利用 d 与 r 的关系 . (2) 代数法：联立方程之后利用 Δ 判断 . (3) 点与圆的位置关系法：若直线恒过定点且定点在圆内，可判断直线与圆相交 . 上述方法中最常用的是几何法，点与圆的位置关系法适用于动直线问题 . A.3 x ＋ 4 y － 12 ＝ 0 或 4 x － 3 y ＋ 9 ＝ 0 B.3 x － 4 y ＋ 12 ＝ 0 或 4 x ＋ 3 y ＋ 9 ＝ 0 C.4 x － 3 y ＋ 9 ＝ 0 或 x ＝ 0 D.3 x ＋ 4 y － 12 ＝ 0 或 x ＝ 0 答案　 D 【训练 1 】 (1) ( 角度 1)(2019· 西安八校联考 ) 若过点 A (3 ， 0) 的直线 l 与曲线 ( x － 1) 2 ＋ y 2 ＝ 1 有公共点，则直线 l 斜率的取值范围为 ( 　　 ) 考点二　圆的切线问题　 典例迁移 【例 2 】 ( 经典母题 ) 过点 P (2 ， 4) 引圆 C ： ( x － 1) 2 ＋ ( y － 1) 2 ＝ 1 的切线，则切线方程为 ________. 答案　 x ＝ 2 或 4 x － 3 y ＋ 4 ＝ 0 【迁移 2 】 在例 2 中，已知条件不变，设两个切点为 A ， B ，求切点弦 AB 所在的直线方程 . 解　由题意得，点 P ， A ， C ， B 在以 PC 为直径的圆上， 此圆的方程为 ( x － 2)( x － 1) ＋ ( y － 4)( y － 1) ＝ 0 ， 整理得 x 2 ＋ y 2 － 3 x － 5 y ＋ 6 ＝ 0 ， ① ， 圆 C ： ( x － 1) 2 ＋ ( y － 1) 2 ＝ 1 展开得 x 2 ＋ y 2 － 2 x － 2 y ＋ 1 ＝ 0 ， ② 由 ② － ① 得 x ＋ 3 y － 5 ＝ 0 ，即为直线 AB 的方程 . 【迁移 3 】 ( 多填题 ) 在例 2 中，已知条件不变，则切线 PA 的长度为 ________ ，弦 AB 的长度为 ________. 解析　 如图，在 Rt △ PAC 中， 规律方法　 求过某点的圆的切线问题时，应首先确定点与圆的位置关系，再求直线方程 . 若点在圆上 ( 即为切点 ) ，则过该点的切线只有一条；若点在圆外，则过该点的切线有两条，此时注意斜率不存在的切线 . 【训练 2 】 过直线 y ＝ 2 x ＋ 3 上的点作圆 C ： x 2 ＋ y 2 － 4 x ＋ 6 y ＋ 12 ＝ 0 的切线，则切线长的最小值为 ( 　　 ) 考点三　圆与圆的位置关系 【例 3 】 (2020· 贵阳调研 ) 已知两圆 x 2 ＋ y 2 － 2 x － 6 y － 1 ＝ 0 ， x 2 ＋ y 2 － 10 x － 12 y ＋ m ＝ 0. (1) m 取何值时两圆外切？ (2) m 取何值时两圆内切？ (3) 当 m ＝ 45 时，求两圆的公共弦所在直线的方程和公共弦的长 . 规律方法　 1. 判断两圆的位置关系时常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法 . 2. 若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差消去 x 2 ， y 2 项得到 . 答案　 B