- 2021-06-11 发布 |
- 37.5 KB |
- 8页
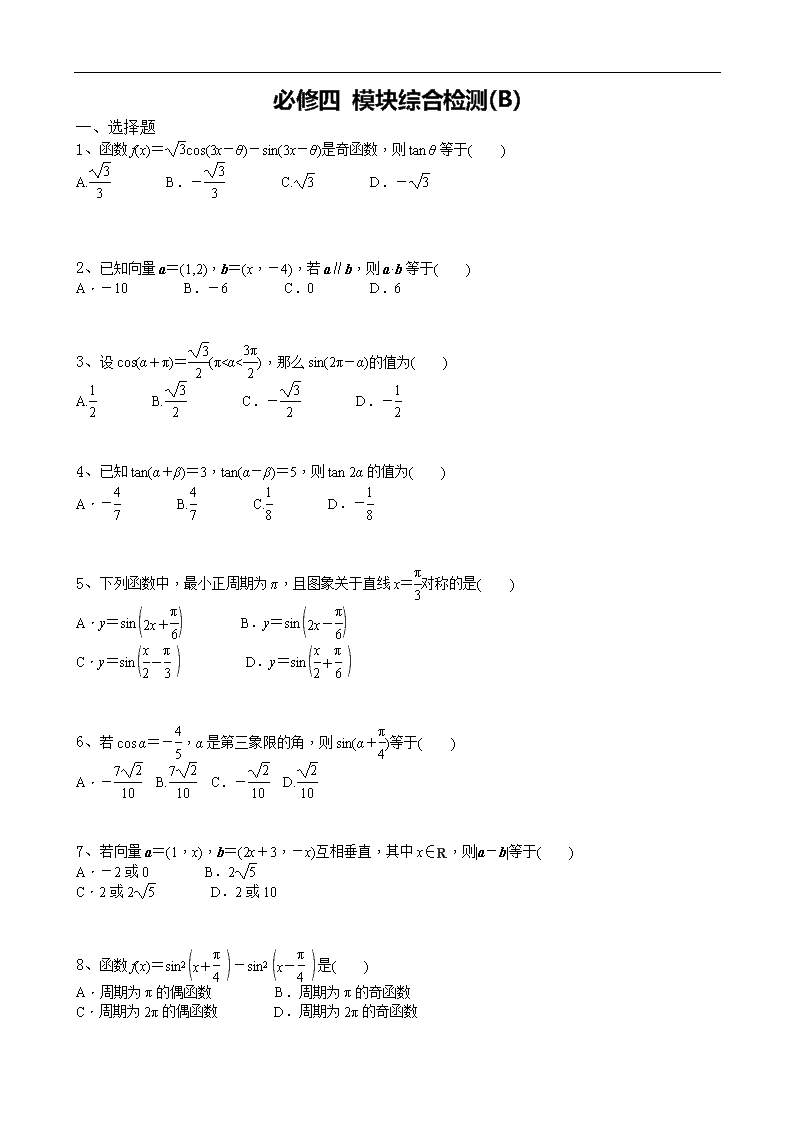


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修4同步练习:模块综合检测(B)
必修四 模块综合检测(B) 一、选择题 1、函数f(x)=cos(3x-θ)-sin(3x-θ)是奇函数,则tan θ等于( ) A. B.- C. D.- 2、已知向量a=(1,2),b=(x,-4),若a∥b,则a·b等于( ) A.-10 B.-6 C.0 D.6 3、设cos(α+π)=(π<α<),那么sin(2π-α)的值为( ) A. B. C.- D.- 4、已知tan(α+β)=3,tan(α-β)=5,则tan 2α的值为( ) A.- B. C. D.- 5、下列函数中,最小正周期为π,且图象关于直线x=对称的是( ) A.y=sin B.y=sin C.y=sin D.y=sin 6、若cos α=-,α是第三象限的角,则sin(α+)等于( ) A.- B. C.- D. 7、若向量a=(1,x),b=(2x+3,-x)互相垂直,其中x∈R,则|a-b|等于( ) A.-2或0 B.2 C.2或2 D.2或10 8、函数f(x)=sin2-sin2是( ) A.周期为π的偶函数 B.周期为π的奇函数 C.周期为2π的偶函数 D.周期为2π的奇函数 9、把函数f(x)=sin的图象向右平移个单位可以得到函数g(x)的图象,则g等于( ) A.- B. C.-1 D.1 10、已知sin α=,则cos 2α的值为( ) A.- B.- C. D. 11、已知|a|=2|b|≠0,且关于x的方程x2+|a|x+a·b=0有实根,则a与b的夹角的取值范围是( ) A. B. C. D. 12、已知向量a=(1,0),b=(cos θ,sin θ),θ∈[-,],则|a+b|的取值范围是( ) A.[0,] B.[0,) C.[1,2] D.[,2] 二、填空题 13、已知向量a=(3,1),b=(1,3),c=(k,2),若(a-c)⊥b,则k=________. 14、已知α为第二象限的角,sin α=,则tan 2α=________. 15、当0≤x≤1时,不等式sin≥kx成立,则实数k的取值范围是________. 16、如图,正六边形ABCDEF中,有下列四个命题: ①+=2; ②=2+2; ③·=·; ④(·)=(·). 其中真命题的序号是________.(写出所有真命题的序号) 三、解答题 17、已知a=(cos ωx,sin ωx),b=(2cos ωx+sin ωx,cos ωx),x∈R,ω>0,记f(x)=a·b,且该函数的最小正周期是. (1)求ω的值; (2)求函数f(x)的最大值,并且求使f(x)取得最大值的x的集合. 18、已知0查看更多
相关文章
- 当前文档收益归属上传用户