- 2021-06-11 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
新疆博尔塔拉蒙古自治州第五师高级中学2020届高三上学期月考数学(文)试题
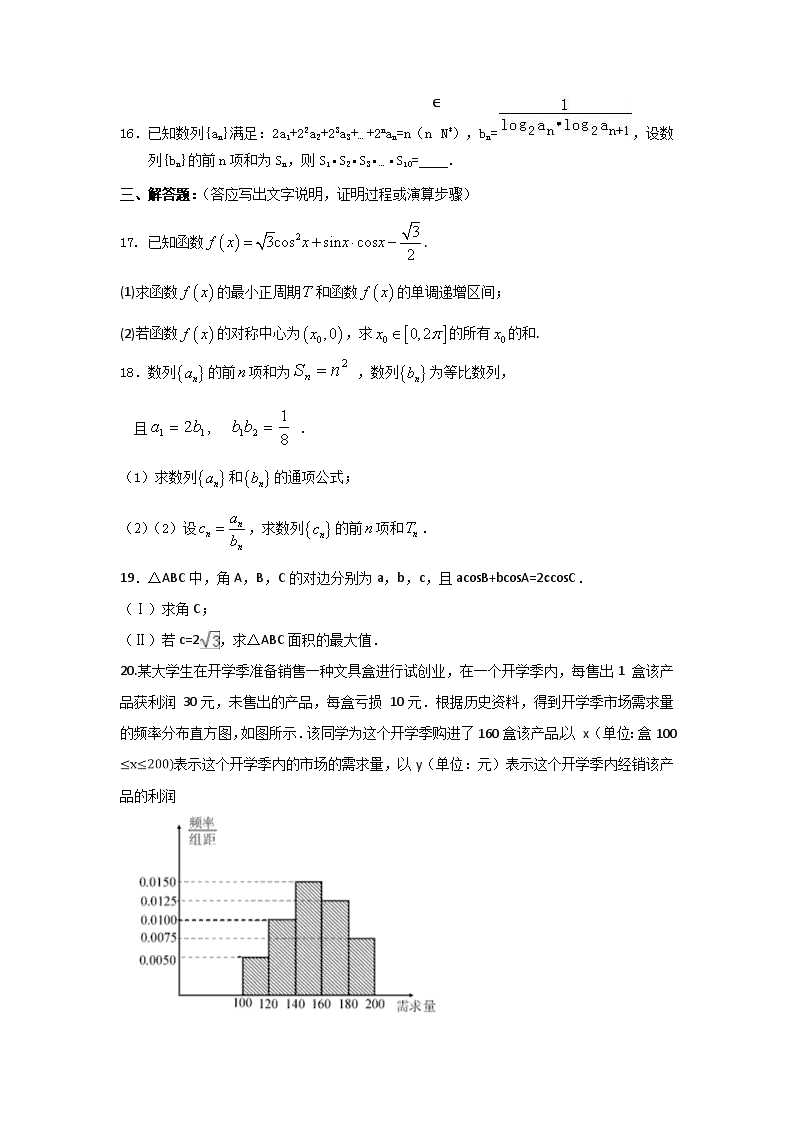
文数试卷 一、选择题:(大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.集合P={y|y=﹣x2+2},Q={x|y=﹣x+2}则P∩Q是( ) A.(0,2),(1,1) B.{(0,2),(1,1)} C.∅ D.{y|y≤2} 2.在复平面内,复数z=对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.已知平面向量, 的夹角为,且, ,则( ) A. 1 B. 2 C. D. 3 4.设等差数列{an}的前n项和为Sn,若S9=54,则a2+a4+a9=( ) A.9 B.15 C.18 D.36 5.若x=,则sin4x﹣cos4x的值为( ) A. B.﹣ C.﹣ D. 6.下列命题推断错误的是( ) A.命题“若x=y,则sinx=siny”的逆否命题为真命题 B.若p且q为假命题,则p,q均为假命题 C.“x=﹣1”是“x2﹣5x﹣6=0”的充分不必要条件 D.命题p:存在x0∈R,使得,则非p:任意x∈R,都有 7执行如图所示的程序框图,则输出的i的值为( ) A.5 B.6 C.7 D.8 8.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( ) A.96 B. C. D. 9..已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=( ) A. B. C.1 D.2 10.已知三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形,AB=2,SA=SB=SC=2,则三棱锥的外接球的球心到平面ABC的距离是( ) A. B.1 C. D. 11已知函数有两个零点,则的取值范围是( ) A. B. C. D. 12.已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>﹣2f(x),若g(x)=x2f(x),则不等式g(x)<g(1)的解集是( ) A.(﹣∞,1) B.(﹣∞,0)∪(0,1) C.(﹣1,1) D.(﹣1,0)∪(0,1) 二、填空题:(大题共4小题,每小题5分) 13.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽取10名学生,将这50名学生随机编号号,并分组,第一组号,第二组号,…,第十组,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为 ___ 14.已知函数f(x)是定义域为R的奇函数,当x∈[0,1]时,f(x)=log2(x+1),则f(1﹣)= . 15.函数的最大值是____. 16.已知数列{an}满足:2a1+22a2+23a3+…+2nan=n(n∈N*),bn=,设数列{bn}的前n项和为Sn,则S1•S2•S3•…•S10= . 三、解答题:(答应写出文字说明,证明过程或演算步骤) 17. 已知函数. (1)求函数的最小正周期和函数的单调递增区间; (2)若函数的对称中心为,求的所有的和. 18.数列的前项和为 ,数列为等比数列, 且 . (1) 求数列和的通项公式; (2) (2)设,求数列的前项和. 19.△ABC中,角A,B,C的对边分别为a,b,c,且acosB+bcosA=2ccosC. (Ⅰ)求角C; (Ⅱ)若c=2,求△ABC面积的最大值. 20.某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1 盒该产品获利润 30元,未售出的产品,每盒亏损 10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以 x(单位:盒100表示这个开学季内的市场的需求量,以y(单位:元)表示这个开学季内经销该产品的利润 (1)根据直方图估计这个开学季内市场需求量 x的众数和平均数; (2)将y表示为 x函数; (3)根据直方图估计利润y 不少于4000元的概率。 21.如图正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2. (Ⅰ)求证:AB⊥平面ADE; (Ⅱ)求凸多面体ABCDE的体积. 22.已知函数f(x)=a(x+1)2﹣4lnx,a∈R. (Ⅰ)若a=,求曲线f(x)在点(1,f(1))处的切线方程; (Ⅱ)若对任意x∈[1,e],f(x)<1恒成立,求实数a的取值范围. 数学试卷(文数)答案 (1) 选择题 1 2 3 4 5 6 7 8 9 10 11 12 D C C C C B B C B A D D (2) 填空题 13 37 14 -1/2 15 1 16 1/11 三.解答题17. 18. 19解:(Ⅰ)∵在△ABC中acosB+bcosA=2ccosC, ∴由正弦定理可得sinAcosB+sinBcosA=2sinCcosC, ∴sin(A+B)=2sinCcosC, ∴sinC=2sinCcosC, ∴解得:cosC=, ∴由三角形内角的范围可得角C=. (Ⅱ)由余弦定理可得:12=c2=a2+b2﹣2abcosC≥2ab﹣ab=ab, 可得ab≤12,当且仅当a=2时取等号. ∴△ABC面积的最大值==3. 20. 解:(1)由频率直方图得:最大需求量为的频率. 这个开学季内市场需求量的众数估计值是; 需求量为的频率, 需求量为的频率, 需求量为的频率, 需求量为的频率, 需求量为的频率. 则平均数. (2)因为每售出盒该产品获利润元,未售出的产品,每盒亏损元, 所以当时,, 当时,, 所以. (3)因为利润不少于元所以,解得,解得. 所以由(1)知利润不少于元的概率. 21证明:(Ⅰ)∵AE⊥平面CDE,CD⊂平面CDE, ∴AE⊥CD, 又在正方形ABCD中,CD⊥AD,AE∩AD=A, ∴CD⊥平面ADE, 又在正方形ABCD中,AB∥CD, ∴AB⊥平面ADE.… 解:(Ⅱ)连接BD,设B到平面CDE的距离为h, ∵AB∥CD,CD⊂平面CDE, ∴AB∥平面CDE,又AE⊥平面CDE, ∴h=AE=1,又=, ∴=, 又==, ∴凸多面体ABCDE的体积V=VB﹣CDE+VB﹣ADE=.… . 22. 解:(Ⅰ)由得f(1)=2…1 …3 则所求切线方程为y﹣2=﹣2(x﹣1),即y=﹣2x+4…4 (Ⅱ)…5 令g(x)=ax2+ax﹣2. 当a=0时,,f(x)在[1,e]上单调递减, [f(x)]max=f(1)=0<1,恒成立,符合题意…6 当a<0时,g(x)=ax2+ax﹣2,开口向下,对称轴为,且g(0)=﹣2<0, 所以当x∈[1,e]时,g(x)<0,f′(x)<0,f(x)在[1,e]上单调递减, [f(x)]max=f(1)=0<1,恒成立,符合题意…8 当a>0时,g(x)=ax2+ax﹣2的开口向上,对称轴为,g(0)=﹣2<0, 所以g(x)=ax2+ax﹣2在(0,+∞)单调递增,故存在唯一x0∈(0,+∞), 使得g(x0)=0,即f′(x0)=0…9 当0<x<x0时,g(x)<0,f′(x)<0,f(x)单调递减; 当x>x0时,g(x)>0,f′(x)>0,f(x)单调递增, 所以在[1,e]上,[f(x)]max=max{f(1),f(e)}. 所以,得,得.所以…11 综上,a得取值范围是…12查看更多