- 2021-06-11 发布 |
- 37.5 KB |
- 10页
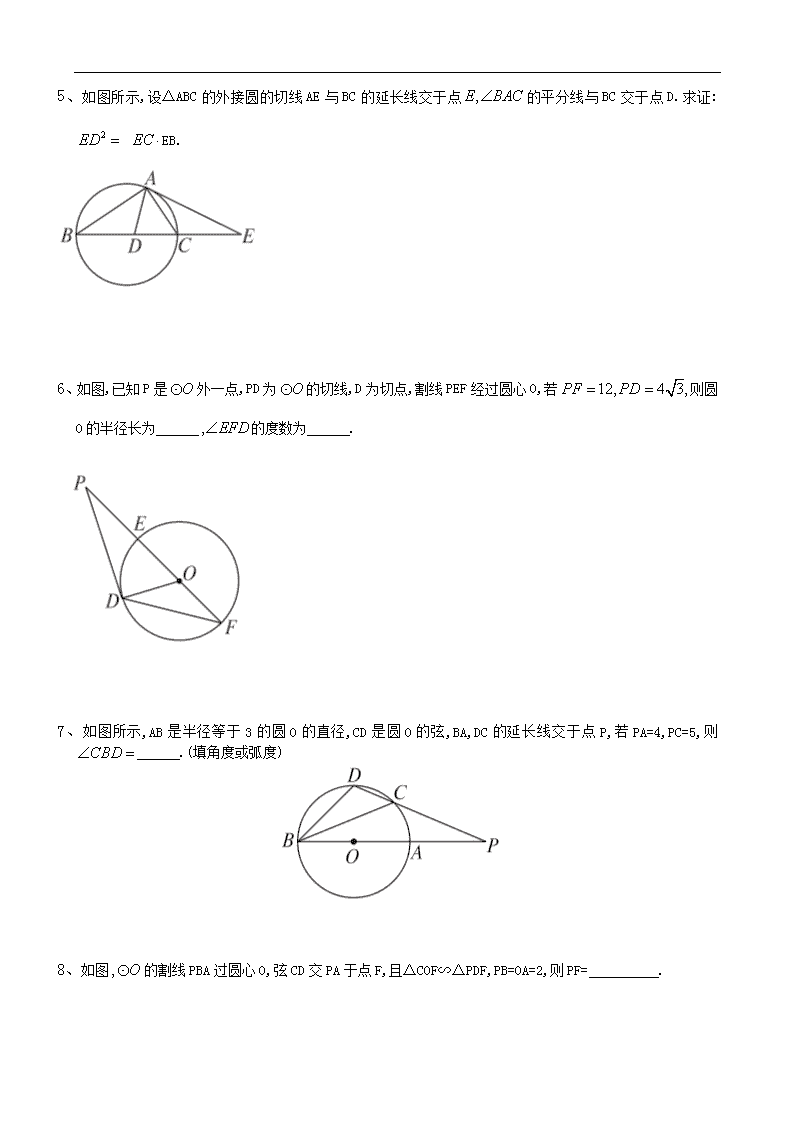
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013届高考数学一轮复习 直线与圆的位置关系
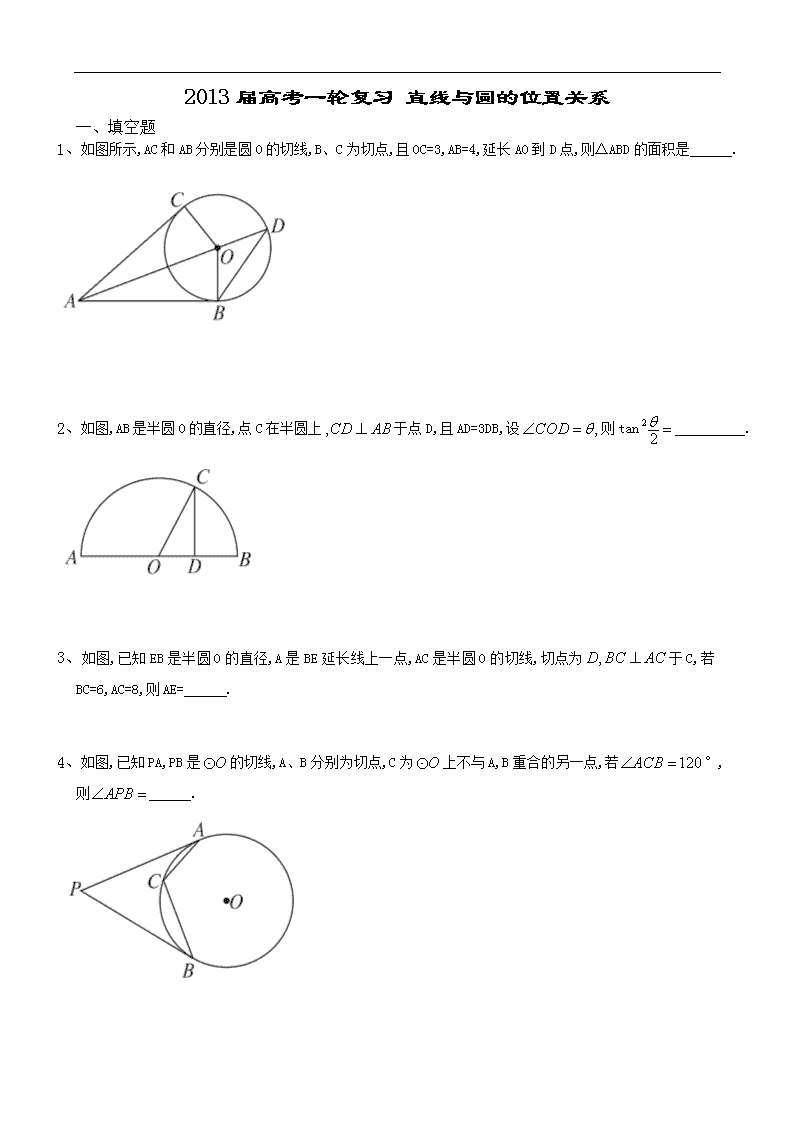
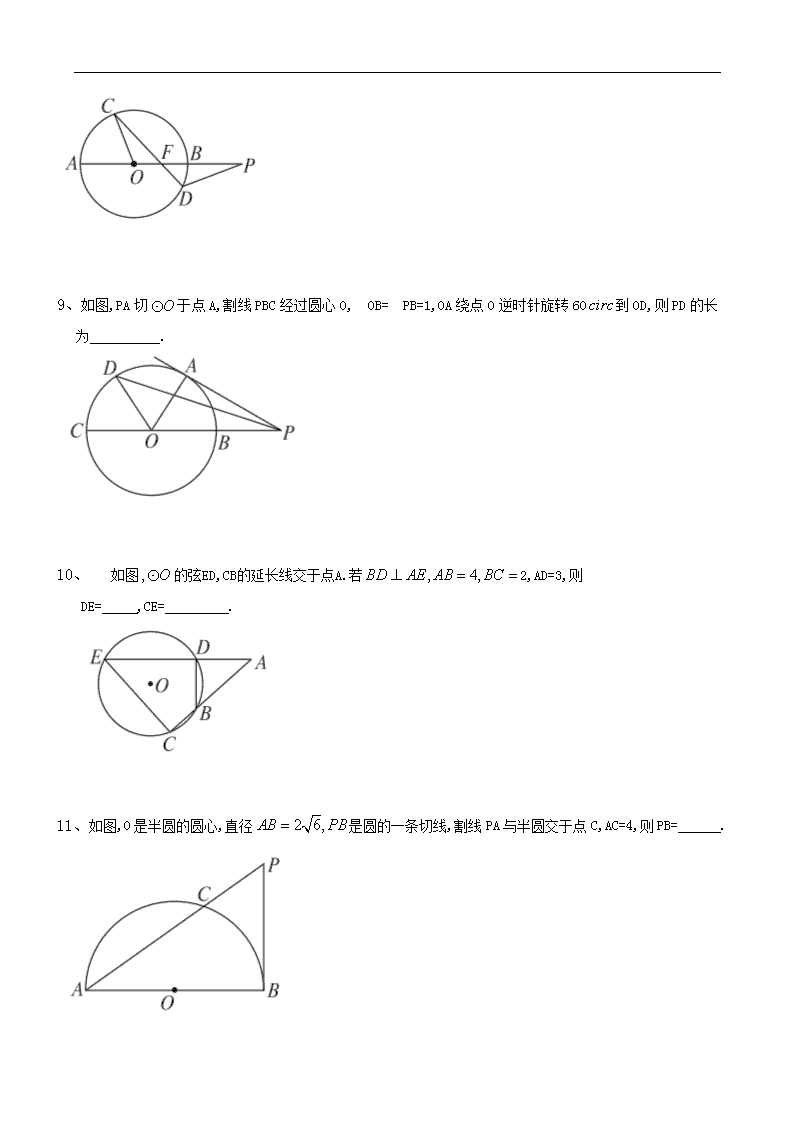
2013届高考一轮复习 直线与圆的位置关系 一、填空题 1、如图所示,AC和AB分别是圆O的切线,B、C为切点,且OC=3,AB=4,延长AO到D点,则△ABD的面积是 . 2、如图,AB是半圆O的直径,点C在半圆上于点D,且AD=3DB,设则tan . 3、如图,已知EB是半圆O的直径,A是BE延长线上一点,AC是半圆O的切线,切点为于C,若BC=6,AC=8,则AE= . 4、如图,已知PA,PB是的切线,A、B分别为切点,C为上不与A,B重合的另一点,若°,则 . 5、如图所示,设△ABC的外接圆的切线AE与BC的延长线交于点的平分线与BC交于点D.求证: EB. 6、如图,已知P是外一点,PD为的切线,D为切点,割线PEF经过圆心O,若则圆O的半径长为 的度数为 . 7、如图所示,AB是半径等于3的圆O的直径,CD是圆O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则 .(填角度或弧度) 8、如图的割线PBA过圆心O,弦CD交PA于点F,且△COF∽△PDF,PB=OA=2,则PF= . 9、如图,PA切于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60到OD,则PD的长为 . 10、 如图的弦ED,CB的延长线交于点A.若2,AD=3,则 DE= ,CE= . 11、如图,O是半圆的圆心,直径是圆的一条切线,割线PA与半圆交于点C,AC=4,则PB= . 12、如图,已知PA是的切线,A是切点,直线PO交于B、C两点,D是OC的中点,连接AD并延长交于点E.若°,则AE= . 13、如图,圆内的两条弦AB、CD相交于圆内一点P,已知PA则CD= . 二、解答题 14、从外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.求证:. 15、如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD. (1)求BD的长; (2)求的度数; (3)求的值. 16、如图的直径AB=4,C为圆周上一点,AC=2,过点C作的切线l,过点B作l的垂线BD,垂足为D,BD与交于点E. (1)求的度数; (2)求证:四边形OBEC是菱形. 以下是答案 一、填空题 1、 解析:由题知AB=AC. ∵∴AO=5. ∴sinsin=. 2、 解析:tantantan. 3、 解析:设圆的半径为R,连接 10-. 4、60° 解析:连接AO,BO,由°,得所对的弧为240°, ∴°,又°,得°. 5、证明:因为AE是圆的切线, 所以. 又因为AD是的平分线,所以. 从而. 因为 所以故EA=ED. 因为EA是圆的切线,所以由切割线定理知, 而EA=ED,所以. 6、4 30° 解析:连接DE,由切割线定理得. ∴EF=8,OD=4.∵ ∴°,∴°. 7、 30°(或 解析:由割线定理知:即10=5(DC+5),解得DC=3,所以△DOC是正三角形,所以°,而°. 8、3 解析:令OF=x,则即(x+2)(2-x)=x(2+2-x),x=1,所以PF=3. 9、 解析:∵PA切于点A,B为PO中点,∴AB=OB=OA,∴°,∴°,在△POD中由余弦定理,得:DOcos.∴. 10、5 解析:首先由割线定理不难知道于是AE=8,DE=5.又故BE为直径,因此°,由勾股定理可知故. 11、 解析:由射影定理得. 12、 解析:连接tan 30°,AO=2,PB=2,由余弦定理得cos 30° =7,所以.由相交弦定理得所以. 13、 解析:由相交弦定理可得 ∴9,即 ∴. 二、解答题 14、证明:∵PA为的切线, ∴ 而∴△PAC∽△PDA, 则.同理可得. ∵PA=PB,∴ ∴. 15、解:(1)连接OC,OB,AE,并延长BO交AE于点H, ∵AB是小圆的切线,C是切点, ∴ ∴C是AB的中点. ∵AD是大圆的直径, ∴O是AD的中点. ∴OC是△ABD的中位线. ∴BD=2OC=10. (2)由(1)知C是AB的中点. 同理F是BE的中点. 由切线长定理得BC=BF. ∴BA=BE. ∴. ∵ ∴°. (3)在Rt△OCB中, ∵OB=13,OC=5, ∴BC=12. 由(2)知. ∵ ∴△O∽△AGB. . 16、(1)解:在△AOC中,AC=2, ∵AO=OC=2, ∴△AOC是等边三角形. ∴°, ∴°. (2)证明:∵. ∴OC∥BD. ∴°. ∵AB为的直径, ∴△AEB为直角三角形°. ∴. ∴四边形OBEC为平行四边形. 又∵OB=OC=2. ∴四边形OBEC是菱形.查看更多