2020届二轮复习　算法初步学案（全国通用）

2020届二轮复习　算法初步学案（全国通用）

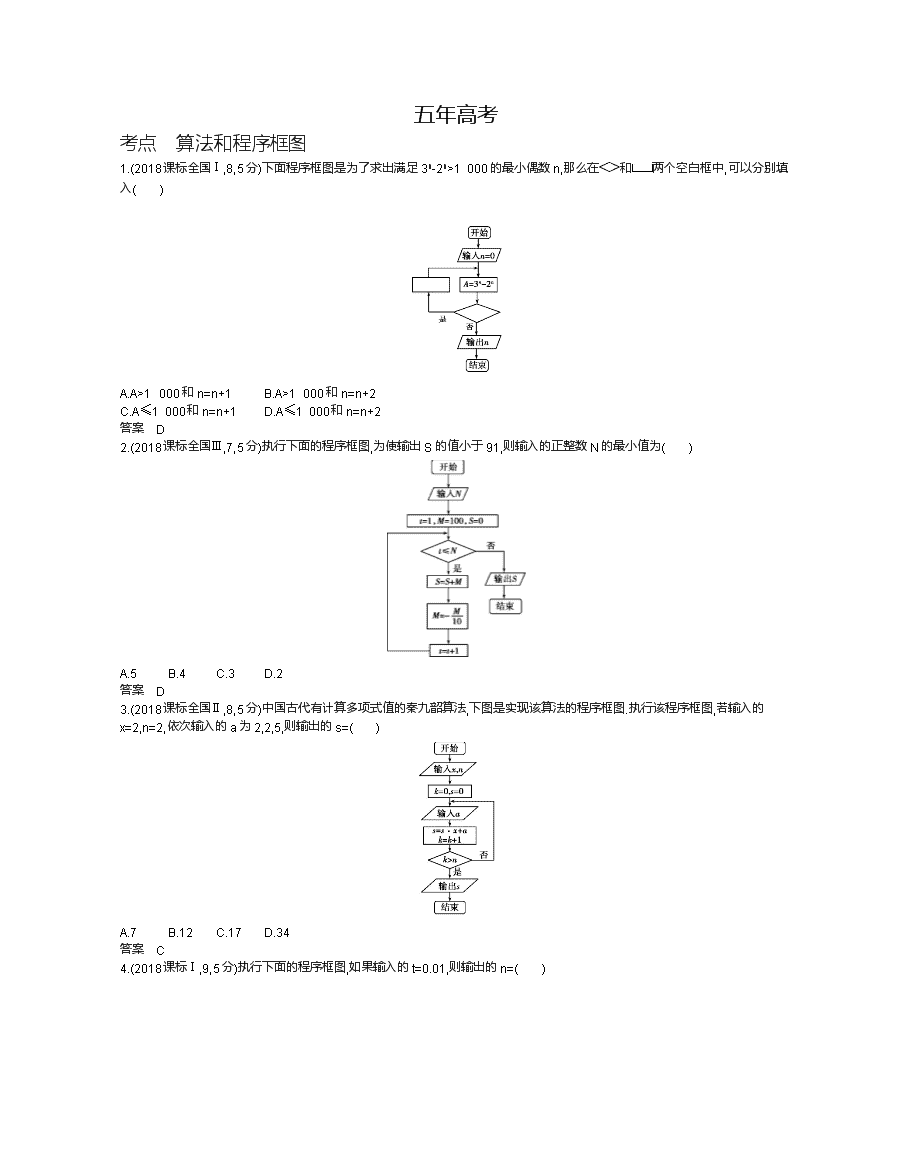
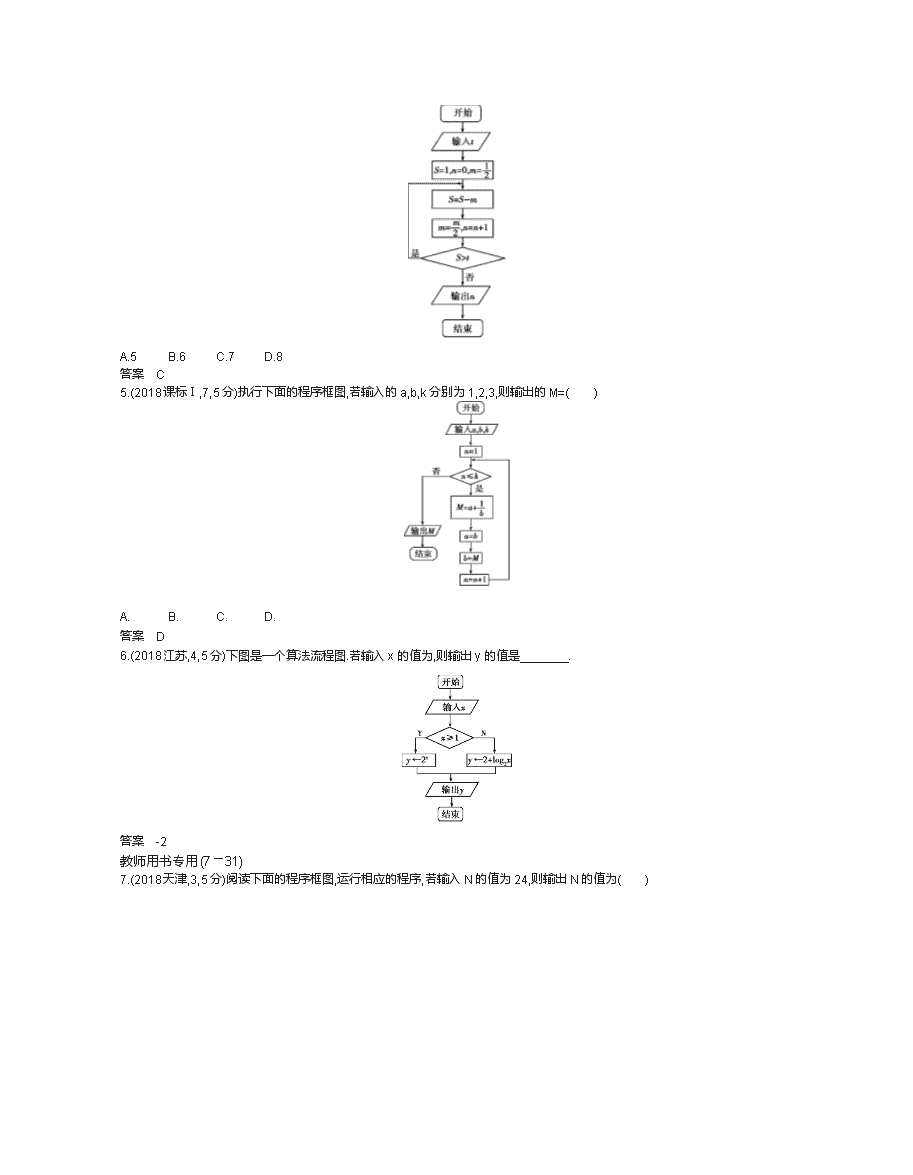
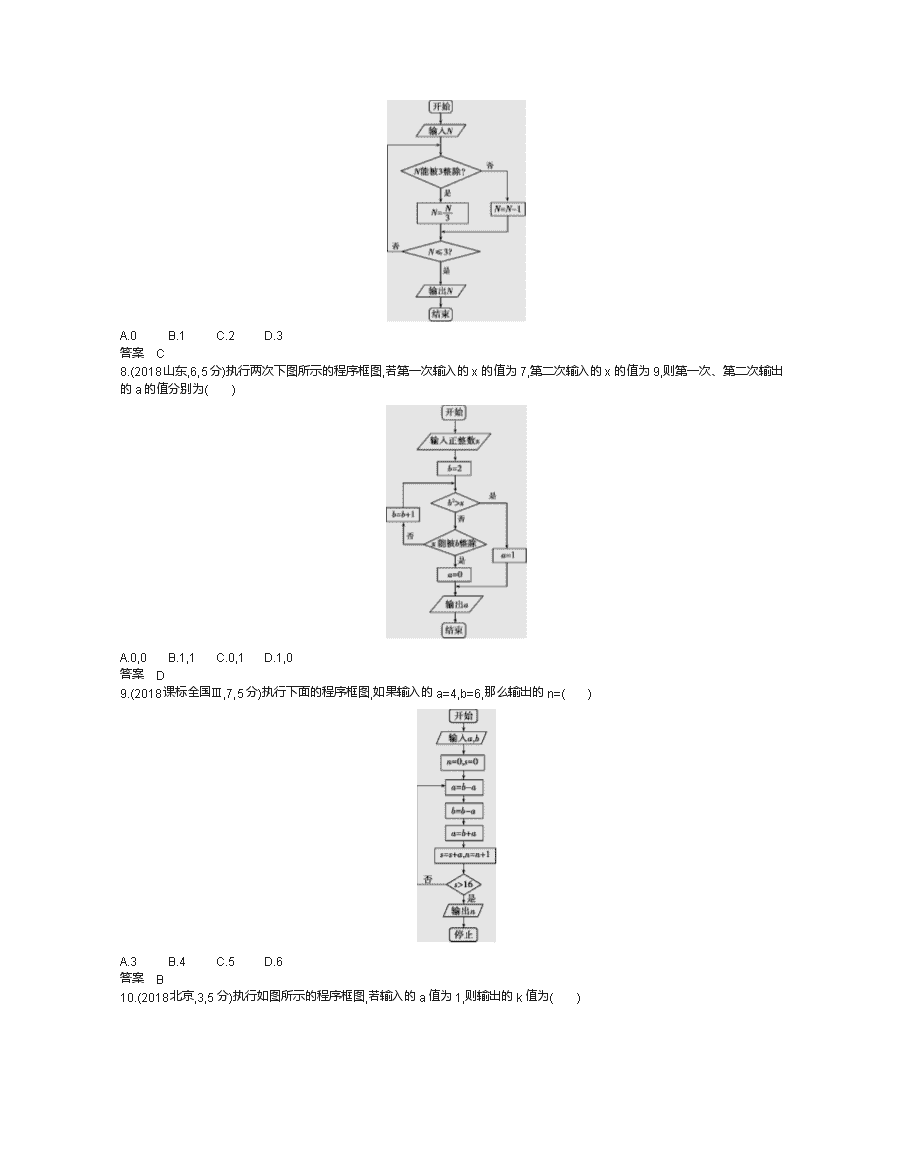
五年高考 考点　算法和程序框图 ‎1.(2018课标全国Ⅰ,8,5分)下面程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.A>1 000和n=n+1 B.A>1 000和n=n+2‎ C.A≤1 000和n=n+1 D.A≤1 000和n=n+2‎ 答案　D ‎2.(2018课标全国Ⅲ,7,5分)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为(　　)‎ A.5 B‎.4 ‎C.3 D.2‎ 答案　D ‎3.(2018课标全国Ⅱ,8,5分)中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=(　　)‎ A.7 B‎.12 ‎C.17 D.34‎ 答案　C ‎4.(2018课标Ⅰ,9,5分)执行下面的程序框图,如果输入的t=0.01,则输出的n=(　　)‎ A.5 B‎.6 ‎C.7 D.8‎ 答案　C ‎5.(2018课标Ⅰ,7,5分)执行下面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A. B. C. D.‎ 答案　D ‎6.(2018江苏,4,5分)下图是一个算法流程图.若输入x的值为,则输出y的值是　　　　. ‎ 答案　-2‎ 教师用书专用(7—31)‎ ‎7.(2018天津,3,5分)阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为(　　)‎ A.0 B‎.1 ‎C.2 D.3‎ 答案　C ‎8.(2018山东,6,5分)执行两次下图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为(　　)‎ A.0,0 B.1,‎1 ‎C.0,1 D.1,0‎ 答案　D ‎9.(2018课标全国Ⅲ,7,5分)执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=(　　)‎ A.3 B‎.4 ‎C.5 D.6‎ 答案　B ‎10.(2018北京,3,5分)执行如图所示的程序框图,若输入的a值为1,则输出的k值为(　　)‎ A.1 B‎.2 ‎C.3 D.4‎ 答案　B ‎11.(2018天津,4,5分)阅读下边的程序框图,运行相应的程序,则输出S的值为(　　)‎ A.2 B‎.4 ‎C.6 D.8‎ 答案　B ‎12.(2018四川,6,5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为(　　)‎ A.9 B‎.18 ‎C.20 D.35‎ 答案　B ‎13.(2018湖南,3,5分)执行如图所示的程序框图.如果输入n=3,则输出的S=(　　)‎ A. B. C. D.‎ 答案　B ‎14.(2018北京,3,5分)执行如图所示的程序框图,输出的结果为　(　　)‎ A.(-2,2) B.(-4,0) C.(-4,-4) D.(0,-8)‎ 答案　B ‎15.(2018课标Ⅱ,8,5分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=(　　)‎ A.0 B‎.2 ‎C.4 D.14‎ 答案　B ‎16.(2018陕西,8,5分)根据下边框图,当输入x为2 006时,输出的y=(　　)‎ A.28 B‎.10 ‎C.4 D.2‎ 答案　B ‎17.(2018福建,6,5分)阅读如图所示的程序框图,运行相应的程序,则输出的结果为(　　)‎ A.2 B‎.1 ‎C.0 D.-1‎ 答案　C ‎18.(2018北京,4,5分)当m=7,n=3时,执行如图所示的程序框图,输出的S值为(　　)‎ A.7 B‎.42 ‎C.210 D.840‎ 答案　C ‎19.(2018湖南,6,5分)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于(　　)‎ A.[-6,-2] B.[-5,-1] C.[-4,5] D.[-3,6]‎ 答案　D ‎20.(2018天津,3,5分)阅读下边的程序框图,运行相应的程序,输出S的值为(　　)‎ A.15 B‎.105 ‎C.245 D.945‎ 答案　B ‎21.(2018陕西,4,5分)根据下边框图,对大于2的整数N,输出的数列的通项公式是(　　)‎ A.an=2n B.an=2(n-1) ‎ C.an=2n D.an=2n-1‎ 答案　C ‎22.(2018重庆,5,5分)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是(　　)‎ A.s> B.s> C.s> D.s>‎ 答案　C ‎23.(2018江西,7,5分)阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为(　　)‎ A.7 B‎.9 ‎C.10 D.11‎ 答案　B ‎24.(2018课标全国Ⅰ,5,5分)执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于(　　)‎ A.[-3,4] B.[-5,2] ‎ C.[-4,3] D.[-2,5]‎ 答案　A ‎25.(2018课标全国Ⅱ,6,5分)执行下面的程序框图,如果输入的N=10,那么输出的S=(　　)‎ A.1+++…+ B.1+++…+‎ C.1+++…+ D.1+++…+‎ 答案　B ‎26.(2018山东,11,5分)执行如图所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为　　　　. ‎ 答案　3‎ ‎27.(2018江苏,4,5分)根据如图所示的伪代码,可知输出的结果S为　　　　. ‎ S←1‎ I←1‎ While　I<8‎ S←S+2‎ I←I+3‎ End　While Print　S 答案　7‎ ‎28.(2018山东,13,5分)执行下边的程序框图,输出的T的值为　　　　. ‎ 答案　‎ ‎29.(2018山东,11,5分)执行如图所示的程序框图,若输入的x的值为1,则输出的n的值为　　　　. ‎ 答案　3‎ ‎30.(2018湖北,13,5分)设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=　　. ‎ 答案　495‎ ‎31.(2018山东,13,4分)执行下面的程序框图,若输入的ε的值为0.25,则输出的n的值为　　　　. ‎ 答案　3‎ 三年模拟 A组　2018—2018年模拟·基础题组 考点　算法和程序框图 ‎1.(2018福建仙游金石中学期中,6)运行如图所示的程序框图,如果输入的t∈[-1,3],则输出的s属于(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.[-2,5] B.[-5,2] C.[-4,3] D.[-3,4]‎ 答案　D ‎2.(2018陕西宝鸡金台期中,8)执行如图所示的程序框图,如果输入的a=0.6,b=0.5,c=1.5,那么输出m的值是(　　)‎ A.0.5 ‎B.‎0.6 ‎C.1.5 D.都有可能 答案　A ‎3.(2018四川德阳三校联考,6)执行如图所示的程序框图,若输入m=1,n=3,输出x=1.75,则空白判断框内应填的条件为(　　)‎ A.|m-n|<1 B.|m-n|<0.5 ‎ C.|m-n|<0.2 D.|m-n|<0.1‎ 答案　B ‎4.(2018安徽黄山二模,6)已知x的取值范围是[0,8],执行如图所示的程序框图,则输出的y≥3的概率为(　　)‎ A. B. C. D.‎ 答案　B ‎5.(2018山西大学附属中学第二次模拟,5)阅读如图所示的程序框图,运行相应的程序,若输出的S为,则判断框中填写的内容可以是(　　)‎ A.n=6 B.n<‎6 ‎C.n≤6 D.n≤8‎ 答案　C ‎6.(人教A必3,一,1‎-1A,1,变式)已知图象不间断的函数f(x)是区间[a,b]上的单调函数,且在区间(a,b)上存在零点.如图是用二分法求方程f(x)=0近似解的程序框图,判断框内可以填写的内容有如下四个选择:‎ ‎①f(a)f(m)<0;②f(a)f(m)>0;③f(b)f(m)<0;④f(b)·f(m)>0.‎ 其中能够正确求出近似解的是(　　)‎ A.①④ B.②③ ‎ C.①③ D.②④‎ 答案　A B组　2018—2018年模拟·提升题组 ‎(满分:30分　时间:20分钟)‎ 选择题(每小题5分,共30分)‎ ‎1.(2018广东东莞二调,7)执行如图所示的程序框图,输出的结果为(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.7 B‎.9 ‎C.10 D.11‎ 答案　B ‎2.(2018广东茂名化州二模,7)公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n的值为(参考数据:sin 15°=0.258 8,sin 7.5°=0.130 5)(　　)‎ A.16 B‎.20 ‎C.24 D.48‎ 答案　C ‎3.(2018四省名校第一次联考,7)执行如图所示的程序框图,若输出的S的值为,则输入的n的值为(　　)‎ A.3 B‎.4 ‎C.5 D.6‎ 答案　B ‎4.(2018湖北荆州七校2月联考,8)宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=(　　)‎ A.2 B‎.3 ‎C.4 D.5‎ 答案　C ‎5.(2018广东韶关六校联考,10)阅读如图所示的程序框图,若输入a的值为,则输出k的值是(　　)‎ A.9 B‎.10 ‎C.11 D.12‎ 答案　B ‎6.(2018贵州遵义航天高中模拟,8)执行如图所示的程序框图,则输出的S的值为(　　)‎ A.1 B‎.2 ‎C.3 D.4‎ 答案　C C组　2018—2018年模拟·方法题组 方法1　基本逻辑结构和程序框图的运用 ‎1.(2018山东济宁3月模拟,8)执行如图所示的程序框图,则输出的S为(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.-2 B. C. D.3‎ 答案　D ‎2.(2018安徽江淮十校第一次联考,15)执行如图所示的程序框图,若p=0.8,则输出的n=　　　　. ‎ 答案　4‎ 方法2　程序框图的补充与完善 ‎3.(2018湖南长沙二模,7)我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值.这种算法至今仍是比较先进的算法.将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入(　　)‎ A.v=vx+a B.v=v(x+a) ‎ C.v=ax+v D.v=a(x+v)‎ 答案　A ‎4.(2018湖南三模,9)给出30个数:1,2,4,7,11,…,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么判断框①处和执行框②处应分别填入(　　)‎ A.i≤30?;p=p+i-1 ‎ B.i≤31?;p=p+i+1‎ C.i≤31?;p=p+i ‎ D.i≤30?;p=p+i 答案　D