数学文卷·2018届安徽省合肥市高三第一次教学质量检测（2018

数学文卷·2018届安徽省合肥市高三第一次教学质量检测（2018

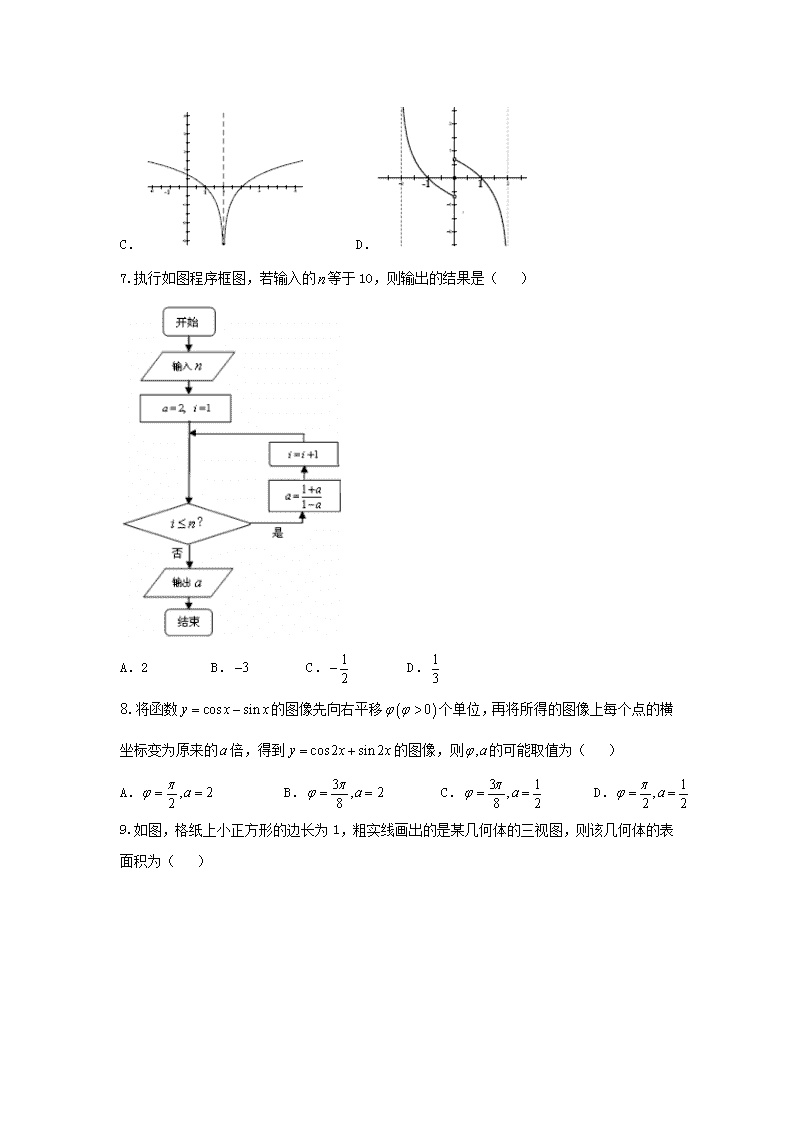
安徽省合肥市2018届高三第一次教学质量检测 数学文试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合，集合，则（ ）‎ A． B． C． D． ‎ ‎2.已知函数则（ ）‎ A． B．2 C．4 D．11‎ ‎3.已知为虚数单位，则（ ）‎ A．5 B． C． D．‎ ‎4.已知等差数，若，则的前7项的和等于（ ）‎ A．112 B．51 C．28 D．18‎ ‎5.某广播电台只在每小时的整点和半点开始播送新闻，时长均为5分钟，则一个人在不知道时间的情况下打开收音机收听该电台，能听到新闻的概率是（ ）‎ A． B． C． D． ‎ ‎6.函数的大致图像为（ ）‎ A． B．‎ C． D．‎ ‎7.执行如图程序框图，若输入的等于10，则输出的结果是（ ）‎ A．2 B． C． D． ‎ ‎8.将函数的图像先向右平移个单位，再将所得的图像上每个点的横坐标变为原来的倍，得到的图像，则的可能取值为（ ）‎ A． B． C． D．‎ ‎9.如图，格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）‎ A． B． C． D． ‎ ‎10. 已知数列的前项和为，若，则（ ）‎ A． B． C． D． ‎ ‎11.已知直线与曲线相切(其中为自然对数的底数)，则实数的值是（ ）‎ A． ‎ B． C．1 D．2 ‎ ‎12.如图，椭圆的焦点为，过的直线交椭圆于两点，交轴于点.若是线段的三等分点，则的周长为（ ）‎ A．20 B．10 C． D． ‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 若实数满足，则的最小值为 ．‎ ‎14.已知平面向量满足，，则在方向上的投影等于 ．‎ ‎15.若双曲线的一条渐近线被圆所截得的弦的长为2，则该双曲线的离心率等于 ．‎ ‎16.如图，已知平面四边形满足，将沿对角线翻折，使平面平面，则四面体外接球的体积为 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 在中，角所对的边分别为，.‎ ‎（1）求证：是等腰三角形；‎ ‎（2）若，且的周长为5，求的面积.‎ ‎18.一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在内的顾客中，随机抽取了180人，调查结果如表：‎ ‎（1）为推广移动支付，商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物，试根据上述数据估计，该商场当天应准备多少个环保购物袋？‎ ‎（2）某机构从被调查的使用移动支付的顾客中，按分层抽样的方式抽取7人作跟踪调查，并给其中2人赠送额外礼品，求获得额外礼品的2人年龄都在内的概率.‎ ‎19. 如图，在多面体中，是正方形，平面，平面，，点为棱的中点.‎ ‎（1）求证：平面平面；‎ ‎（2）若,求三棱锥的体积.‎ ‎20.已知抛物线上一点的纵坐标为4，且点到焦点的距离为5.‎ ‎（1）求抛物线的方程；‎ ‎（2）设斜率为的两条平行直线分别经过点和，如图.与抛物线交于两点，与抛 物线交两点.问：是否存在实数，使得四边形的面积为？若存在，求出的值；若不存在，请说明理由.‎ ‎21.已知函数.‎ ‎（1）求函数的单调区间；‎ ‎（2）当时，求证：. ‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系中，曲线 (为参数)，在以为极点，轴的正半轴为极轴的极坐标系中，曲线.‎ ‎（1）求曲线的普通方程；‎ ‎（2）若曲线上有一动点，曲线上有一动点，求的最小值.‎ ‎23.选修4-5：不等式选讲 已知函数.‎ ‎（1）解关于的不等式；‎ ‎（2）若关于的不等式的解集不是空集，求的取值范围.‎ 试卷答案 一、选择题 ‎1-5: BCACD 6-10: ACDCA 11、12：CD 二、填空题 ‎13. 1 14. 15. 16. ‎ 三、解答题 ‎17.（1）根据正弦定理，由可得 ‎ ‎ ‎，‎ 即，故，由得，‎ 故，所以是等腰三角形； ‎ ‎（2）由（1）知，.‎ 又因为的周长为，得.‎ 故的面积.‎ ‎（也可通过求出等腰三角形底边上的高计算面积）‎ ‎18.（1）由表可知，该商场使用移动支付的顾客的比例为，‎ 若当天该商场有12000人购物，则估计该商场要准备环保购物袋 个；‎ ‎（2）按年龄分层抽样时，抽样比例为，所以应从内抽取3人，从内抽取2人，从内抽取1人，从内抽取1人.‎ 记选出年龄在的3人为，其他4人为，7个人中选取2 人赠送额外礼品，有以下情况：‎ ‎，‎ ‎，‎ ‎， ‎ ‎，‎ ‎，‎ ‎.‎ 共有21种不同的情况，其中获得额外礼品的2人都在的情况有3种，‎ 所以，获得额外礼品的2人年龄都在内的概率为.‎ ‎19. （1）证明：设与交于点，则为的中点，‎ ‎∴.‎ ‎∵平面，平面，‎ ‎∴平面.‎ ‎∵平面，平面，且，‎ ‎∴，‎ ‎∴为平行四边形，∴.‎ ‎∵平面，平面，‎ ‎∴平面.‎ 又∵，‎ ‎∴平面平面.‎ ‎（2）连接.在正方形中，，‎ 又∵平面，∴.‎ ‎∵,‎ ‎∴平面，且垂足为， ‎ ‎∴,‎ ‎∴三棱锥的体积为.‎ ‎20.（1）由抛物线定义知，点到抛物线的准线的距离为5.‎ ‎∵抛物线的准线为，∴，‎ 解得，∴抛物线的方程为.‎ ‎（2）由已知得，直线.‎ 由 消去得， ‎ 这时，恒成立，.‎ 同理，直线，由 消去得， ‎ 由得，，‎ 又∵直线间的距离，‎ 则四边形的面积.‎ 解方程得，有唯一实数解2 (满足大于1)，‎ ‎∴满足条件的的值为.‎ ‎21.（1）的定义域为，.‎ 考虑.‎ ‎①当，即时，恒成立，在上单调递增；‎ ‎②当，即或时，由得.‎ 若，则恒成立，此时在上单调递增；‎ 若，则，‎ 此时或；‎ ‎ .‎ 综上，当时，函数的单调递增区间为，无单调递减区间，‎ 当时，的单调递增区间为，‎ 单调递减区间为.‎ ‎（2）当时，.‎ 令，‎ ‎.‎ 当时，；当时，， ‎ ‎∴在上单调递增，在上单调递减，即当时，取得最大值，‎ 故，即成立，得证.‎ ‎22. （1）由得：.‎ 因为，所以， ‎ 即曲线的普通方程为. ‎ ‎（2）由（1）可知，圆的圆心为，半径为1. ‎ 设曲线上的动点，‎ 由动点在圆上可得：.‎ ‎∵‎ ‎ 当时，，‎ ‎∴.‎ ‎23.（1），‎ 或或 或，‎ 所以，原不等式的解集为.‎ ‎（2）由条件知，不等式有解，则即可.‎ 由于，‎ 当且仅当，即当时等号成立，故.‎ 所以，的取值范围是.‎