第12章检测A卷-2020年领军高考数学一轮复习（文理通用） Word版含解析

第12章检测A卷-2020年领军高考数学一轮复习（文理通用） Word版含解析

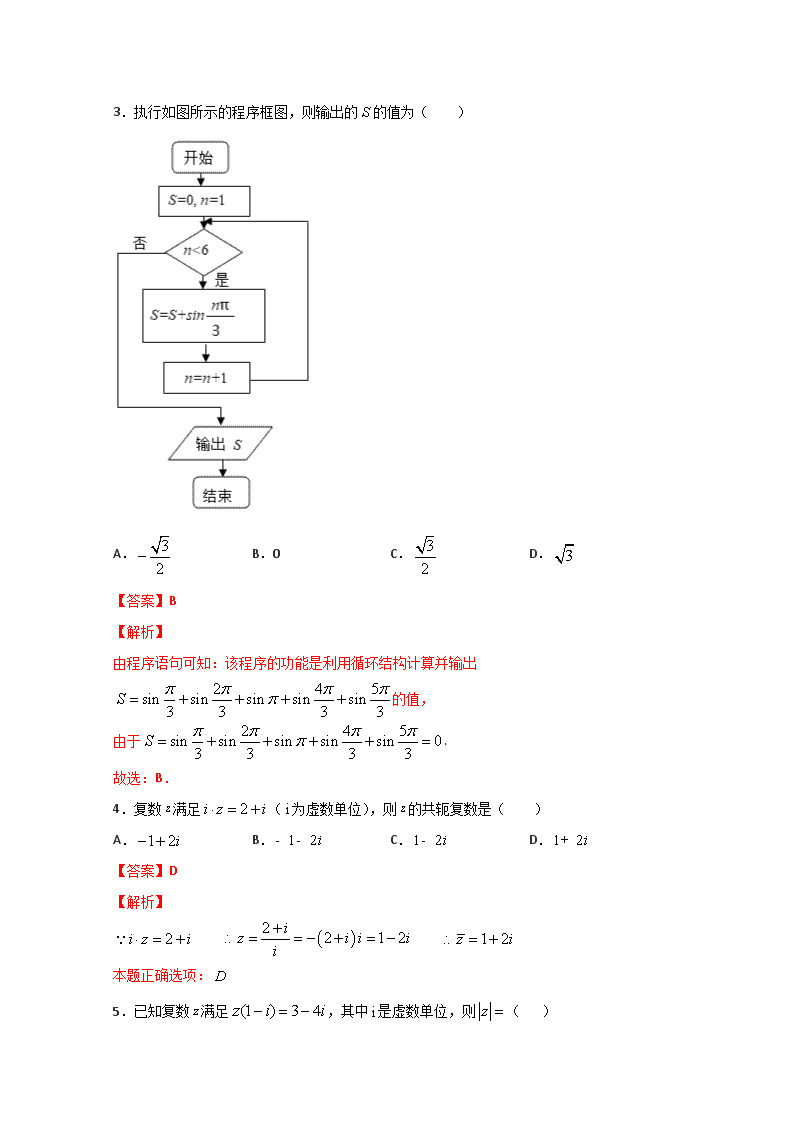
‎2020年领军高考数学一轮复习(文理通用)‎ 推理与证明、算法、复数 章节验收测试卷A卷 姓名 班级 准考证号 ‎ ‎ 1．i为虚数单位，则复数（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 直接由复数代数形式的除法运算化简复数，则答案可求．‎ ‎【详解】‎ ‎∵‎ ‎∴复数 故选：B ‎【点睛】‎ 本题考查了复数代数形式的除法运算，熟记运算性质，准确计算是关键，是基础题． 2．执行如图的程序框图，依次输入，则输出的值及其意义分别是（ ）‎ A．，即个数据的方差为 B．，即个数据的标准差为 C．，即个数据的方差为 D．，即个数据的标准差为 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据程序框图，输出的是这5个数据的方差，先求这5个数的均值，然后代入方差公式计算即可．‎ ‎【详解】‎ 根据程序框图，输出的S是这5个数据的方差，‎ ‎∵（17+19+20+21+23）＝20，‎ ‎∴由方差的公式得＝[（17﹣20）2+（19﹣20）2+（20﹣20）2+（21﹣20）2+（23﹣20）2]＝4．‎ 故选：A．‎ ‎【点睛】‎ 本题通过程序框图考查了均值和方差，解决问题的关键是通过程序框图能得出这是一个求数据方差的问题，属于基础题． ‎ ‎3．执行如图所示的程序框图，则输出的的值为（ ）‎ A． B．‎0 ‎C． D．‎ ‎【答案】B ‎【解析】‎ 由程序语句可知：该程序的功能是利用循环结构计算并输出的值，‎ 由于.‎ 故选：B． 4．复数满足（为虚数单位），则的共轭复数是（　　）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎ ‎ 本题正确选项： 5．已知复数满足，其中是虚数单位，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 由题意知：‎ 本题正确选项： 6．若复数满足，则复数在复平面对应的点位于（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【答案】D ‎【解析】‎ 解：，则复数在复平面对应的点为 位于第四象限.‎ 故选D. 7．《九章算术》卷第七——盈不足中有如下问题：“今有垣高九尺.瓜生其上，蔓日长七寸. 瓠生其下，蔓日长一尺.问几何日相逢.”翻译为“今有墙高9尺.瓜生在墙的上方，瓜蔓每天向下长7寸.葫芦生在墙的下方，葫芦蔓每天向上长1尺.问需要多少日两蔓相遇.”其中1尺=10寸.为了解决这一问题，设计程序框图如下所示，则输出的的值为（ ）‎ A．8 B．‎7 ‎C．6 D．5‎ ‎【答案】C ‎【解析】‎ 运行该程序，第一次，，；第二次，，；第三次，，；第四次，，；第五次，，；第六次，，此时输出的的值为6‎ 故选：C 8．如图所示的程序框图，运行相应的程序，则输出的值为（ ）‎ A．7 B．‎15 ‎C．31 D．63‎ ‎【答案】C ‎【解析】‎ 输入，‎ 第一次循环；‎ 第二次循环；‎ 第三次循环；‎ 第四次循环，‎ 退出循环，输出,故选C. 9．如图所示的程序框图，运行相应的程序，则输出的值为（ ）‎ A．3 B．‎2 ‎C． D．‎ ‎【答案】A ‎【解析】‎ 输入，‎ 第一次循环；‎ 第二次循环；‎ 第三次循环，‎ 退出循环输出，故选A. 10．已知，，则的共轭复数为 A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 由，得，‎ ‎∴，其共轭复数为，故选A． 11．复数（为虚数单位）是方程的根，则的值为（ ）‎ A． B．‎13 ‎C． D．5‎ ‎【答案】B ‎【解析】‎ ‎∵是方程z2﹣6z+b＝0（b∈R）的根，‎ 由实系数一元二次方程虚根成对原理可知，为方程另一根，‎ 则b＝（3+2i）（3﹣2i）＝13．‎ 故选：B． 12．如图的程序框图，当输出后，程序结束，则判断框内应该填（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 解析　当x＝－3时，y＝3；当x＝－2时，y＝0；‎ 当x＝－1时，y＝－1；当x＝0时，y＝0；‎ 当x＝1时，y＝3；当x＝2时，y＝8；‎ 当x＝3时，y＝15，x＝4，结束．‎ 所以y的最大值为15，可知x≤3符合题意．‎ 判断框应填：‎ 故选 13．秦九韶是我国南宋时期的数学家，他在所著《数书九章》中提出的求多项式值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图，是利用秦九韶算法求一个多项式的值，若输入n、x的值分别为3、 ，则输出v的值为______‎ ‎【答案】‎ ‎【解析】‎ ‎ 模拟程序：‎ 的初始值分别为 第1次循环：，，不满足；‎ 第2次循环：，，不满足； ‎ 第3次循环：，，满足；‎ 故输出. 14．我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与古希腊的算法—“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”，当输入时，输出的_____.‎ ‎【答案】3‎ ‎【解析】‎ 解法一：按照程序框图运行程序，输入：，‎ 则，，，不满足，循环；‎ 则，，，不满足，循环；‎ 则，，，不满足，循环；‎ 则，，，满足，输出 解法二：程序框图的功能为“辗转相除法”求解两个正整数的最大公约数 因为与的最大公约数为 ‎ 本题正确结果： 15．执行如图所示的程序框图，输出的为_________.‎ ‎【答案】1‎ ‎【解析】‎ 执行程序框图，输入，‎ 第一次循环；‎ 第二次循环； ‎ 第三次循环；‎ 第四次循环；‎ 第五次循环；‎ 第六次循环；‎ 第七次循环；‎ 第八次循环；‎ 第九次循环；‎ 第十次循环；‎ 退出循环输出，故答案为1. 16．将正奇数按如图所示的规律排列：‎ ‎1‎ ‎3 5 7‎ ‎9 11 13 15 17‎ ‎19 21 23 25 27 29 31‎ ‎………………‎ 则2019在第_____行，从左向右第______个数 ‎【答案】32. 49. ‎ ‎【解析】‎ 根据排列规律可知，第一行有1个奇数，第2行有3个奇数，第3行有5个奇数……‎ 可得第n行有个奇数，‎ 前n行总共有个奇数.‎ 当时，共有个奇数，当时，共有个奇数.‎ 所以2019是第1010个奇数，在第32行第49个数. ‎ ‎17．已知数列，，，，，，记数列的前项和．‎ ‎1计算，，，；‎ ‎2猜想的表达式，并用数学归纳法证明．‎ ‎【答案】1 ，，，；2 ，证明见解析.‎ ‎【解析】‎ ‎ ；；；；‎ 猜想．‎ 证明：当时，结论显然成立；‎ 假设当时，结论成立，即，‎ 则当时，，‎ 当时，结论也成立，‎ 综上可知，对任意，．‎ 由，知，等式对任意正整数都成立． 18．（1）设，，都是正数，求证：；‎ ‎（2）证明：求证.‎ ‎【答案】（1）证明见解析；（2）证明见解析.‎ ‎【解析】‎ ‎（1）由题意，因为 ‎，‎ 所以，当且仅当时，等号成立.‎ ‎（2）证明：要证，‎ 只需证明，‎ 即证明，‎ 也就是证明，‎ 上式显然成立，故原不等式成立. 19．已知，其前项和为.‎ ‎（1）计算；‎ ‎（2）猜想的表达式，并用数学归纳法进行证明.‎ ‎【答案】（1）；（2），证明见解析.‎ ‎【解析】‎ ‎（1）计算，.‎ ‎（2）猜想.‎ 证明：①当时，左边，右边，猜想成立.‎ ‎②假设猜想成立，即成立，‎ 那么当时，，‎ 而，故当时，猜想也成立.‎ 由①②可知，对于，猜想都成立. 20．如图（A），（B），（C），（D）为四个平面图形:‎ ‎（A）（B）（C）（D）‎ ‎（I）数出每个平面图形的交点数、边数、区域数，并将列联表补充完整；‎ 交点数 边数 区域数 ‎（A）‎ ‎4‎ ‎5‎ ‎2‎ ‎（B）‎ ‎5‎ ‎8‎ ‎（C）‎ ‎12‎ ‎5‎ ‎（D）‎ ‎15‎ ‎（II）观察表格，若记一个平面图形的交点数、边数、区域数分别为，试猜想间的数量关系（不要求证明）.‎ ‎【答案】（I）列联表见解析；（II）.‎ ‎【解析】‎ ‎（I）‎ ‎（II）观察表格，若记一个平面图形的交点数、边数、区域数分别为，猜想之间的数量关系为. 21．函数令，．‎ ‎（1）求并猜想的表达式（不需要证明）； ‎ ‎（2）与相切，求的值．‎ ‎【答案】（1）见解析；（2）4‎ ‎【解析】‎ ‎（1）， ‎ ‎.‎ 猜想 .‎ ‎（2）设切点为，‎ ‎，, ‎ 切线斜率， ‎ 解得. ‎ 所以.‎ 所以，解得. 22．已知函数对任意实数都有，且.‎ ‎（I）求的值，并猜想的表达式；‎ ‎（II）用数学归纳法证明（I）中的猜想.‎ ‎【答案】（I）；（II）证明见解析.‎ ‎【解析】‎ ‎（I），‎ ‎，‎ ‎，‎ ‎，‎ 猜想.‎ ‎（II）证明：当时，，猜想成立；‎ 假设时，猜想成立，即，‎ 则当时，，‎ 即当时猜想成立.‎ 综上，对于一切均成立.‎