【数学】安徽省定远县民族中学2020届高三5月模拟检测（文）

【数学】安徽省定远县民族中学2020届高三5月模拟检测（文）

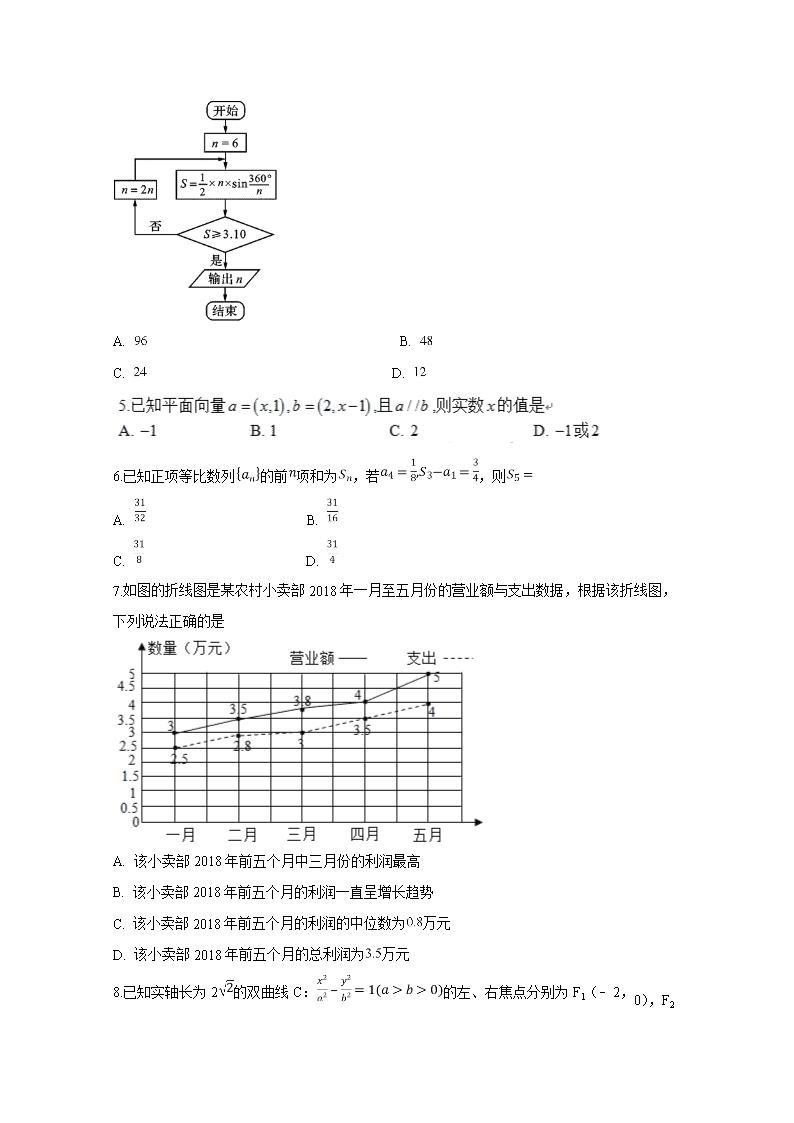
安徽省定远县民族中学2020届高三5月模拟检测（文）‎ 全卷满分150分，考试用时150分钟。‎ 注意事项：‎ ‎1、答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2、作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。‎ ‎3、考试结束后，将本试卷和答题卡一并收回。‎ 第I卷 选择题（共60分）‎ 一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。) ‎ ‎1.设集合， ， ，则的取值范围为 A. 或 B. ‎ C. D. 或 ‎2.已知复数（其中为虚数单位），则的值为 A. 1 B. C. 2 D. ‎ ‎3.已知函数， 的图像与的图像关于轴对称，函数，若关于的不等式恒成立，则实数的取值范围为 A. B. ‎ C. D. ‎ ‎4.公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n值为 (参考数据：，，)‎ A. B. ‎ C. D. ‎ ‎6.已知正项等比数列的前项和为，若，则 A. B. ‎ C. D. ‎ ‎7.如图的折线图是某农村小卖部2018年一月至五月份的营业额与支出数据，根据该折线图，下列说法正确的是 A. 该小卖部2018年前五个月中三月份的利润最高 B. 该小卖部2018年前五个月的利润一直呈增长趋势 C. 该小卖部2018年前五个月的利润的中位数为万元 D. 该小卖部2018年前五个月的总利润为万元 ‎8.已知实轴长为2的双曲线C：的左、右焦点分别为F1（﹣2，0），F2‎ ‎（2，0），点B为双曲线C虚轴上的一个端点，则△BF1F2的重心到双曲线C的渐近线的距离为 A. B. C. D. ‎ ‎9.函数在区间上的图象大致为 A. B. ‎ C. D. ‎ ‎10.将函数的图象向右平移个单位长度，得到函数的图象，则在上的最小值为 A. B. ‎ C. D. 0‎ ‎11.已知是函数的零点，是函数的零点，且满足，则实数的最小值是 A. B. ‎ C. -2 D. -1‎ ‎12.如图，四棱锥的底面为矩形，矩形的四个顶点，，，在球的同一个大圆上，且球的表面积为，点在球面上，则四棱锥体积的最大值为 A. 8 B. ‎ C. 16 D. ‎ 第II卷 非选择题（共90分）‎ 本卷包括必考题和选考题两部分。第13题-第21题为必考题，每个试题考生都必须作答。第22题-第23题为选考题，考生根据要求作答。‎ 二、填空题(本大题共4小题,每小题5分,共20分) ‎ ‎13.设实数满足，则的取值范围为_________.‎ ‎14.已知双曲线 的左、右焦点分别为 、 ，上存在一点满足，且到坐标原点的距离等于双曲线的虚轴长，则双曲线的渐近线方程为__________．‎ ‎15.已知直线与圆相交于两点，点分别在圆上运动，且位于直线两侧，则四边形面积的最大值为______．‎ ‎16.下列命题正确的是__________．（写出所有正确命题的序号）‎ ‎①已知，“且”是“”的充要条件；‎ ‎③已知，“”是“”的充分不必要条件；‎ ‎④命题：“，使且”的否定为：“，都有且”‎ 三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。)‎ ‎17. （本小题满分12分）‎ 已知中，角所对的边分别为，且， .‎ ‎（1）若，求的大小；‎ ‎（2）若为三个连续正整数，求的面积.‎ ‎18. （本小题满分12分） ‎ 艾滋病是一种危害性极大的传染病，由感染艾滋病病毒病毒引起，它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标，使人体丧失免疫功能下表是近八年来我国艾滋病病毒感染人数统计表：‎ 年份 ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ 年份代码x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 感染者人数单位：万人 ‎85‎ 请根据该统计表，画出这八年我国艾滋病病毒感染人数的折线图；‎ 请用相关系数说明：能用线性回归模型拟合y与x的关系；‎ 建立y关于x的回归方程系数精确到，预测2019年我国艾滋病病毒感染人数．‎ 参考数据：；，，，‎ 参考公式：相关系数，‎ 回归方程中， ，．‎ ‎19. （本小题满分12分）‎ 已知数列满足，，设，.‎ ‎（1）判断数列是否为等比数列，说明理由并求的通项公式；‎ ‎（2）求数列的前项和.‎ ‎20. （本小题满分12分）‎ 已知点是抛物线的焦点，点是抛物线上一点，且，的方程为，过点作直线，与抛物线和依次交于.（如图所示）‎ ‎（1）求抛物线的方程；‎ ‎（2）求的最小值.‎ ‎21. （本小题满分12分）‎ 已知函数，．‎ ‎（1）若是的极值点， 求并讨论的单调性；‎ ‎（2）若时，，求的取值范围．‎ ‎22. （本小题满分10分）选修4—4：坐标系与参数方程 在平面直角坐标系中，曲线的参数方程是为参数)，直线的参数方程是（为参数）．‎ ‎（1）分别求曲线、直线的普通方程；‎ ‎（2）直线与交于两点，则求的值.‎ ‎23. （本小题满分10分）选修4-5：不等式选讲 定义在上的函数，若，有，则称函数为定义在上的非严格单增函数；若，有，则称函数为定义在上的非严格单减函数.已知： .‎ ‎（1）若函数为定义在上的非严格单增函数，求实数的取值范围.‎ ‎（2）若函数为定义在上的非严格单减函数，试解不等式.‎ 参考答案 ‎1-10.BDCC DBDABA 11.D 12.D ‎ ‎13. 14. 15. 16.③‎ ‎17.（1）（2）的面积为 解析：（1）∵，∴由正弦定理有，‎ 又，即，于是，‎ 在中， ，于是， .‎ ‎（2）因为，故，故设， ， ， ；‎ 由，得，‎ ‎∴.‎ 由余弦定理得： ，代入可得：‎ ‎，解得： ，∴， ， ，‎ 故，故，‎ 故的面积为.‎ ‎18.解：（1）我国艾滋病病毒感染人数的折线图如图所示 ‎，，‎ ‎，‎ ‎．‎ 故具有强线性相关关系．‎ ‎，，‎ ‎．‎ 当时，．‎ 故预测2019年我国艾滋病感染累积人数为万人．‎ ‎19.解：（1）{bn}是首项为1，公比为2的等比数列.由条件可得，即bn+1=2bn，‎ 又b1=1，所以，所以，所以{bn}是首项为1，公比为2的等比数列.‎ 所以，即，所以.‎ ‎（2）由（1）可，所以，‎ 所以，‎ 所以数列的前项和.‎ ‎20.（1）；（2）． ‎ 解析由在抛物线上得，‎ 又由得，‎ 解得，，又，故.‎ 所以抛物线的方程为.………………4分 由题知直线的斜率一定存在，设直线的方程为.‎ 则圆心到直线的距离为，‎ ‎.………………6分 设，，‎ 由得，‎ 则，由抛物线定义知，………………8分 ‎.………………10分 设，‎ 则，，‎ 函数在上都是单调递增函数， ‎ 当时即时，有最小值.………………12分 ‎21.（1），.‎ 因为是的极值点，‎ 所以，可得．‎ 所以，.‎ 因为在上单调递增，且时，，‎ 所以时，，，单调递减；‎ 时， ，，单调递增．‎ 故在上单调递减，在上单调递增．‎ ‎（2）由得，‎ 因为，所以.‎ 设，‎ 则.‎ 令，‎ 则，‎ 显然在内单调递减，且，‎ 所以时，，单调递减， 则，即，‎ 所以在内单减，从而.‎ 所以.‎ ‎22.（1）；（2）.‎ 解析：（1）：； ：‎ ‎（2）直线的标准参数方程为，（为参数）‎ 将的标准参数方程代入的直角坐标方程得：，所以，‎ ‎23.（1）；（2）当时，不等式的解集为：∅；当时，不等式的解集为： .‎ 解析：（1）当时， ；‎ 当时， ；‎ 当时， .‎ 因为为定义在上的非严格单增函数，根据定义，可得： .‎ ‎（2）函数为定义在上的非严格单减函数，由（1）知，且.‎ 所以，当时， 不等式的解集为：∅；‎ 当时，不等式,即 或 或 解得 或 即所以的解集为： .‎