- 2021-06-11 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:三角函数图像的变换
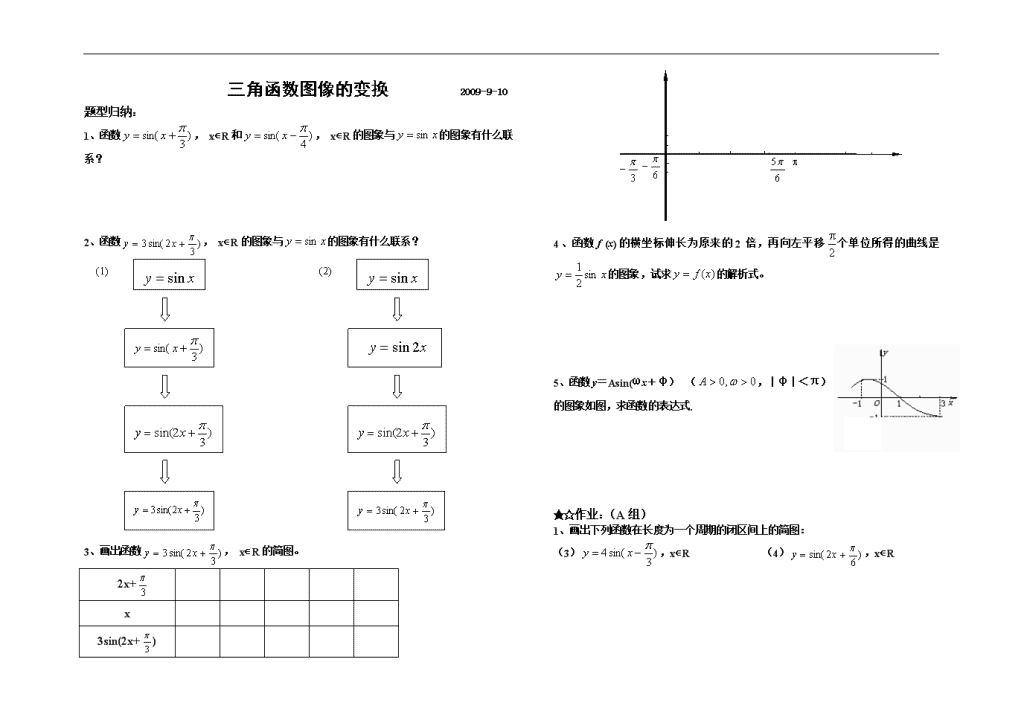
三角函数图像的变换 2009-9-10 题型归纳: 1、函数, xÎR和, xÎR的图象与的图象有什么联系? 2、函数, xÎR的图象与的图象有什么联系? (2) (1) 2 y 3、画出函数, xÎR的简图。 2x+ x 3sin(2x+) 1 y p 4p 3p p O x -1 4、函数f (x)的横坐标伸长为原来的2倍,再向左平移个单位所得的曲线是的图象,试求的解析式。 5、函数y=Asin(ωx+φ)(,|φ|<π)的图象如图,求函数的表达式. ★☆作业:(A组) 1、画出下列函数在长度为一个周期的闭区间上的简图: (3),xÎR (4),xÎR 2、说明下列函数的图像由正弦函数或余弦函数经过了怎样的变换。 (1),xÎR (2),xÎR (3),xÎR (4),xÎR 3、不画简图,直接 写出下列函数的振幅、周期和初相,并说明这些 函数的图象可由正弦曲线经过怎样的变化得出(注意定义域): (1),xÎ[0,+∞) (2),xÎ[0,+∞) 4、(1)y=sin(x+)是由y=sinx向 平移 个单位得到的. (2)y=sin(x-)是由y=sinx向 平移 个单位得到的. (3)y=sin(x-)是由y=sin(x+)向 平移 个单位得到的. 5、若将某函数的图象向右平移以后所得到的图象的函数式是y=sin(x+),则原来的函数表达式为( ) A.y=sin(x+) B.y=sin(x+) C.y=sin(x-) D.y=sin(x+)- 6、把函数y=cos(3x+)的图象适当变动就可以得到y=sin(-3x)的图象,这种变动可以是( ) A.向右平移 B.向左平移 C.向右平移 D.向左平移 ★★☆☆作业( B组): 7、如图:是函数y=Asin(ωx+φ)+2的图象的一部分,它的振幅、周期、初相各是 ( ) A.A=3,T=,φ=- B.A=1,T=,φ=- C.A=1,T=,φ=- D.A=1,T=,φ=- 8、如左下图是函数y=Asin(ωx+φ)的图象的一段,它的解析式为 ( ) A.B. C. D. 9、如右上图所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)|φ|<的图象的一部分,求这个函数的解析式。 10、设函数y = sin(x - )cosx; ①求出函数的单调区间;②求出函数的值域。查看更多