四川省内江市2019-2020学年高二上学期期末检测 数学（文）

四川省内江市2019-2020学年高二上学期期末检测 数学（文）

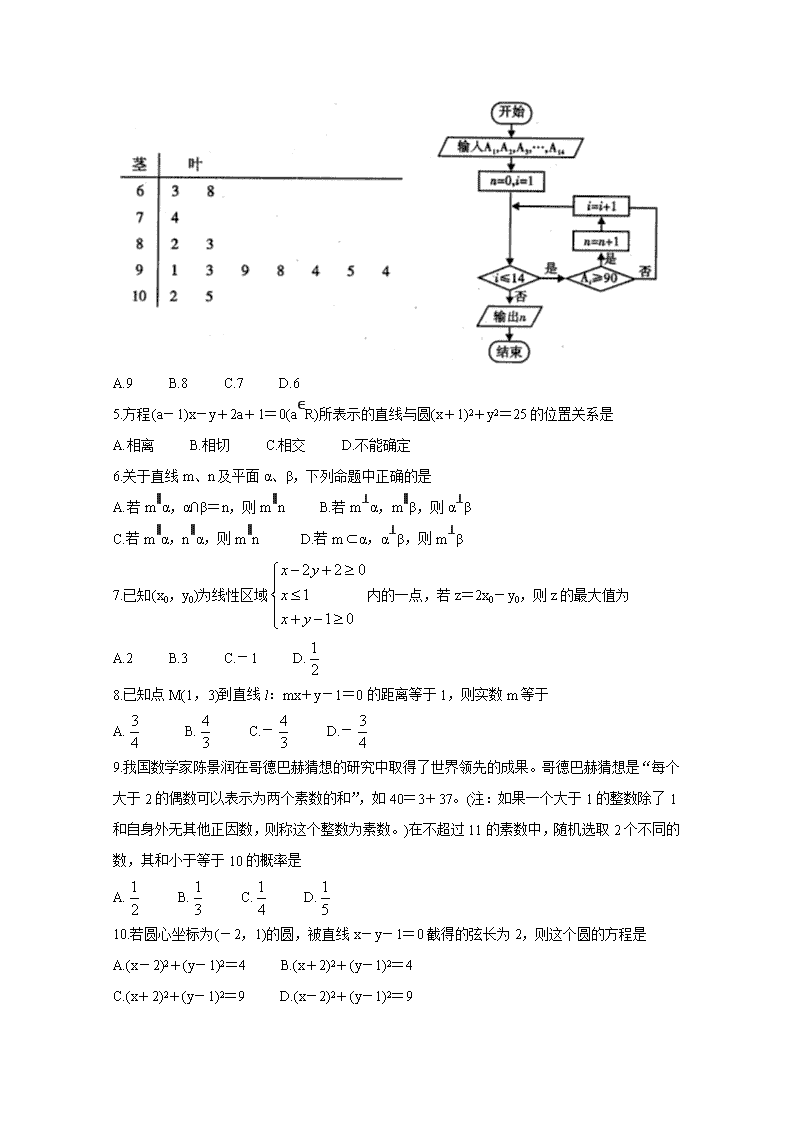
内江市2019－2000学年度第一学期高二期末检测题 数学(文科)‎ 本试卷共4页，全卷满分150分，考试时间120分钟。‎ 注意事项：‎ ‎1.答题前，考生务必将自己的姓名、考号、班级用签字笔填写在答题卡相应位置。‎ ‎2.选择题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案。不能答在试题卷上。‎ ‎3.非选择题用签字笔将答案直接答在答题卡相应位置上。‎ ‎4.考试结束后，监考人员将答题卡收回。‎ 一、选择题：(本大题共12个小题，每小题5分，共60分。在每小题的四个选项中只有一个是正确的，把正确选项的代号填涂在答题卡的指定位置上。)‎ ‎1.已知某班有学生48人，为了解该班学生视力情况，现将所有学生随机编号，用系统抽样的方法抽取一个容量为4的样本，已知3号，15号，39号学生在样本中，则样本中另外一个学生的编号是 A.26 B.27 C.28 D.29‎ ‎2.设B点是点A(2，－3，5)关于平面xOy的对称点，则|AB|＝‎ A. B.38 C. D.10‎ ‎3.直线l1、l2的斜率是方程x2＋2x－1＝0的两根，则l1与l2的位置关系是 A.平行 B.垂直 C.相交但不垂直 D.重合 ‎4.如图是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A1，A2，A3，…，A14，下图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图，那么输出的结果是 A.9 B.8 C.7 D.6‎ ‎5.方程(a－1)x－y＋2a＋1＝0(a∈R)所表示的直线与圆(x＋1)2＋y2＝25的位置关系是 A.相离 B.相切 C.相交 D.不能确定 ‎6.关于直线m、n及平面α、β，下列命题中正确的是 A.若m∥α，α∩β＝n，则m∥n B.若m⊥α，m∥β，则α⊥β C.若m∥α，n∥α，则m∥n D.若mα，α⊥β，则m⊥β ‎7.已知(x0，y0)为线性区域内的一点，若z＝2x0－y0，则z的最大值为 A.2 B.3 C.－1 D. ‎ ‎8.已知点M(1，3)到直线l：mx＋y－1＝0的距离等于1，则实数m等于 A. B. C.－ D.－‎ ‎9.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如40＝3＋37。(注：如果一个大于1的整数除了1和自身外无其他正因数，则称这个整数为素数。)在不超过11的素数中，随机选取2个不同的数，其和小于等于10的概率是 A. B. C. D.‎ ‎10.若圆心坐标为(－2，1)的圆，被直线x－y－1＝0截得的弦长为2，则这个圆的方程是 A.(x－2)2＋(y－1)2＝4 B.(x＋2)2＋(y－1)2＝4‎ C.(x＋2)2＋(y－1)2＝9 D.(x－2)2＋(y－1)2＝9‎ ‎11.若圆C：(x－3)2＋(y－4)2＝1上存在点P，使得，其中点M(－t，0)、N(t，0)(t∈R＋)，则t的最小值是 A.7 B.5 C.4 D.6‎ ‎12.已知正三棱锥A－BCD的外接球是球O，正三棱锥底边BC＝3，侧棱AB＝2，点E在线段BD上，且BE＝DE，过点E作球O的截面，则所得截面圆面积的取值范围是 A.[，3π] B.[2π，3π] C.[，4π] D.[，4π]‎ 二、填空题：(本大题共4小题，每小题5分，共20分。)‎ ‎13.已知x1，x2，x3，…，xn的平均数为a，则2x1＋3，2x2＋3，…，2xn ＋3的平均数是 。‎ ‎14.秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法。已知一个5次多项式f(x)＝4x5－3x3－2x2－5x＋1，用秦九韶算法求这个多项式当x＝3时的值为 。‎ ‎15.一条光线从点(2，－3)射出，经x轴反射，其反射光线所在直线与圆(x－3)2＋y2＝1相切，则反射光线所在的直线方程为 。‎ ‎16.如图所示，在长方体ABCD－A1B1C1D1中，点E是棱CC1上的一个动点，若平面BED1交棱AA1于点F，给出下列命题：‎ ‎①四棱锥B1－BED1F的体积恒为定值；‎ ‎②对于棱CC1上任意一点E，在棱AD上均有相应的点G，使得CG//平面EBD1；‎ ‎③O为底面ABCD对角线AC和BD的交点，在棱DD1上存在点H，使OH//平面EBD1；‎ ‎④存在唯一的点E，使得截面四边形BED1F的周长取得最小值。其中为真命题的是 。(填写所有正确答案的序号)‎ 三、解答题：(本大题共6个小题，共70分。解答要写出文字说明，证明过程或演算步骤。)‎ ‎17.(本小题满分10分)‎ 已知△ABC的三个顶点坐标分别为A(－2，－4)、B(2，4)、C(5，－1)。‎ ‎(1)求边AB上的中线所在直线的一般式方程；‎ ‎(2)求边AB上的高所在直线的一般式方程。‎ ‎18.(本小题满分12分)‎ 某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60)，[60，70)，[70，80)，[80，90)，[90，100]。‎ ‎ ‎ ‎(1)求图中a的值；‎ ‎(2)根据频率分布直方图，估计这100名学生语文成绩的平均数与中位数。‎ ‎19.(本小题满分12分)‎ 如图，把长为6，宽为3的矩形折成正三棱柱ABC－A1B1C1，三棱柱的高度为3，矩形的对角线和三棱柱的侧棱BB1、CC1的交点记为E、F。‎ ‎ ‎ ‎(1)在三棱柱ABC－A1B1C1中，若过A1、E、F三点做一平面，求截得的几何体A1B1C1EF的表面积；‎ ‎(2)求三棱锥A1－AEF的体积。‎ ‎20.(本小题满分12分)‎ 某公交公司为了方便市民出行，科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为了研究车辆发车间隔时间x与乘客等候人数y之间的关系，经过调查得到如下数据：‎ 调查小组先从这6组数据中选取4组数据求线性回归方程，再用剩下的2组数据进行检验。检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数，再求 与实际等候人数y的差，若差值的绝对值都不超过1，则称所求方程是“恰当回归方程”。‎ ‎(1)从这6组数据中随机选取4组数据，求剩下的2组数据的间隔时间相邻的概率；‎ ‎(2)若选取的是中间4组数据，求y关于x的线性回归方程，并判断此方程是否是“恰当回归方程”。‎ 附：对于一组数据(x1，y1)，(x2，y2)，…，(xn，yn)，其回归直线的斜率和截距的最小二乘估计分别为：。‎ ‎21.(本小题满分12分)‎ 在四棱锥P－ABCD中，底面ABCD是边长为2的正方形，PA⊥底面ABCD，四棱锥P－ABCD的体积V＝，M是PA的中点。‎ ‎ ‎ ‎(1)求异面直线PB与MD所成角的余弦值；‎ ‎(2)求点B到平面PCD的距离。‎ ‎22.(本小题满分12分)‎ 如图，圆x2＋y2＝4与x轴交于A、B两点，动直线l：y＝kx＋1与x轴、y轴分别交于点E、F，与圆交于C、D两点。‎ ‎ ‎ ‎(1)求CD的中点M的轨迹方程；‎ ‎(2)若，求直线l的方程；‎ ‎(3)设直线AD、CB的斜率分别为k1、k2，是否存在实数k使得＝2？若存在，求出k的值；若不存在，说明理由。‎