高中数学 1-5-3 定积分的概念双基限时训练 新人教版选修2-2
【名师一号】2014-2015学年高中数学 1-5-3 定积分的概念双基限时训练 新人教版选修2-2
1.定积分f(x)dx的大小( )
A.与f(x)和积分区间[a,b]有关,与ξi的取法无关
B.与f(x)有关,与区间[a, b]及ξi的取法无关
C.与f(x)及ξi的取法有关,与区间[a,b]无关
D.与f(x)、积分区间[a,b]和ξi的取法都有关
答案 A
2.积分dx的值等于( )
A.0 B.1
C. D.2
答案 B
3.当a
0,则f(x)dx的值( )
A.一定是正的
B.一定是负的
C.当00时,
f(x)dx>0.
答案 A
4.直线x=1,x=-1,y=0及曲线y=x3+sin3x围成的平面图形的面积可以表示为( )
A.-1(x3+sin3x)dx B.|-1(x3+sin3x)dx|
C.(x3+sin3x)dx D.2(x3+sin3x)dx
解析 ∵y=x3+sin3x为奇函数,其图象关于原点对称,x轴上方的面积为(x3+sin3x)dx,
∴整个图形的面积为2(x3+sin3x)dx.
答案 D
5.已知[f(x)+g(x)]dx=18,f(x)dx=10,则
g(x)dx等于( )
A.8 B.10
C.18 D.不确定
解析 由定积分的性质可知,g(x)dx=18-10=8.
答案 A
6.已知f(x)dx=6,则6f(x)dx等于__________.
解析 6f(x)dx=6f(x)dx=6×6=36.
答案 36
7.已知x2dx=,x2dx=,则(x2+1)dx=________.
解析 x2dx=x2dx+x2dx=+=.
又1dx=2,
∴(x2+1)dx=x2dx+1dx=+2=.
答案
8.设f(x)在区间[a,b]上连续,则f(x)dx-f(t)dt的值为__________.
答案 0
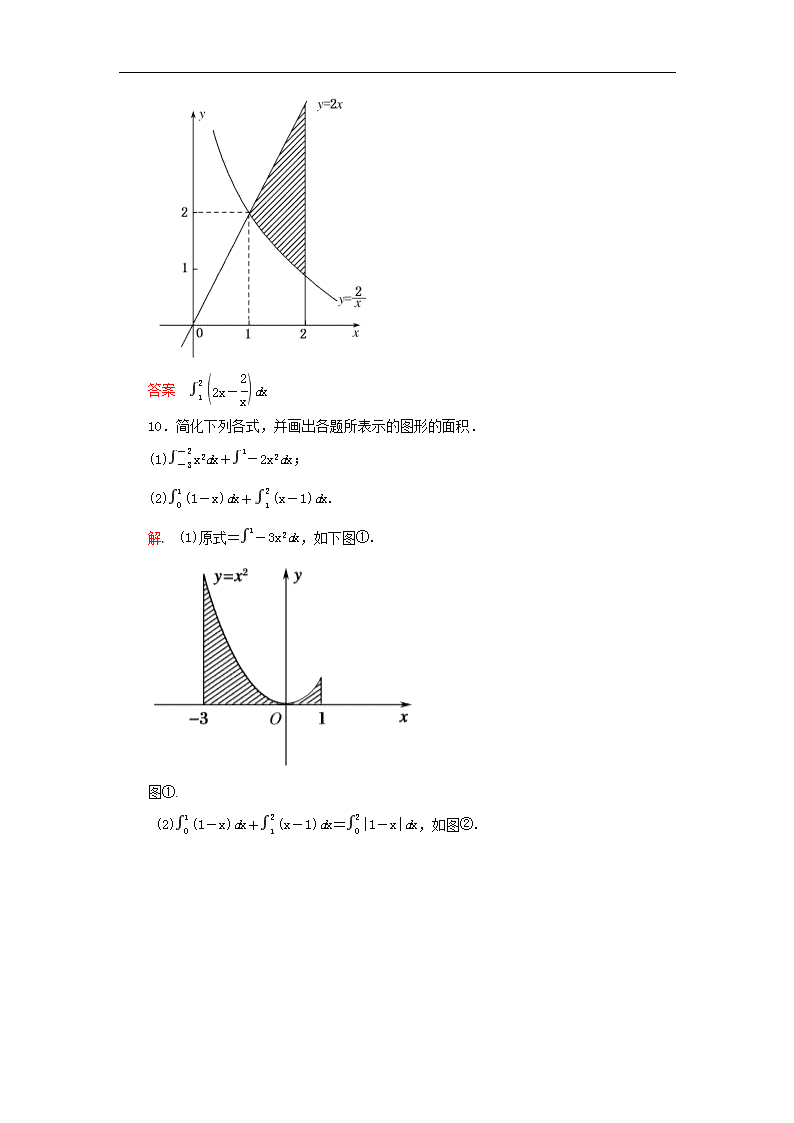
9.曲线y=与直线y=2x,x=2所围成图形的面积用定积分可表示为________.
解析 如图所示,阴影部分面积为
2xdx-dx=dx.
答案 dx
10.简化下列各式,并画出各题所表示的图形的面积.
(1)x2dx+-2x2dx;
(2)(1-x)dx+(x-1)dx.
解 (1)原式=-3x2dx,如下图①.
图①
(2)(1-x)dx+(x-1)dx=|1-x|dx,如图②.
图②
11.已知f(x)为偶函数,且f(x)dx=3,计算定积分
-23f(x)dx.
解 ∵f(x)为偶函数,∴f(x)的图象关于y轴对称,
∴-2f(x)dx=f(x)dx=3.
∴-23f(x)dx=3-2f(x)dx=3[-2f(x)dx+
f(x)dx]=3×(3+3)=18.
12.利用定积分的性质、几何意义求-3(sinx+)dx.
解 -3(sinx+)dx
=-3sinxdx+-3dx.
∵y=sinx在[-3,3]上为奇函数,
∴-3sinxdx=0.
由几何意义可得-3dx=×6=3,
∴-3(sinx+)dx=3.