2022届新高考数学二轮复习艺体生专用课件：第3章 不等式（共2讲）

2022届新高考数学二轮复习艺体生专用课件：第3章 不等式（共2讲）

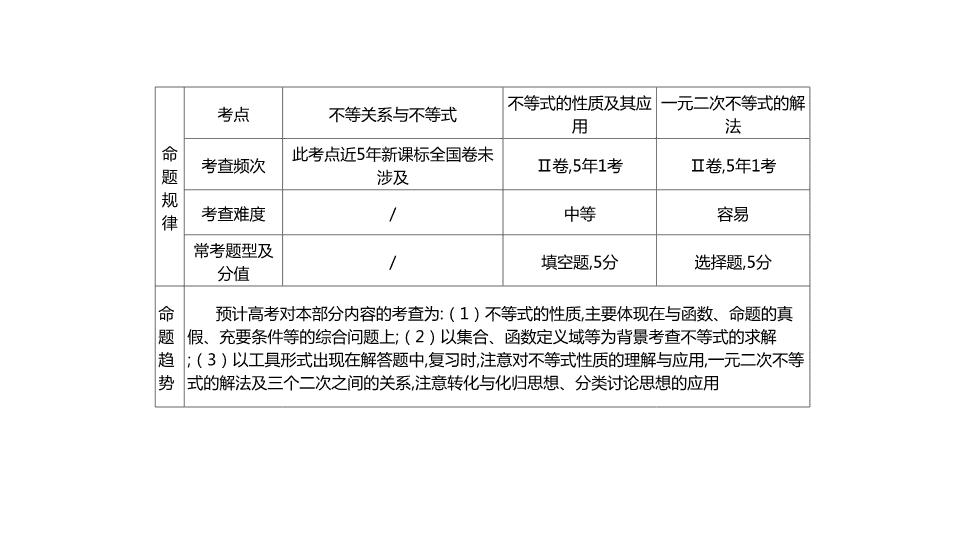
第一节 不等式的性质及一元二次不等式 考情解读 命 题 规 律 考点 不等关系与不等式 不等式的性质及其应 用 一元二次不等式的解 法 考查频次 此考点近5年新课标全国卷未 涉及 Ⅱ卷,5年1考 Ⅱ卷,5年1考 考查难度 / 中等 容易 常考题型及 分值 / 填空题,5分 选择题,5分 命 题 趋 势 预计高考对本部分内容的考查为:（1）不等式的性质,主要体现在与函数、命题的真 假、充要条件等的综合问题上;（2）以集合、函数定义域等为背景考查不等式的求解;（3） 以工具形式出现在解答题中,复习时,注意对不等式性质的理解与应用,一元二次不等式的解 法及三个二次之间的关系,注意转化与化归思想、分类讨论思想的应用 基础导学 知识梳理 4. 一元二次不等式与相应的二次函数及一元二次方程的关系 知识拓展 重难突破 考点一 比较大小 典例研析 【例1】 B B 方法技巧： 作差法适用于四则运算形式的整式型代数式的比较大小问题,是解决比较大小问题的 基本方法;作商法适用于幂指数形式的代数式以及整式的比较大小问题,破解此类题 的关键点： （1）作差（商）,即根据两数或两式的结构特征确定作差或作商. （2）变形,即把差式或商式进行等价变形,化简,以便于判断差或商的大小. （3）定值,即判断差与0的大小,或商与1的大小. （4）定号,即根据差与0的大小关系,或商与1的大小关系确定两数或两式的大小关系. 对点训练 A 重难突破 考点二 不等式的性质 典例研析 【例2】 D 方法技巧： 对点训练 C 重难突破 考点三 一元二次不等式的解法 典例研析 【例3】 方法技巧： 对点训练 C A D 重难突破 考点四 不等式恒成立问题 典例研析 【例4】 A 方法技巧： 对点训练 课时作业 一、单项选择题 D B D C A B C B 二、多项选择题 CD BD 三、填空题 第二节 基本不等式 考情解读 命题 规律 考点 利用基本不等式求最值 基本不等式的综合应用 基本不等式的实际应用 考查频次 5年0考 5年0考 5年0考 考查难度 / / / 常考题型及分值 / / / 命题 趋势 预计高考对本部分的考查以基本不等式的应用为主.复习时,要注意公式的灵活使用,另外,利用基本不等式求最值要 多加强训练 基础导学 知识梳理 算术平均数 几何平均数 知识梳理 最小值 积定和最小 最大值 和定积最大 知识拓展 重难突破 考点一 利用基本不等式求最值 典例研析 考查角度一 配凑 【例1】 5 0 方法技巧： 【例2】 C 方法技巧： 考查角度三 减元 3 本题中出现了三个变元,所以我们要利用题中所给的条件构建不等关系,并减元,在减元后应注意新变元的取值范 围. 方法技巧： 对点训练 D C 5 重难突破 考点二 基本不等式的综合应用 典例研析 【例4】 30 方法技巧： 基本不等式综合应用求解策略 （1）应用基本不等式判断不等式是否成立：对所给不等式（或式子）变形,然后利用基本不等式求解. （2）条件不等式的最值问题;通过条件转化成能利用基本不等式的形式求解. （3）求参数的值或范围：观察题目特点,利用基本不等式确定相关成立条件,从而得到参数的值或范围. 对点训练 A 8 课时作业 一、单项选择题 D C B C C B D B 二、多项选择题 AD BD 三、填空题 4 80