2018届二轮复习 三角函数的图象与性质 课件（全国通用）

2018届二轮复习 三角函数的图象与性质 课件（全国通用）

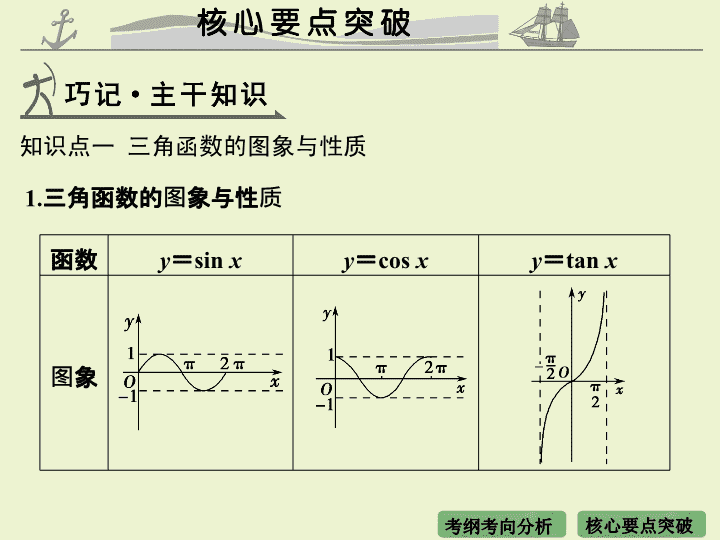
第 二 节　 三角函数的图象与性质 考点梳理 考纲速览 命题解密 热点预测 1. 三角函数的图象及应用 . 2. 三角函数的性质及应用 . 3. 三角函数的图象与性质的综合应用 . 1. 能画出 y ＝ sin x ， y ＝ cos x ， y ＝ tan x 的图象，了解三角函数的周期性 . 2. 了解三角函数 y ＝ A sin( ωx ＋ φ ) 的物理意义；能画出 y ＝ A sin( ωx ＋ φ ) 的图象，了解参数 A 、 ω 、 φ 对函数图象变化的影响 . 3. 理解正弦函数、余弦函数在区间 [0 ， 2 π ] 上的性质 ( 如单调性、最大值和最小值以及与 x 轴的交点等 ) ，理解正切函数在区间 内的单调性 . 　　高考对本部分的考查主要为三角函数的值域、最值、单调性、周期性等，考查学生利用知识分析问题解决问题的能力 . 　　该部分内容仍将作为基础内容出现在综合题中，由于该部分内容基础性较强，备考中应注意基本概念，基本公式的熟练应用，同时应重点训练三角函数的图象与性质 . 知识点一 三角函数的图象与性质 1. 三角函数的图象与性质 函数 y ＝ sin x y ＝ cos x y ＝ tan x 图象 2 k π ( k ∈ Z) π ＋ 2 k π ( k ∈ Z) 偶 x ＝ k π ， k ∈ Z k ∈ Z k ∈ Z x ＝ k π ， k ∈ Z 2 π 2. 周期性 (1) 一般地，对于函数 f ( x ) ，如果存在一个非零常数 T ，使得当 x 取定义域内的每一个值时，都有 f ( x ＋ T ) ＝ f ( x ) ，那么函数 f ( x ) 就叫做周期函数，非零常数 T 叫做这个函数的周期 . (2) 对于一个周期函数 f ( x ) ，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做 f ( x ) 的 ___________ . (3) 函数 y ＝ A sin( ωx ＋ φ ) ， x ∈ R 及函数 y ＝ A cos( ωx ＋ φ ) ， x ∈ R( 其中 A 、 ω 、 φ 为常数，且 A ≠ 0 ， ω ＞ 0) 的周期 T ＝ 最小正周期 知识点二 五点法作图与图象变换 1. 用五点法作正弦函数和余弦函数的简图 ( π ， － 1) 2. y ＝ A sin( ωx ＋ φ ) 的物理意义 3. 用五点法画 y ＝ A sin( ωx ＋ φ ) 一个周期内的简图 用五点法画 y ＝ A sin( ωx ＋ φ ) 一个周期内的简图时，要找五个关键点，如下表所示 . 4. 函数 y ＝ sin x 的图象变换得到 y ＝ A sin( ωx ＋ φ )( A ＞ 0 ， ω ＞ 0) 的图象的步骤 【 名师助学 】 1 . 本部分知识可以归纳为： (1) 四类函数： (2) 五种性质： ① 单调性； ② 最值； ③ 奇偶性； ④ 对称性； ⑤ 周期性 . (3) 两种方法：求三角函数值域的两种方法： ① 图象法：将所给函数化为 y ＝ A sin( ωx ＋ φ ) 的形式 ， 通过分析 ωx ＋ φ 的范围 ， 结合图象写出函数的值域； ② 换元法：把 sin x 或 cos x 看作一个整体 ， 作为二次函数来解决 . 2 . 闭区间上最值或值域问题 ， 首先要在定义域基础上分析单调性 ， 含参数的最值问题 ， 要讨论参数对最值的影响 . 3 . 求三角函数的单调区间时 ， 应先把函数式化成形如 y ＝ A sin( ωx ＋ φ )( ω >0) 的形式 ， 再根据基本三角函数的单调区间 ， 求出 x 所在的区间 . 方法 1 三角函数的图象 函数 y ＝ A sin( ωx ＋ φ )( A ＞ 0 ， ω ＞ 0) 的图象的作法 [ 点评 ] 　 五点作图取值要准确 ， 一般取一个周期之内的；函数图象变换要注意顺序 ， 平移时两种平移的单位长度不同 . 方法 2 三角函数的性质 三角函数 f ( x ) ＝ A sin( ωx ＋ φ ) 的对称性、奇偶性与周期性综合问题的处理应充分关注： [ 点评 ] 　 解决本题的关键是准确的化简出函数 f ( x ) 的解析式 . 方法 3 求三角函数的值域（最值）问题 求三角函数的值域 ( 最值 ) 的常见类型及方法 (1) 形如 y ＝ a sin x ＋ b cos x ＋ c 的三角函数化为 y ＝ A sin( ωx ＋ φ ) ＋ k 的形式，再求最值 ( 值域 ) ； (2) 形如 y ＝ a sin 2 x ＋ b sin x ＋ c 的三角函数，可先设 sin x ＝ t ，化为关于 t 的二次函数求值域 ( 最值 ) ； (3) 形如 y ＝ a sin x cos x ＋ b (sin x ± cos x ) ＋ c 的三角函数，可先设 t ＝ sin x ± cos x ，化为关于 t 的二次函数求值域 ( 最值 ). [ 点评 ] 　 三角函数值域的不同求法 (1) 利用 sin x 和 cos x 的值域直接求 . (2) 把所给的三角函数式变换成 y ＝ A sin( ωx ＋ φ ) 的形式求值域 . (3) 把 sin x 或 cos x 看做一个整体 ， 转换成二次函数求值域 . (4) 利用 sin x ±cos x 和 sin x cos x 的关系转换成二次函数求值域 .