2020-2021学年数学新教材人教A版选择性必修第一册教案：第2章 章末综合提升

2020-2021学年数学新教材人教A版选择性必修第一册教案：第2章 章末综合提升

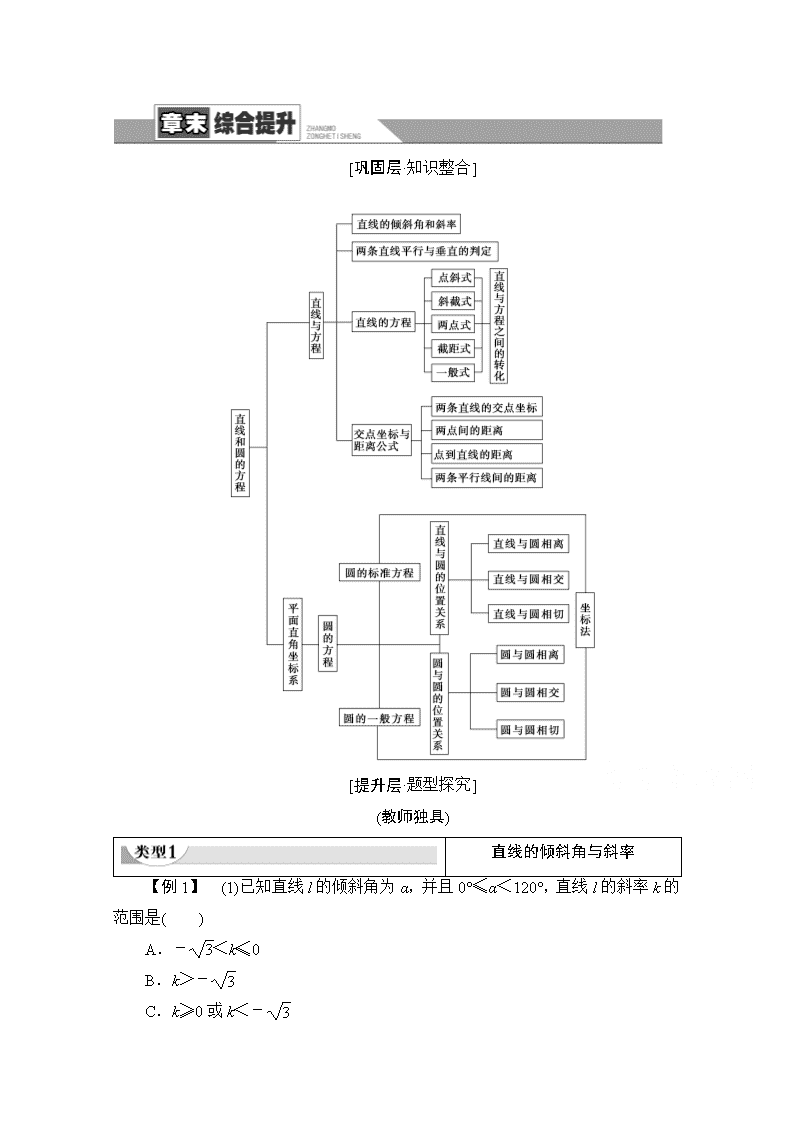
www.ks5u.com ‎[巩固层·知识整合] ‎ ‎[提升层·题型探究]‎ ‎(教师独具)‎ 直线的倾斜角与斜率 ‎【例1】　(1)已知直线l的倾斜角为α，并且0°≤α＜120°，直线l的斜率k的范围是(　　)‎ A．－＜k≤0‎ B．k＞－ C．k≥0或k＜－ D．k≥0或k＜－ ‎(2)已知某直线l的倾斜角α＝45°，又P1(2，y1)，P2(x2,5)，P3(3,1)是此直线上的三点，求x2，y1的值．‎ ‎(1)C　[通过画图可知k＜－或k≥0.故选C.]‎ ‎(2)[解]　由α＝45°，故直线l的斜率k＝tan 45°＝1，‎ 又P1，P2，P3都在此直线上，故kP1P2＝kP2P3＝kl，‎ 即＝＝1，解得x2＝7，y1＝0.‎ 求直线的倾斜角与斜率的注意点 ‎(1)求直线的倾斜角，关键是依据平面几何的知识判断直线向上方向与x轴正向之间所成的角，同时应明确倾斜角的范围．‎ ‎(2)当直线的倾斜角α∈[0°，90°)时，随着α的增大，直线的斜率k为非负值且逐渐变大；当直线的倾斜角α∈(90°，180°)时，随着α的增大，直线的斜率k为负值且逐渐变大．‎ ‎[跟进训练]‎ ‎1．已知直线ax＋y＋2＝0及两点P(－2,1)，Q(3,2)，若直线与线段PQ相交，则实数a的取值范围是(　　)‎ A．a≤－或a≥ B．a≤－或a≥ C．－≤a≤ D．－≤a≤ A　[因为直线ax＋y＋2＝0过定点A(0，－2)，根据题意画出几何图形如图所示：‎ 直线ax＋y＋2＝0可化为y＝－ax－2，因为P(－2,1)，Q(3,2)，‎ 则kAP＝＝－，kAQ＝＝.‎ 若直线y＝－ax－2与线段PQ相交，‎ 即－a≥或－a≤－，‎ 所以a≤－或a≥.]‎ 求直线的方程 ‎【例2】　已知△ABC的顶点A(5,1)，AB边上的中线CM所在的直线方程为2x－y－5＝0，AC边上的高BH所在的直线方程为x－2y－5＝0.‎ 求：(1)AC所在的直线的方程；‎ ‎(2)点B的坐标．‎ ‎[思路探究]　(1)直线AC过A点且与BH垂直，可求直线方程．‎ ‎(2)B点在直线BH上，线段AB的中点在中线CM上，列方程组求得B点坐标．‎ ‎[解]　(1)因为AC⊥BH，所以设AC所在的直线的方程为2x＋y＋t＝0.‎ 把A(5,1)代入直线方程2x＋y＋t＝0中，解得t＝－11.‎ 所以AC所在的直线的方程为2x＋y－11＝0.‎ ‎(2)设B(x0，y0)，则AB的中点为.‎ 联立得方程组 化简得解得故B(－1，－3)．‎ 求直线方程的方法 求直线方程的主要方法是待定系数法，要掌握直线方程五种形式的适用条件及相互转化，能根据条件灵活选用方程，当不能确定某种方程条件是否具备时要另行讨论条件不满足的情况．‎ ‎[跟进训练]‎ ‎2．已知△ABC中，A(1,3)，AB，AC边上中线所在直线方程分别为x－2y ‎＋1＝0和y－1＝0，求△ABC各边所在的直线方程. ‎ ‎[解]　设AB，AC边上的中线分别为CD，BE，其中D，E为中点， ‎ ‎∵点B在中线y－1＝0上， ‎ ‎∴设点B的坐标为(xB,1)．‎ ‎∵点D为AB的中点，又点A的坐标为(1,3)，‎ ‎∴点D的坐标为.‎ ‎∵点D在中线CD：x－2y＋1＝0上，‎ ‎∴－2×2＋1＝0，∴xB＝5.‎ ‎∴点B的坐标为(5,1)．‎ ‎∵点C在直线x－2y＋1＝0上，‎ ‎∴设点C的坐标为(2t－1，t)．‎ ‎∴AC的中点E的坐标为.‎ ‎∵点E在中线BE：y＝1上，‎ ‎∴＝1，∴t＝－1.‎ ‎∴点C的坐标为(－3，－1)，‎ ‎∴△ABC各边所在直线的方程为AB：x＋2y－7＝0，‎ BC：x－4y－1＝0，AC：x－y＋2＝0.‎ 两直线的平行、垂直及距离问题 ‎【例3】　已知两条直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0，求分别满足下列条件的a，b的值．‎ ‎(1)直线l1过点(－3，－1)，并且直线l1与直线l2垂直；‎ ‎(2)直线l1与直线l2平行，并且坐标原点到l1，l2的距离相等．‎ ‎[思路探究]　(1)把(－3，－1)代入l1方程，同时运用垂直条件A1A2＋B1B2＝0；(2)利用好平行条件及距离公式列方程．‎ ‎[解]　(1)∵l1⊥l2，‎ ‎∴a(a－1)＋(－b)·1＝0.‎ 即a2－a－b＝0.①‎ 又点(－3，－1)在l1上，‎ ‎∴－3a＋b＋4＝0.②‎ 由①②解得a＝2，b＝2.‎ ‎(2)∵l1∥l2且l2的斜率为1－a，‎ ‎∴l1的斜率也存在，＝1－a，‎ 即b＝.‎ 故l1和l2的方程可分别表示为 l1：(a－1)x＋y＋＝0，‎ l2：(a－1)x＋y＋＝0.‎ ‎∵原点到l1与l2的距离相等，‎ ‎∴4＝，解得a＝2或a＝.‎ 因此或 距离公式的运用 ‎(1)距离问题包含两点间的距离，点到直线的距离，两平行直线间的距离．‎ ‎(2)牢记各类距离的公式并能直接应用，解决距离问题时，往往将代数运算与几何图形的直观分析相结合．‎ ‎(3)这类问题是高考考查的热点，在高考中常以选择题、填空题出现，主要考查距离公式以及思维能力．‎ ‎[跟进训练]‎ ‎3．已知直线l经过直线2x＋y－5＝0与x－2y＝0的交点．‎ ‎(1)点A(5,0)到l的距离为3，求l的方程；‎ ‎(2)求点A(5,0)到l的距离的最大值．‎ ‎[解]　(1)经过两已知直线交点的直线系方程为2x＋y－5＋λ(x－2y)＝0, 即(2＋λ)x＋(1－2λ)y－5＝0，‎ 所以＝3，‎ 即2λ2－5λ＋2＝0，所以λ＝或λ＝2.‎ 所以l的方程为x＝2或4x－3y－5＝0.‎ ‎(2)由解得交点P(2,1)，过P作任一直线l(图略)，设d为点A到l的距离，则d≤|PA|(当l⊥PA时等号成立)．‎ 所以dmax＝|PA|＝.‎ 对称问题 ‎[探究问题]‎ ‎1．怎样求点关于点的对称点？‎ ‎[提示]　设出所求点坐标，利用中点坐标公式求解．‎ ‎2．怎样求点关于直线的对称点坐标？‎ ‎[提示]　设出所求点坐标(x, y)，利用中点坐标公式建立关于x, y的第一个方程，再利用垂直关系建立x, y的另一个方程，然后通过联立方程解二元一次方程组求解．‎ ‎【例4】　光线通过点A(2, 3)，在直线l：x＋y＋1＝0上反射，反射光线经过点B(1,1)，试求入射光线和反射光线所在直线的方程．‎ ‎[解]　设点A(2,3)关于直线l的对称点为A′(x0，y0)，则 解之得，A′(－4，－3)．‎ 由于反射光线经过点A′(－4，－3)和B(1,1)，‎ 所以反射光线所在直线的方程为 y－1＝(x－1)·，即4x－5y＋1＝0.‎ 解方程组得反射点P.‎ 所以入射光线所在直线的方程为 y－3＝(x－2)·，即5x－4y＋2＝0.‎ 综上，入射光线和反射光线所在直线的方程分别为5x－4y＋2＝0,4x－5y＋1＝0.‎ ‎1．[变结论]在本例条件不变的情况下，求光线从A经反射后到达B点所经过的路程．‎ ‎[解]　由本例解析知，点A(2,3)关于直线l的对称点为A′(－4，－3)．所以从A发出光线经l反射后到达B的路程为|A′B|.‎ 即|A′B|＝＝.‎ ‎2．[变条件]把本例条件中“直线l：x＋y＋1＝0”改为“直线l为x轴”，其他条件不变，试求入射光线和反射光线所在直线的方程．‎ ‎[解]　点A(2,3)关于x轴对称点为A′(2，－3)．‎ ‎∴反射光线方程为＝，即4x＋y－5＝0.‎ 又∵反射光线与x轴交点为.‎ ‎∴入射光线方程为＝，‎ 即4x－y－5＝0.‎ 对称问题的求解策略 ‎(1)点关于点的对称问题，是对称问题中最基础最重要的一类，其余几类对称问题均可以化归为点关于点的对称进行求解．熟练掌握和灵活运用中点坐标公式是处理这类问题的关键．‎ ‎(2)点关于直线的对称问题是点关于点的对称问题的延伸，处理这类问题主要抓住两个方面：①两点连线与已知直线斜率乘积等于－1；②两点的中点在已知直线上．‎ ‎(3)直线关于点的对称问题，可转化为直线上的点关于此点对称的问题，这里需要注意的是两对称直线是平行的．我们往往利用平行直线系去求解．‎ 求圆的方程 ‎【例5】　已知圆C和y轴相切，圆心在直线x－3y＝0上，且被直线y＝x 截得的弦长为2，求圆C的方程．‎ ‎[思路探究]　设标准方程，由相切可得d＝r，由圆心在直线上，可将(a，b)代入直线方程，由已知弦长可列出弦长公式．通过方程组求解，从而得到圆的方程．‎ ‎[解]　设圆C的方程为(x－a)2＋(y－b)2＝r2.‎ 由圆C与y轴相切得|a|＝r，①‎ 又圆心在直线x－3y＝0上，‎ ‎∴a－3b＝0，②‎ 圆心C(a，b)到直线y＝x的距离为d＝，由于弦心距d，半径r及弦的一半构成直角三角形，‎ ‎∴＋()2＝r2.③‎ 联立①②③解方程组可得或 故圆C的方程为(x－3)2＋(y－1)2＝9或(x＋3)2＋(y＋1)2＝9.‎ ‎1．求圆的方程的方法 求圆的方程主要是联立圆系方程、圆的标准方程和一般方程，利用待定系数法解题．‎ ‎2．采用待定系数法求圆的方程的一般步骤 ‎(1)选择圆的方程的某一形式．‎ ‎(2)由题意得a, b, r(或D, E, F)的方程(组)．‎ ‎(3)解出a, b, r(或D, E, F)．‎ ‎(4)代入圆的方程．‎ ‎[跟进训练]‎ ‎4．已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数且与直线4x＋3y－29＝0相切，求圆的方程．‎ ‎[解]　设圆心为M(m,0)(m∈Z)，‎ 由于圆与直线4x＋3y－29＝0相切，且半径为5，‎ 所以＝5，‎ 即|4m－29|＝25，‎ 因为m为整数，故m＝1，‎ 故所求圆的方程为(x－1)2＋y2＝25.‎ 直线与圆的位置关系 ‎【例6】　如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2＋y2－12x－14y＋60＝0及其上一点A(2,4)．‎ ‎(1)设圆N与x轴相切，与圆M外切，且圆心N在直线x＝6上，求圆N的标准方程；‎ ‎(2)设平行于OA的直线l与圆M相交于B，C两点，且BC＝OA，求直线l的方程．‎ ‎[思路探究]　(1)根据圆与x轴相切确定圆心位置，再根据两圆外切建立等量关系求半径；(2)根据垂径定理确定等量关系，求直线方程．‎ ‎[解]　圆M的标准方程为(x－6)2＋(y－7)2＝25，所以圆心M(6,7)，半径为5.‎ ‎(1)由圆心N在直线x＝6上，可设N(6，y0)．因为N与x轴相切，与圆M外切，所以0＜y0＜7，于是圆N的半径为y0，从而7－y0＝5＋y0，解得y0＝1.‎ 因此，圆N的标准方程为(x－6)2＋(y－1)2＝1.‎ ‎(2)因为直线l∥OA，所以直线l的斜率为＝2.‎ 设直线l的方程为y＝2x＋m，即2x－y＋m＝0，‎ 则圆心M到直线l的距离 d＝＝.‎ 因为BC＝OA＝＝2，而MC2＝d2＋，‎ 所以25＝＋5，解得m＝5或m＝－15.‎ 故直线l的方程为2x－y＋5＝0或2x－y－15＝0.‎ 判断直线和圆的位置关系，一般用代数法或几何法，为避免繁杂的运算，最好用几何法，其解题思路是：先求出圆心到直线的距离d，然后比较所求距离d与半径r的大小关系，进而判断直线和圆的位置关系．‎ ‎[跟进训练]‎ ‎5．已知直线l：2mx－y－8m－3＝0和圆C：x2＋y2－6x＋12y＋20＝0.‎ ‎(1)m∈R时，证明l与C总相交；‎ ‎(2)m取何值时，l被C截得的弦长最短，求此弦长．‎ ‎[解]　(1)证明：直线的方程可化为y＋3＝2m(x－4)，‎ 由点斜式可知，直线过点P(4, －3)．‎ 由于42＋(－3)2－6×4＋12×(－3)＋20＝－15<0，‎ 所以点P在圆内，故直线l与圆C总相交．‎ ‎(2)如图，当圆心C(3, －6)到直线l的距离最大时，线段AB的长度最短．‎ 此时PC⊥l，所以直线l的斜率为－，所以m＝－.‎ 在△APC中，|PC|＝，|AC|＝r＝5，‎ 所以|AP|2＝|AC|2－|PC|2＝25－10＝15，‎ 所以|AP|＝，所以|AB|＝2，‎ 即最短弦长为2.‎ 圆与圆的位置关系 ‎【例7】　已知圆C1：x2＋y2＋4x－4y－5＝0与圆C2：x2＋y2－8x＋4y＋7＝0.‎ ‎(1)证明圆C1与圆C2相切，并求过切点的两圆公切线的方程；‎ ‎(2)求过点(2, 3)且与两圆相切于(1)中切点的圆的方程．‎ ‎[解]　(1)把圆C1与圆C2都化为标准方程形式，得(x＋2)2＋(y－2)2＝13，(x－4)2＋(y＋2)2＝13.‎ 圆心与半径长分别为C1(－2,2)，r1＝；‎ C2(4，－2)，r2＝.‎ 因为|C1C2|＝＝2＝r1＋r2，‎ 所以圆C1与圆C2相切．‎ 由得12x－8y－12＝0，‎ 即3x－2y－3＝0，就是过切点的两圆公切线的方程．‎ ‎(2)由圆系方程，可设所求圆的方程为 x2＋y2＋4x－4y－5＋λ(3x－2y－3)＝0.‎ 点(2, 3)在此圆上，将点坐标代入方程解得λ＝.‎ 所以所求圆的方程为x2＋y2＋4x－4y－5＋(3x－2y－3)＝0，即x2＋y2＋8x－y－9＝0.‎ 判断两圆位置关系的两种方法比较 ‎(1)几何法是利用两圆半径和或差与圆心距作比较，得到两圆位置关系．‎ ‎(2)代数法是把两圆位置关系的判断完全转化为代数问题，转化为方程组解的组数问题，从而体现了几何问题与代数问题之间的相互联系，但这种方法只能判断出不相交、相交和相切三种位置关系，而不能像几何法一样，能准确判断出外离、外切、相交、内切和内含五种位置关系．‎ ‎[跟进训练]‎ ‎6.在平面直角坐标系xOy中，过点P(0,1)且互相垂直的两条直线分别与圆O：x2＋y2＝4交于点A，B，与圆M：(x－2)2＋(y－1)2＝1交于点C，D.若AB＝，求CD的长．‎ ‎[解]　因为AB＝，圆O半径为2，‎ 所以点O到直线AB的距离为，显然AB，CD都不平行于坐标轴．‎ 可知AB：y＝kx＋1，即kx－y＋1＝0.‎ 则点O到直线AB的距离d＝＝，解得k＝±.‎ 因为AB⊥CD，所以kCD＝－，‎ 所以CD：y＝－x＋1，即x＋ky－k＝0.‎ 点M(2,1)到直线CD的距离d′＝＝，‎ 所以CD＝2＝2＝.‎ ‎[培优层·素养升华]‎ ‎【例】　已知圆C：x2＋y2＋2x－7＝0内一点P(－1,2)，直线l过点P且与圆C交于A，B两点．‎ ‎(1)求圆C的圆心坐标和面积；‎ ‎(2)若直线l的斜率为，求弦AB的长；‎ ‎(3)若圆上恰有三点到直线l的距离等于，求直线l的方程．‎ ‎[思路探究]　(1)化圆的一般式为标准方程，得出圆C的圆心坐标为(－1,0)，半径r＝2即可．‎ ‎(2)先求圆心到直线的距离为d，再利用半径r，距离d，半弦长构成直角三角形求解即可．‎ ‎(3)圆上恰有三点到直线l的距离等于，等价于圆心(－1,0)到直线AB 的距离为＝，利用点到直线的距离公式求解．‎ ‎[解]　(1)圆C的圆心坐标为(－1,0)，半径r＝2，面积为S＝8π.‎ ‎(2)直线l的方程为y－2＝(x＋1)，即x－y＋2＋＝0，‎ 圆心到直线l的距离为d＝＝1，|AB|＝2＝2＝2.‎ ‎(3)因圆上恰有三点到直线l的距离等于，转化为 圆心(－1,0)到直线AB的距离为＝，‎ 当直线l垂直于x轴时，‎ 显然不合题意；‎ 设直线l的方程为y－2＝k(x＋1)，‎ 即kx－y＋2＋k＝0，‎ 由d＝＝＝，‎ 解得k＝±1，‎ 故直线l的方程为x－y＋3＝0，或x＋y－1＝0.‎ ‎1.本题反映的是本章的重点热点问题，综合考查了圆的方程、直线的方程、距离公式、两直线的位置关系及直线与圆的位置关系．‎ ‎2．通过考查这些知识点和题型，培养了学生直观想象，逻辑推理，数学建模、数学运算的核心素养．‎ ‎3．本题考查知识点全面且基本，属中档题．‎ ‎[跟进训练]‎ ‎7．已知圆x2＋y2－4ax＋2ay＋20a－20＝0.‎ ‎(1)求证：对任意实数a，该圆恒过一定点；‎ ‎(2)若该圆与圆x2＋y2＝4相切，求a的值．‎ ‎[解]　(1)证明：圆的方程可整理为 ‎(x2＋y2－20)＋a(－4x＋2y＋20)＝0，‎ 此方程表示过圆x2＋y2－20＝0和直线－4x＋2y＋20＝0交点的圆系．‎ 由 得 ‎∴已知圆过定点(4，－2)．‎ ‎(2)圆的方程可化为(x－2a)2＋(y＋a)2＝5(a－2)2.‎ ‎①当两圆外切时，d＝r1＋r2，‎ 即2＋＝，‎ 解得a＝1＋或a＝1－(舍去)；‎ ‎②当两圆内切时，d＝|r1－r2|，‎ 即|－2|＝，‎ 解得a＝1－或a＝1＋(舍去)．‎ 综上所述，a＝1±.‎