2018-2019学年贵州省铜仁一中高二下学期开学考试数学（理科）试题（Word版）

2018-2019学年贵州省铜仁一中高二下学期开学考试数学（理科）试题（Word版）

铜仁一中2018—2019学年度第二学期高二开学考试 ‎ 数学试题（理科） ‎ 注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卡的相应位置。答案写在试卷上均无效，不予记分。‎ 第I卷 ‎ 一、选择题（本大题共12小题，共60.0分）‎ 1. 将二进制数‎11100‎‎(2)‎‎ ‎转化为四进制数，正确的是‎(‎　　‎‎)‎ A. ‎120‎‎(4)‎ B. ‎200‎‎(4)‎ C. ‎130‎‎(4)‎ D. ‎‎202‎‎(4)‎ 2. 我国古代数学名著‎《‎九章算术‎》‎有“米谷粒分”题：粮仓开仓收粮，有人送来米1524石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为‎(‎　　‎‎)‎ A. 134石 B. 168石 C. 338石 D. 1365石 3. 用秦九韶算法求多项式f(x)=x‎5‎+4x‎4‎+x‎2‎+20x+16‎在x=-2‎时，v‎2‎的值为‎(‎    ‎‎)‎ A. 2 B. ‎-4‎ C. 4 D. ‎‎-3‎ 4. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植‎.‎不同的种植方法共有‎(‎　　‎‎)‎ A. 24种 B. 18种 C. 12种 D. 6种 5. ‎(‎x‎+‎ y‎)(2‎x‎-‎ y‎)‎‎5‎的展开式中x‎ ‎‎3‎y‎ ‎‎3‎的系数为‎(‎   ‎‎)‎ A. ‎-80‎ B. ‎-40‎ C. 40 D. 80‎ 6. 如图，正方形ABCD内的图形来自中国古代的太极图‎.‎正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称‎.‎在正方形内随机取一点，则此点取自黑色部分的概率是‎(‎　　‎‎)‎ A. ‎1‎‎4‎ ‎ B. π‎8‎ C. ‎1‎‎2‎ ‎ D. 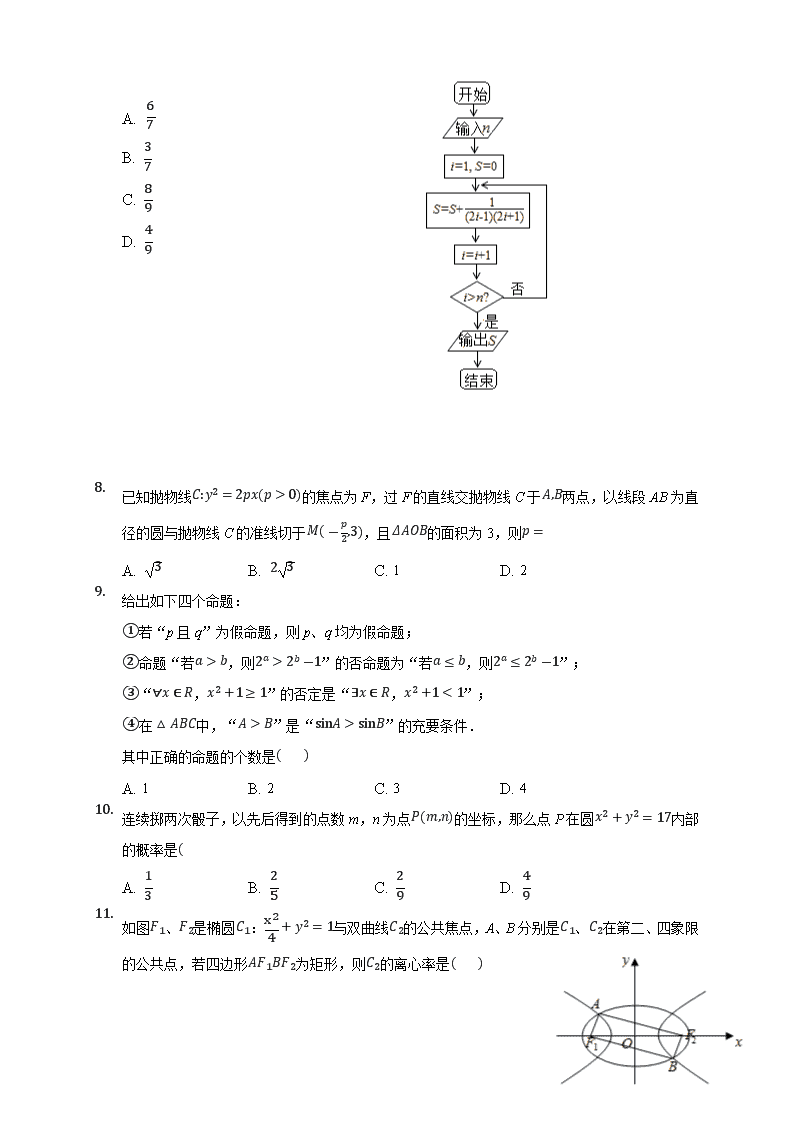‎π‎4‎ 7. 执行如图所示的程序框图，如果输入n=4‎，则输出的S=(‎　　‎)‎ ‎ A. ‎6‎‎7‎‎ ‎ B. ‎‎3‎‎7‎ C. ‎8‎‎9‎ ‎ D. ‎‎4‎‎9‎ ‎ ‎ 1. 已知抛物线C:y‎2‎=2px(p>0)‎的焦点为F，过F的直线交抛物线C于A,B两点，以线段AB为直径的圆与抛物线C的准线切于M(-p‎2‎,3)‎，且ΔAOB的面积为3，则p=‎ A. ‎3‎ B. ‎2‎‎3‎ C. 1 D. 2‎ 2. 给出如下四个命题： ‎①‎若“p且q”为假命题，则p、q均为假命题； ‎②‎命题“若a>b，则‎2‎a‎>‎2‎b-1‎”的否命题为“若a≤b，则‎2‎a‎≤‎2‎b-1‎”； ‎③‎“‎∀x∈R，x‎2‎‎+1≥1‎”的否定是“‎∃x∈R，x‎2‎‎+1<1‎”； ‎④‎在‎△ABC中，“A>B”是“sinA>sinB”的充要条件． 其中正确的命题的个数是‎(‎　　‎‎)‎ A. 1 B. 2 C. 3 D. 4‎ 3. 连续掷两次骰子，以先后得到的点数m，n为点P(m,n)‎的坐标，那么点P在圆x‎2‎‎+y‎2‎=17‎内部的概率是‎(‎　　‎ A. ‎1‎‎3‎ B. ‎2‎‎5‎ C. ‎2‎‎9‎ D. ‎‎4‎‎9‎ 4. 如图F‎1‎、F‎2‎是椭圆C‎1‎：x‎2‎‎4‎‎+y‎2‎=1‎与双曲线C‎2‎的公共焦点，A、B分别是C‎1‎、C‎2‎在第二、四象限的公共点，若四边形AF‎1‎BF‎2‎为矩形，则C‎2‎的离心率是‎(‎　　‎‎)‎ A. ‎2‎ B. ‎3‎ ‎ C. ‎3‎‎2‎ D. ‎‎6‎‎2‎ 1. 设a，b是关于t的方程t‎2‎cosθ+tsinθ=0‎的两个不等实根，则过A(a,a‎2‎)‎，B(b,b‎2‎)‎两点的直线与双曲线x‎2‎cos‎2‎θ‎-y‎2‎sin‎2‎θ=1‎的公共点的个数为‎(‎　　‎‎)‎ A. 0 B. 1 C. 2 D. 3‎ 第II卷 二、填空题（本大题共4小题，共20.0分）‎ 2. 某地区气象台统计，该地区下雨的概率是‎4‎‎15‎，刮风的概率是‎2‎‎5‎，既刮风又下雨的概率为‎1‎‎10‎，现该地区开始刮风，则该地区会下雨的概率为__________．‎ 3. 已知椭圆C‎:x‎2‎a‎2‎+y‎2‎b‎2‎=1a>b>0‎ ‎的右焦点为F‎,‎以F为圆心的圆：x‎2‎‎+y‎2‎-4x-32=0 ‎恰好与椭圆的右准线相切，则该椭圆的离心率为          ．‎ 4. 已知抛物线‎ x‎2‎=4y ‎的焦点F和点A(-1,8)‎，点P为抛物线上一点，则‎|PA|+|PF|‎的最小值为______ ．‎ 5. 下列说法中，正确的序号是__________．‎ ‎①.‎命题“若am‎2‎sinB”是“A>B”的充要条件．‎ 三、解答题（本大题共6小题，第17题10分，其余每题12分，共70分）‎ 1. 已知‎(x+‎‎1‎‎2‎x‎)‎n的展开式中的第二项和第三项的系数相等． ‎(1)‎求n的值； ‎(2)‎求展开式中所有二项式系数的和； ‎(3)‎求展开式中所有的有理项． ‎ 2. 随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚‎.‎车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题‎.‎某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y(‎万元‎)‎有如表的数据资料：‎ 使用年限x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 总费用y ‎2.2‎ ‎5.5‎ ‎6.5‎ ‎7.0‎ ‎(1)‎在给出的坐标系中做出散点图； ‎(2)‎求线性回归方程y‎=bx+‎a中的a、b； ‎(3)‎估计使用年限为12年时，车的使用总费用是多少？ ‎(‎最小二乘法求线性回归方程系数公式b‎=‎i=1‎nxiyi‎-nxyi=1‎nxi‎2‎‎-nx‎2‎，a‎=y-bx).‎ ‎ 1. 在直角坐标系xOy中，设椭圆C：y‎2‎a‎2‎+x‎2‎b‎2‎=1(a>b>0)‎的上下两个焦点分别为F‎2‎，F‎1‎，过上焦点F‎2‎且与y轴垂直的直线l与椭圆C相交，其中一个交点为‎(-1,‎2‎)‎． ‎(1)‎求椭圆C的方程； ‎(2)‎设椭圆C的一个顶点为B(b,0)‎，直线BF‎2‎交椭圆C于另一个点N，求‎△F‎1‎BN的面积．‎ 2. 设函数f(x)=x‎2‎+2ax-b‎2‎+4‎． ‎(‎Ⅰ‎)‎若a是从‎-2‎、‎-1‎、0、1、2五个数中任取的一个数，b是从0、1、2三个数中任取的一个数，求函数f(x)‎无零点的概率； ‎(‎Ⅱ‎)‎若a是从区间‎[-2,2]‎任取的一个数，b是从区间‎[0,2]‎任取的一个数，求函数f(x)‎无零点的概率． ‎ ‎ ‎ 3. 现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择‎.‎为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．‎ ‎(1)‎求这4个人中恰有2人去参加甲游戏的概率；‎ ‎(2)‎求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；‎ ‎(3)‎用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ζ=‎X-Y，求随机变量ζ的分布列与数学期望Eζ． ‎ ‎ ‎ ‎ ‎ 1. 已知中心在原点，对称轴为坐标轴的椭圆C的一个焦点F在抛物线y‎2‎‎=4x的准线上，且椭圆C过点P(1,‎3‎‎2‎)‎，直线与椭圆C交于A，B两个不同点． ‎(1)‎求椭圆C的方程； ‎(2)‎若直线的斜率为‎1‎‎2‎，且不过点P，设直线PA，PB的斜率分别为k‎1‎，k‎2‎，求证：k‎1‎‎+‎k‎2‎为定值． ‎ 高二下学期开学检测（理）‎ 答案和解析 ‎【答案】‎ ‎1. C 2. B 3. B 4. B 5. C 6. B 7. D 8. A 9. C 10. C 11. D 12. A ‎ ‎13. ‎1‎‎4‎  ‎ ‎14. ‎1‎‎2‎  ‎ ‎15. 9  ‎ ‎16. ‎④‎  ‎ ‎17. 解：二项式‎(x+‎‎1‎‎2‎x‎)‎n展开式的通项公式为 Tr+1‎‎=Cnr⋅xn-r⋅(‎1‎‎2‎x‎)‎r=Cnr⋅(‎1‎‎2‎‎)‎r⋅‎xn-‎3‎‎2‎r，‎(r=0,‎1，2，‎…‎，n)‎； ‎(1)‎根据展开式中的第二项和第三项的系数相等，得 Cn‎1‎‎⋅‎1‎‎2‎=Cn‎2‎⋅(‎‎1‎‎2‎‎)‎‎2‎，即‎1‎‎2‎n=‎1‎‎4‎⋅‎n(n-1)‎‎2‎， 解得n=5‎； ‎(2)‎展开式中所有二项式系数的和为 C‎5‎‎0‎‎+C‎5‎‎1‎+C‎5‎‎2‎+…+C‎5‎‎5‎=‎2‎‎5‎=32‎； ‎(3)‎二项式展开式的通项公式为 Tr+1‎‎=C‎5‎r⋅(‎1‎‎2‎‎)‎r⋅‎x‎5-‎3‎‎2‎r，‎(r=0,‎1，2，‎…‎，‎5)‎； 当r=0‎，2，4时，对应项是有理项， 所以展开式中所有的有理项为 T‎1‎‎=C‎5‎‎0‎⋅(‎1‎‎2‎‎)‎‎0‎⋅x‎5‎=‎x‎5‎， T‎3‎‎=C‎5‎‎2‎⋅(‎1‎‎2‎‎)‎‎2‎⋅x‎5-3‎=‎‎5‎‎2‎x‎2‎， T‎5‎‎=C‎5‎‎4‎⋅(‎1‎‎2‎‎)‎‎4‎x‎5-6‎=‎‎5‎‎16x．  ‎ ‎18. 解：‎(1)‎散点图如图，由图知y与x间有线性相关关系． ； ‎(2)∵x=4‎，y‎=5‎，i=1‎‎5‎xiyi‎=112.3‎，i=1‎‎5‎xi‎2‎‎=90‎， ‎∴b=‎112.3-5×4×5‎‎90-5×‎‎4‎‎2‎=‎12.3‎‎10‎=1.23‎； a‎=y-bx=5-1.23×4=0.08‎． ‎(3)‎线性回归直线方程是y‎=1.23x+0.08‎， 当x=12(‎年‎)‎时，y‎=1.23×12+0.08=14.84(‎万元‎)‎． 即估计使用12年时，支出总费用是‎14.84‎万元．  ‎ ‎19. 解：‎(1)‎椭圆C：y‎2‎a‎2‎+x‎2‎b‎2‎=1(a>b>0)‎的上下两个焦点分别为F‎2‎，F‎1‎，过上焦点F‎2‎且与y轴垂直的直线l与椭圆C相交，其中一个交点为‎(-1,‎2‎).c=‎2‎=‎a‎2‎‎-‎b‎2‎，‎2‎a‎2‎‎+‎1‎b‎2‎=1‎， 解得a‎2‎‎=4‎，b‎2‎‎=2‎， ‎∴‎椭圆C的方程为：y‎2‎‎4‎‎+x‎2‎‎2‎=1‎． ‎(2)‎直线BF‎2‎的方程为x+y-‎2‎=0‎， 由y=-x+‎‎2‎y‎2‎‎+2x‎2‎=4‎，得点N的横坐标为xN‎=-‎‎2‎‎3‎， 又‎|F‎1‎F‎2‎|=2‎‎2‎， ‎∴S‎△F‎1‎BN=‎1‎‎2‎|F‎1‎F‎2‎||xB-xN|=‎1‎‎2‎×2‎2‎×(‎2‎+‎2‎‎3‎)=‎‎8‎‎3‎， 综上，‎△F‎1‎BN的面积为‎8‎‎3‎．  ‎ ‎20. 解：‎(‎Ⅰ‎)‎函数f(x)=x‎2‎+2ax-b‎2‎+4‎无零点等价于方程x‎2‎‎+2ax-b‎2‎+4=0‎无实根， 可得‎△=(2a‎)‎‎2‎-4(-b‎2‎+4)<0‎，可得a‎2‎‎+b‎2‎<4‎ 记事件A为函数f(x)=x‎2‎+2ax-b‎2‎+4‎无零点， 总的基本事件共有15个： ‎(-2,0)‎，‎(-2,1)‎，‎(-2,2)‎，‎(-1,0)‎，‎(-1,1)‎，‎(-1,2)‎， ‎(0,0)‎，‎(0,1)‎，‎(0,2)‎，‎(1,0)‎，‎(1,1)‎， ‎(1,2)‎，‎(2,0)‎，‎(2,1)‎，‎(2,2)‎，事件A包含6个基本事件， ‎∴P(A)=‎6‎‎15‎=‎2‎‎5‎ ‎‎(‎Ⅱ‎)‎ 如图，试验的全部结果所构成的区域为‎(‎矩形区域‎)‎ 事件A所构成的区域为A={(a,b)|a‎2‎+b‎2‎<4‎且‎(a,b)∈Ω}‎即图中的阴影部分． ‎∴P(A)=SASΩ=‎2π‎8‎=‎π‎4‎．  ‎ ‎21. 解：依题意，这4个人中，每个人去参加甲游戏的概率为‎1‎‎3‎，去参加乙游戏的人数的概率为‎2‎‎3‎ 设“这4个人中恰有i人去参加甲游戏”为事件Ai‎(i=0,‎1，2，3，‎4)‎，‎∴P(Ai)=C‎4‎I(‎1‎‎3‎‎)‎I(‎‎2‎‎3‎‎)‎‎4-I ‎(1)‎这4个人中恰有2人去参加甲游戏的概率为P(A‎2‎)=C‎4‎‎2‎(‎1‎‎3‎‎)‎‎2‎(‎2‎‎3‎‎)‎‎2‎=‎‎8‎‎27‎； ‎(2)‎设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B，则B=A‎3‎∪‎A‎4‎， ‎∴P(B)=P(A‎3‎)+P(A‎4‎)=C‎4‎‎3‎(‎1‎‎3‎‎)‎‎3‎×‎2‎‎3‎+C‎4‎‎4‎(‎1‎‎3‎‎)‎‎4‎=‎‎1‎‎9‎ ‎(3)ξ的所有可能取值为0，2，4，由于A‎1‎与A‎3‎互斥，A‎0‎与A‎4‎互斥，故P(ξ=0)=P(A‎2‎)=‎‎8‎‎27‎ P(ξ=2)=P(A‎1‎)+P(A‎3‎)=‎‎40‎‎81‎，P(ξ=4)=P(A‎0‎)+P(A‎4‎)=‎‎17‎‎81‎ ‎∴ξ的分布列是 ‎ ‎ξ ‎ 0‎ ‎ 2‎ ‎ 4‎ ‎ P ‎  ‎ ‎8‎ ‎27‎ ‎  ‎ ‎40‎ ‎81‎ ‎17‎ ‎81[]‎ 数学期望Eξ=0×‎8‎‎27‎+2×‎40‎‎81‎+4×‎17‎‎81‎=‎‎148‎‎81‎  ‎ ‎22. 解：‎(1)‎抛物线y‎2‎‎=4x的准线方程为x=-1‎，由题意知F(-1,0)‎． 故设椭圆C的方程为x‎2‎a‎2‎‎+y‎2‎b‎2‎=1(a>b>0)‎． ‎ 则由题意可得a‎2‎‎-‎b‎2‎‎=1‎‎1‎‎2‎a‎2‎‎+‎(‎‎3‎‎2‎‎)‎‎2‎b‎2‎=1‎，解得a‎2‎‎=4‎b‎2‎‎=3‎． 故椭圆C的方程为x‎2‎‎4‎‎+y‎2‎‎3‎=1‎． ‎(2)‎证明：‎∵‎直线的斜率为‎1‎‎2‎，且不过P(1,‎3‎‎2‎)‎点，‎∴‎可设直线l：y=‎1‎‎2‎x+m(m≠1)‎． 联立方程组x‎2‎‎4‎‎+y‎2‎‎3‎=1‎y=‎1‎‎2‎x+m，消y得x‎2‎‎+mx+m‎2‎-3=0.‎又设A(x‎1‎,y‎1‎)‎，B(x‎2‎,y‎2‎)‎， 故有‎△=m‎2‎-4(m‎2‎-3)>0‎x‎1‎‎+x‎2‎=-mx‎1‎x‎2‎‎=m‎2‎-3‎， 所以k‎1‎‎+k‎2‎=y‎1‎‎-‎‎3‎‎2‎x‎1‎‎-1‎+y‎2‎‎-‎‎3‎‎2‎x‎2‎‎-1‎=‎‎(y‎1‎-‎3‎‎2‎)(x‎2‎-1)+(y‎2‎-‎3‎‎2‎)(x‎1‎-1)‎‎(x‎1‎-1)(x‎2‎-1)‎ ‎=‎(‎1‎‎2‎x‎1‎+m-‎3‎‎2‎)(x‎2‎-1)+(‎1‎‎2‎x‎2‎+m-‎3‎‎2‎)(x‎1‎-1)‎‎(x‎1‎-1)(x‎2‎-1)‎ ‎‎=x‎1‎x‎2‎‎+(m-2)(x‎1‎+x‎2‎)-2m+3‎x‎1‎x‎2‎‎-(x‎1‎+x‎2‎)+1‎ ‎‎=m‎2‎‎-3+(m-2)(-m)-2m+3‎m‎2‎‎-3-(-m)+1‎=0‎，所以k‎1‎‎+‎k‎2‎为定值0。‎