【数学】2018届一轮复习北师大版不等式选讲第一节绝对值不等式教案
第一节 绝对值不等式
☆☆☆2017考纲考题考情☆☆☆
考纲要求
真题举例
命题角度
1.理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式:
①|a+b|≤|a|+|b|;
②|a-b|≤|a-c|+|c-b|;
2.会利用绝对值的几何意义求解以下类型的不等式:
|ax+b|≤c;|ax+b|≥c;
|x-a|+|x-b|≥c。
2016,全国卷Ⅰ,24,10分(绝对值不等式的求解)
2016,全国卷Ⅲ,24,10分(绝对值不等式的求解)
2015,全国卷Ⅰ,24,10分(绝对值不等式的求解,分段函数的图象)
本部分在高考中的考查主要侧重于两个方面:一是考查绝对值不等式的解法,往往含有两个绝对值号;另一方面是利用不等式的解集或利用函数的最值求不等式中所含的参数的取值范围。
微知识 小题练
自|主|排|查
1.绝对值三角不等式
定理1:如果a,b是实数,那么|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立。
定理2:如果a,b,c是实数,那么|a-b|≤|a-c|+|c-b|,当且仅当(a-c)(c-b)≥0时,等号成立。
2.绝对值不等式的解法
(1)含绝对值的不等式|x|<a与|x|>a的解集:
不等式
a>0
a=0
a<0
|x|<a
{x|-a<x<a}
∅
∅
|x|>a
{x|x>a或x<-a}
{x|x∈R且x≠0}
R
(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法:
①|ax+b|≤c⇔-c≤ax+b≤c;
②|ax+b|≥c⇔ax+b≥c或ax+b≤-c。
微点提醒
1.应用“零点分区法”的注意点
令每个绝对值符号里的代数式等于零,求出相应的根,要把这些根按由小到大进行排序,在各个区间上解不等式时,端点值要不重不漏。
2.从解集理解不等式恒成立问题
不等式的解集为R说明不等式恒成立,不等式的解集为∅,说明其对立面恒成立。
小|题|快|练
1.设ab<0,a,b∈R,那么正确的是( )
A.|a+b|>|a-b|
B.|a-b|<|a|+|b|
C.|a+b|<|a-b|
D.|a-b|<||a|-|b||
【解析】 解法一:特殊值法。
取a=1,b=-2,则满足ab=-2<0,
这样有|a+b|=|1-2|=1,
|a-b|=|1-(-2)|=3,
|a|+|b|=1+2=3,
||a|-|b||=|1-2|=1,
∴只有选项C成立,而A、B、D都不成立。故选C。
解法二:由ab<0得a,b异号,
易知|a+b|<|a-b|,|a-b|=|a|+|b|,|a-b|>||a|-|b||,
∴选项C成立,A、B、D均不成立。故选C。
【答案】 C
2.若关于x的不等式|x-a|<1的解集为(1,3),则实数a的值为________。
【解析】 由|x-a|<1,则-1
k的解集为R,则实数k的取值范围为________。
【解析】 ∵||x+1|-|x-2||≤3,
∴-3≤|x+1|-|x-2|≤3,
∴k<(|x+1|-|x-2|)的最小值,
即k<-3。
【答案】 (-∞,-3)
5.若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为________。
【解析】 |x-2y+1|=|(x-1)-2(y-2)-2|≤|x-1|+2|y-2|+2≤5。
【答案】 5
微考点 大课堂
考点一
含绝对值的不等式的解法
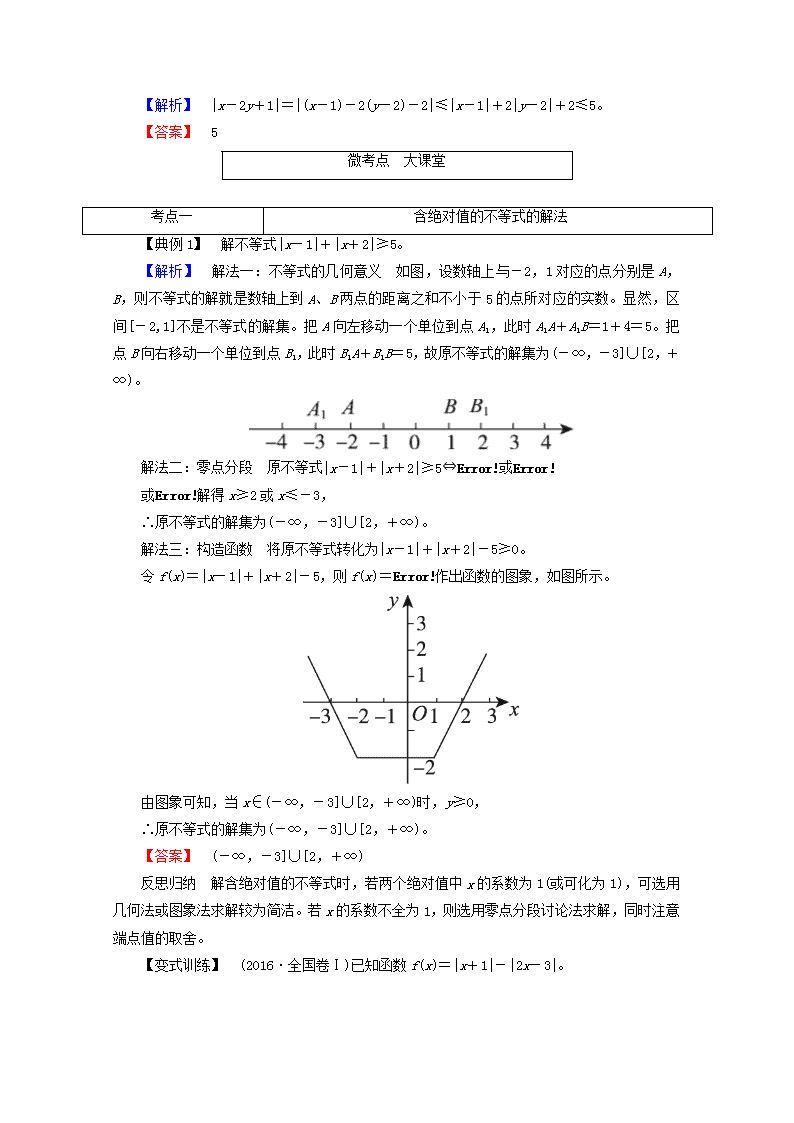
【典例1】 解不等式|x-1|+|x+2|≥5。
【解析】 解法一:不等式的几何意义 如图,设数轴上与-2,1对应的点分别是A,B,则不等式的解就是数轴上到A、B两点的距离之和不小于5的点所对应的实数。显然,区间[-2,1]不是不等式的解集。把A向左移动一个单位到点A1,此时A1A+A1B=1+4=5。把点B向右移动一个单位到点B1,此时B1A+B1B=5,故原不等式的解集为(-∞,-3]∪[2,+∞)。
解法二:零点分段 原不等式|x-1|+|x+2|≥5⇔或
或解得x≥2或x≤-3,
∴原不等式的解集为(-∞,-3]∪[2,+∞)。
解法三:构造函数 将原不等式转化为|x-1|+|x+2|-5≥0。
令f(x)=|x-1|+|x+2|-5,则f(x)=作出函数的图象,如图所示。
由图象可知,当x∈(-∞,-3]∪[2,+∞)时,y≥0,
∴原不等式的解集为(-∞,-3]∪[2,+∞)。
【答案】 (-∞,-3]∪[2,+∞)
反思归纳 解含绝对值的不等式时,若两个绝对值中x的系数为1(或可化为1),可选用几何法或图象法求解较为简洁。若x的系数不全为1,则选用零点分段讨论法求解,同时注意端点值的取舍。
【变式训练】 (2016·全国卷Ⅰ)已知函数f(x)=|x+1|-|2x-3|。
(1)画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集。
【解析】 (1)f(x)=
y=f(x)的图象如图所示。
(2)由f(x)的表达式及图象知,当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=或x=5。
故f(x)>1的解集为{x|15}。
所以|f(x)|>1的解集为{x|x<或15}。
【答案】 (1)见解析 (2){x|x<或15}
考点二
含绝对值的不等式的证明
【典例2】 设不等式-2<|x-1|-|x+2|<0的解集为M,a,b∈M。
(1)证明:<;
(2)比较|1-4ab|与2|a-b|的大小,并说明理由。
【解析】 (1)证明:记f(x)=|x-1|-|x+2|=
由-2<-2x-1<0,解得-0,
所以|1-4ab|2>4|a-b|2,
故|1-4ab|>2|a-b|。
【答案】 (1)见解析 (2)|1-4ab|>2|a-b|
反思归纳 1.利用绝对值的定义去掉绝对值符号,转化为普通不等式再证明。
2.利用三角不等式||a|-|b||≤|a±b|≤|a|+|b|进行证明。
3.转化为函数问题,数形结合进行证明。
【变式训练】 已知x,y∈R,且|x+y|≤,|x-y|≤,求证:|x+5y|≤1。
【证明】 ∵|x+5y|=|3(x+y)-2(x-y)|。
∴由绝对值不等式的性质,得
|x+5y|=|3(x+y)-2(x-y)|≤
|3(x+y)|+|2(x-y)|=3|x+y|+2|x-y|≤3×+2×=1。
即|x+5y|≤1。
考点三
含绝对值的不等式的综合应用
【典例3】 (2016·全国卷Ⅲ)已知函数f(x)=|2x-a|+a。
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x-1|。当x∈R时,f(x)+g(x)≥3,求a的取值范围。
【解析】 (1)当a=2时,f(x)=|2x-2|+2。
解不等式|2x-2|+2≤6得-1≤x≤3。
因此f(x)≤6的解集为{x|-1≤x≤3}。
(2)当x∈R时,
f(x)+g(x)=|2x-a|+a+|1-2x|
≥|2x-a+1-2x|+a
=|1-a|+a。
所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3。①
当a≤1时,①等价于1-a+a≥3,无解。
当a>1时,①等价于a-1+a≥3,解得a≥2。
所以a的取值范围是[2,+∞)。
【答案】 (1){x|-1≤x≤3} (2)[2,+∞)
反思归纳 1.不等式恒成立问题的解法
若不等式f(x)≤a在区间D上恒成立,则f(x)max≤a;若f(x)≥a在区间D上恒成立,则f(x)min≥a。
2.不等式能成立问题的解法
若f(x)≤a在区间D上能成立,则f(x)min≤a,若f(x)≥a在区间D上能成立,则f(x)max≥a。
【变式训练】 (1)(2016·重庆模拟)已知函数f(x)=|2x+1|,g(x)=|ax|。
①当a=1时,解不等式f(x)≥g(x)+1;
②当a=2时,若对一切x∈R,恒有f(x)+g(x)≥b成立,求实数b的取值范围。
(2)已知函数f(x)=|x+3|-|x-2|。
①求不等式f(x)≥3的解集;
②若f(x)≥|a-4|有解,求a的取值范围。
【解析】 (1)①f(x)≥g(x)+1⇔|2x+1|≥|x|+1,当x≤-时,不等式⇔-(2x+1)≥-x+1,解得x≤-2;
当-a对于一切x∈R恒成立,求实数a的取值范围。
解析 由绝对值的几何意义知:|x-4|+|x+5|≥9,则log3(|x-4|+|x+5|)≥2,所以要使不等式log3(|x-4|+|x-5|)>a对于一切x∈R恒成立,则需a<2。
答案 a<2
3.对于任意实数a,b已知|a-b|≤1,|2a-1|≤1,且恒有|4a-3b+2|≤m,求实数m的取值范围。
解析 因为|a-b|≤1,|2a-1|≤1,
所以|3a-3b|≤3,≤,
所以|4a-3b+2|=
≤|3a-3b|++≤3++=6,
即|4a-3b+2|的最大值为6,
所以m≥6。
答案 m≥6