2018-2019学年安徽省阜阳市第三中学高二竞培中心下学期第二次调研考试数学（文）试题 Word版

2018-2019学年安徽省阜阳市第三中学高二竞培中心下学期第二次调研考试数学（文）试题 Word版

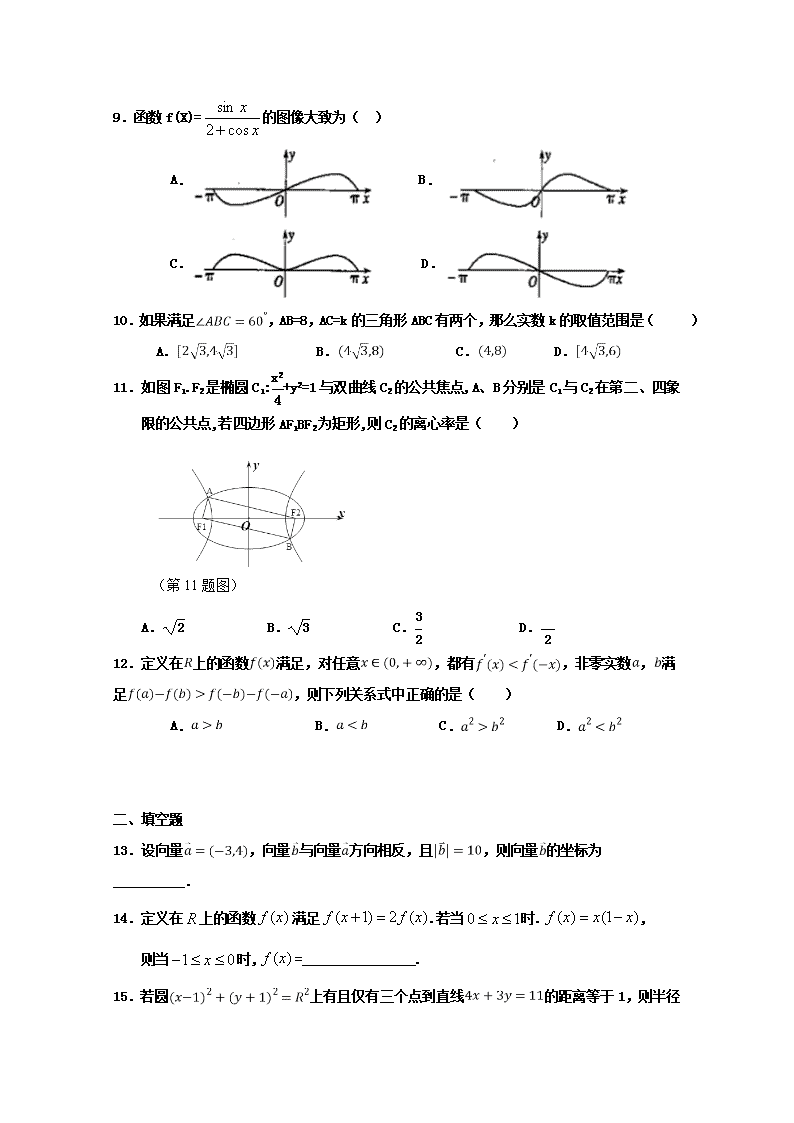
阜阳三中2018—2019学年第二学期竞培中心二调考试 数 学 试 卷 考试时间：120分钟 满分：150分 ‎ 一、单选题 ‎1．已知，，则的元素个数为（ ）‎ A．1 B．2 C．3 D．4‎ ‎2．若幂函数的图象过点，则函数的最大值为（ ）‎ A．1 B． C．2 D．‎ ‎3．已知实数、满足约束条件，则目标函数的最小值为( ) A． B． C． D．‎ ‎4．在正方体中，E、F分别是AB、的中点，则异面直线、FC所成角的余弦值为（ ）‎ A． B． C． D．‎ ‎5．在边长为1的等边三角形ABC中，点P是边AB上一点，且BP＝2PA，则（ ） ‎ ‎ A． B． C． D．1‎ ‎6．已知等差数列，，前项和为，，则（ ）‎ A．0 B．1 C．2018 D．2019‎ ‎7．若，则（　　）‎ A． B． C． D．‎ ‎8．已知函数，若对任意的正数，满足，则的最小值为（ ）‎ A．6 B．8 C．12 D．24‎ ‎9．函数f(X)=的图像大致为（ ）‎ A． B．‎ C． D．‎ ‎10．如果满足，AB=8，AC=k的三角形ABC有两个，那么实数k的取值范围是（ ） A． B． C． D．‎ ‎11．如图F1.F2是椭圆C1:+y2=1与双曲线C2的公共焦点,A、B分别是C1与C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是（　　）‎ ‎（第11题图）‎ ‎ ‎ A． B． C． D． ‎12．定义在上的函数满足，对任意，都有，非零实数，满足，则下列关系式中正确的是（ ）‎ A． B． C． D．‎ 二、填空题 ‎13．设向量，向量与向量方向相反，且，则向量的坐标为__________．‎ ‎14．定义在上的函数满足.若当时.,‎ 则当时,=________________.‎ ‎15．若圆上有且仅有三个点到直线的距离等于1，则半径 的值为______．‎ ‎16．已知正三棱锥的底面边长为3，外接球的表面积为，则正三棱锥的体积为________.‎ 三、解答题 ‎17．（本题10分）已知数列中，且（）．‎ ‎（Ⅰ）求，；并证明是等比数列；‎ ‎（Ⅱ）设，求数列的前项和．‎ ‎18．（本题12分）在中，角、、的对边分别为，，，, ‎ ‎（1）若，求的值；‎ ‎（2）求的取值范围.‎ ‎19．（本题12分）已知四棱锥中，底面，，，，.‎ ‎（1）当变化时，点到平面的距离是否为定值？若是，请求出该定值；若不是，请说明理由；‎ ‎（2）若，求直线与平面所成角的正弦值.‎ ‎20．（本题12分）国家质量监督检验检疫局于2004年5月31日发布了新的车辆驾驶人员血液、呼气酒精含量阀值与检验国家标准新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克百毫升，小于80毫克百毫升为饮酒驾车，血液中的酒精含量大于或等于80毫克百毫升为醉酒驾车某高中研究性小组经过反复试验获得，喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图：‎ 该函数近似模型如下：,又已知刚好过1小时时测得酒精含量值为毫克百毫升根据上述条件，回答以下问题：‎ 试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值？最大值是多少？‎ 试计算喝一瓶啤酒后多少小时后才可以驾车？时间以整小时计算 参考数据：，，，‎ ‎21．（本题12分）已知动圆P恒过定点，且与直线相切．‎ ‎（Ⅰ）求动圆P圆心的轨迹M的方程；‎ ‎（Ⅱ）正方形ABCD中，一条边AB在直线y＝x＋4上，另外两点C、D在轨迹M上，求正方形的面积．‎ ‎22．已知函数．‎ ‎(1)若，求的单调区间；‎ ‎(2)证明：．‎ 阜阳三中2018—2019学年第二学期竞培中心二调考试 数 学 试 卷 一、单选题 CBDDC ABCAB DD 二、填空题 ‎13． 14 15．3 16．或 三、解答题 ‎17．（本题10分）已知数列中，且（）．‎ ‎（Ⅰ）求，；并证明是等比数列；‎ ‎（Ⅱ）设，求数列的前项和．‎ ‎【答案】（Ⅰ），证明见解析；（Ⅱ）.‎ ‎（Ⅰ）由题意，可知：‎ ‎ ，‎ ‎ ．‎ ‎①当时，，‎ ‎②当时， ．‎ 数列是以为首项，为公比的等比数列．(如果没有求首相，就该说明不为零）‎ ‎（Ⅱ）由（Ⅰ），可知：‎ ‎，‎ ‎ ．．‎ ‎ ．‎ ‎ ‎ ‎， ③‎ ‎ ④‎ ‎③-④，可得：‎ ‎ ‎ ‎，‎ 分项求和也可以 ‎18．（本题12分）在中，角、、的对边分别为，，，, ‎ ‎（1）若，求的值；‎ ‎（2）求的取值范围.‎ ‎【答案】(1) (2) ‎ ‎【详解】‎ ‎（1）由 则 ‎，,所以，则 由 且 ‎ 所以，‎ 则 ‎（2）由 所以，‎ 故 令，则 ，所以 故而,,‎ 当时， 有最大值 且 所以的取值范围是 ‎19．（本题12分）已知四棱锥中，底面，，，，.‎ ‎（1）当变化时，点到平面的距离是否为定值？若是，请求出该定值；若不是，请说明理由；‎ ‎（2）若，求直线与平面所成角的正弦值.‎ ‎【答案】(1)见解析；(2) ‎ ‎【详解】‎ ‎（1）由，，知，则，‎ 由面，面得，‎ 由，，面，‎ 则面，则点到平面的距离为一个定值，.‎ ‎（2）设直线与平面所成的角为，‎ 由，可知，‎ 又面，面，故，，‎ 则面，‎ 则点到平面的距离为，‎ 由知点与点到平面的距离相等，‎ 则点到平面的距离为，‎ 由知，‎ 故.‎ ‎20．（本题12分）国家质量监督检验检疫局于2004年5月31日发布了新的车辆驾驶人员血液、呼气酒精含量阀值与检验国家标准新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克百毫升，小于80毫克百毫升为饮酒驾车，血液中的酒精含量大于或等于80毫克百毫升为醉酒驾车某高中研究性小组经过反复试验获得，喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图：‎ 该函数近似模型如下：,又已知刚好过1小时时测得酒精含量值为毫克百毫升根据上述条件，回答以下问题：‎ 试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值？最大值是多少？‎ 试计算喝一瓶啤酒后多少小时后才可以驾车？时间以整小时计算 参考数据：，，，‎ ‎【答案】（1）喝一瓶啤酒小时血液中的酒精含量达到最大值毫克百毫升；（2）需6个小时后才可以合法驾车。‎ ‎【详解】‎ 解：由图可知，当函数取得最大值时，；‎ 此时，‎ 又，‎ 所以，解得；‎ 所以，由二次函数的性质可知，‎ 当时，函数取得最大值为，‎ 故喝一瓶啤酒小时血液中的酒精含量达到最大值毫克百毫升；‎ 由题意知，当车辆驾驶人员血液中的酒精小于20毫克百毫升时可以驾车，此时；此处也可以求出函数在（0,2）上的值域再说明更好。‎ 由，得，‎ 两边取自然对数，得，‎ 即，‎ 所以；‎ 故喝啤酒后需6个小时后才可以合法驾车 ‎21．（本题12分）已知动圆P恒过定点，且与直线相切．‎ ‎（Ⅰ）求动圆P圆心的轨迹M的方程；‎ ‎（Ⅱ）正方形ABCD中，一条边AB在直线y＝x＋4上，另外两点C、D在轨迹M上，求正方形的面积．‎ ‎【答案】（1） ；（2）或 ‎【详解】‎ ‎（1）由题意得动圆的圆心到点的距离与它到直线的距离相等，‎ 所以圆心的轨迹是以为焦点，以为准线的抛物线，且，‎ 所以圆心的轨迹方程为．‎ ‎（2）由题意设边所在直线方程为，‎ 由消去整理得，‎ ‎∵直线和抛物线交于两点，‎ ‎∴，解得．‎ 设，，‎ 则.‎ ‎∴．‎ 又直线与直线间的距离为，‎ ‎∵，‎ ‎∴ ，解得或，‎ 经检验和都满足．‎ ‎∴正方形边长或，‎ ‎∴正方形的面积或．‎ ‎22．已知函数．‎ ‎(1)若，求的单调区间；‎ ‎(2)证明：．‎ ‎【答案】（1）增区间，减区间；（2）见解析 ‎【详解】‎ ‎（1）的定义域为，‎ 若，则，，‎ 令，则在上恒成立，‎ 故在上单调递增，‎ 又，‎ 故当时，；当时，‎ 即的增区间为，减区间为。‎ ‎（2），‎ 由（1）可知在上必有唯一零点，设为，则，‎ 当时，，单调递减，‎ 当时，，单调递增，‎ ‎∴，‎ 又∵，∴，另外，∴，‎ ‎∴，得证.‎