天津市第二中学2020-2021学年高二第一学期期中考试数学试卷

天津市第二中学2020-2021学年高二第一学期期中考试数学试卷

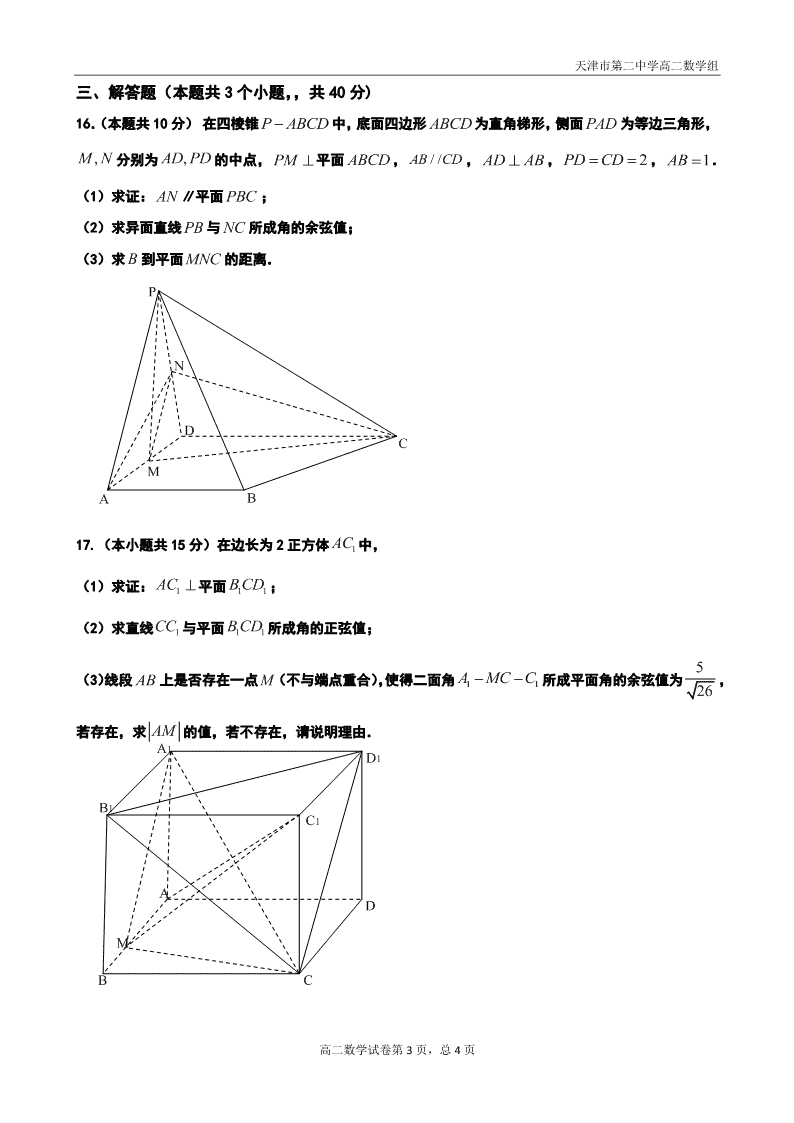
天津市第二中学高二数学组 高二数学试卷第 1 页，总 4 页 2020-2021 学年度天津二中第一学期期中考试 高二数学 一、选择题（本题共 10 小题，每题 4 分，共 40 分) 1．直线3 3 2 0xy   的倾斜角是（ ） A． 6  B． 3  C． 2 3  D． 5 6  2．圆 222 2 1x y x y    的圆心和半径分别是（ ） A．  1, 1 ；1 B． 1, 1 ； 3 C． 1,1 ；1 D． 1,1 ； 3 3．直线 2 3 0xy   与圆 C： 22( 1) 1xy   的位置关系是（ ） A．相交 B．相切 C．相离 D．不确定 4．椭圆 2221xy的离心率为（ ） A． 1 2 B． 2 2 C． 2 D．2 5．已知直线  1 : 2 5 8 0l x a y    ，  2 : 3 4 3 5 0l a x y a     平行，则实数 a 的值为（ ） A．-1 或-7 B．-7 C．-1 D． 13 3 6．直线 0xy被圆 226 2 4 0x y x y     截得的弦长等于（ ） A．4 B．2 C． 22 D． 2 7．命题 p：“35m”是命题 q：“曲线 22 135 xy mm 表示椭圆”的（ ） A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分也不必要条件 8．若直线l 的方向向量为  1, 3a  ，则直线 的斜率为（ ） A． 1 2 B． 3 2 C． 3 3 D． 3 9．过点 (1,0)P 作圆 22( 2) ( 2) 1xy    的切线，则切线方程为（ ） A． 1x  或3 4 3 0xy   B． 或3 4 3 0xy   C． 1y  或 4 3 4 0xy   D． 或 天津市第二中学高二数学组 高二数学试卷第 2 页，总 4 页 10. 唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一 个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再 回军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为 221xy，若将军从点  1, 2P  处出发，河岸线所在直线方程为 35xy，并假定将军只要到达军营所在区域即回到军营，则 “将军饮马回营”的最短总路程为（ ） A．4 B．5 C． 3 10 2 D． 51 二、填空题（本题共 5 个小题，每题 4 分，共 20 分) 11．椭圆 22 143 xy的通径长为 ． 12．两圆 2240xy   与 226 8 6 0x y x y     的公共弦长为 ． 13．已知圆 22( 4) ( 5) 169xy    ，过点 1,1 的直线交圆于 ,AB两点，则 AB 的取值范围为 ． 14．如图，过椭圆 22 22:1xyE ab 0ab 的左焦点 1F 作直线l 交椭圆 E 于 ,AB两点，O 为坐标原点， 连接 BO 并延长交椭圆 于C 点，若 1CF AB ，且 113CF AF ，则该椭圆 E 的离心率 e 为 ． 15．已知 1F ， 2F 分别为椭圆   22 2210xy abab    的左、右焦点， P 为椭圆上任意一点， M 为 2PF 上 的三等分点，且满足 2 2MF PM ，若 1OP MF ，则该椭圆的离心率 的取值范围是 ． y x P M O F2 F1 A B F1 O C x y 天津市第二中学高二数学组 高二数学试卷第 3 页，总 4 页 三、解答题（本题共 3 个小题，，共 40 分) 16．（本题共 10 分） 在四棱锥 P ABCD 中，底面四边形 ABCD为直角梯形，侧面 PAD 为等边三角形， ,MN分别为 ,AD PD 的中点， PM 平面 ， //AB CD ， AD AB ， 2PD CD， 1AB  ． （1）求证： AN ∥平面 PBC ； （2）求异面直线 PB 与 NC 所成角的余弦值； （3）求 B 到平面 MNC 的距离． 17.（本小题共 15 分）在边长为 2 正方体 1AC 中， （1）求证： 1AC 平面 11B CD ； （2）求直线 1CC 与平面 11B CD 所成角的正弦值； （3）线段 AB 上是否存在一点 M（不与端点重合），使得二面角 11A MC C所成平面角的余弦值为 5 26 ， 若存在，求 AM 的值，若不存在，请说明理由． N D C A P B M A1 C1 A B M D1 C D B1 天津市第二中学高二数学组 高二数学试卷第 4 页，总 4 页 18.（本小题共 15 分） 已知椭圆 E ： 22 221( 0)xy abab    ， 21,F F 分别为左右焦点，O 为坐标原点， 过 作直线 1l 交椭圆于 ,AB两点，若 1ABF 周长的最小值为 2( 2 1) ，面积的最大值为1， （1）求椭圆 E 的标准方程； （2）设直线 2 :l y kx m ， ( 0)m  交椭圆 E 于 M ， N 两点， （i）若 2 2k  ，且 MON 的面积为 2 2 ，求 m 的值； （ii）若 x 轴上任意一点到直线 2MF 与 2NF 的距离均相等，求证：直线 2l 恒过一定点，并求出该定点的坐 标． N y M B A F2 F1 x O