2019届二轮复习作图法第2课课件（9张）（全国通用）

2019届二轮复习作图法第2课课件（9张）（全国通用）

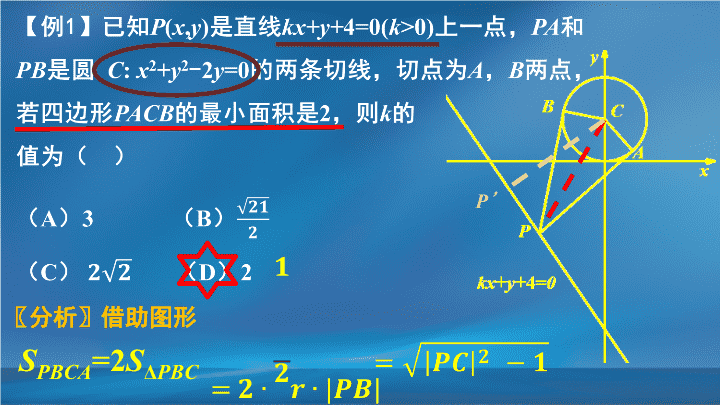
第二讲 解析几何问题 【例 1 】 已知 P ( x , y ) 是 直线 kx+y+ 4=0( k >0) 上 一点， PA 和 PB 是圆 C : x 2 + y 2 - 2 y =0 的 两条切线，切点为 A ， B 两点，若四边形 PACB 的最小面积是 2 ，则 k 的 值 为（ ） （ A ） 3 （ B ） （ C ） （ D ） 2 〖 分析 〗 借助图形 P ’ S PBCA =2 S Δ PBC 方法点睛 直线与圆中的最值问题： 一是求参量的取值（范围） 策略一：根据几何特征构建关于参量的等式、不等式或函数求解； 二是长度或面积等几何要素的最值 策略二：根据圆的几何性质，及直线与圆的位置关系，借助图形分析取得最值时的位置 . 【 练习 】 已知 Q 为圆 C ： ( x - 3) 2 + y 2 =1 上一动点，则点 Q 到直线 y = x +1 距离的最小值 是 _____ ； A (0,1 ) ， B (2,3) 为直线 y = x +1 上两点 , S Δ QAB 的最小值 是 ____ ；由直线 y = x +1 上 一动点 P 向圆 C 引切线，则切线长的最小值 是 _____ ；已知 P 为直线 y=x +1 上一动点，过 P 作圆 C 的切线 PA ， PB 其中， A 、 B 为切点，则当线段 PC 长 是 __ 时 ， ∠ APB 最大；过点 (1 , ) 的 直线 l 将 圆 C 分成两 段弧，当劣弧所对的圆心角最小时， 直线 l 的斜率是 ____ ； 当直线 l 截 得的弦最短（或最长 ）时 ， 直线 l 的 方程是 _______ . 【例 2】 一动圆 P 与圆 C 1 :( x - 1) 2 + y 2 =1 外切 ，同时与 圆 C 2 :( x + 1) 2 + y 2 =9 内切 ，则动圆 P 的轨迹方程是 _____ ；若点 M 是圆 C 3 : x 2 +( y - 3) 2 =1 上 的动 点，点 F (1,0) ， 则当 P 的坐标为 _______ 时 ， | PM |+ | PF | 的 最大值是 _______. 〖 分析 〗 设 P ( x,y ) 圆 P 的半径 r =| PF | - 1=3 - | PC 2 | | PC 2 | + | PF |=4 所以 P 的轨迹为 椭圆，方程为 【例 2】 若 点 M 是圆 C 3 : x 2 +( y - 3) 2 =1 上 的动 点，点 F (1,0) ， 则当 P 的坐标为 _______ 时 ， | PM |+| PF | 的 最大值是 _______. 〖 分析 〗 | PM |+| PF |=4+ | PM | - | PC 2 | ≤ 4+| MC 2 | P ’ M ∴ ( | PM |+| PF |) max =| C 2 C 3 |+1=5+ 此时 方法点睛 解决平面向量问题的技巧： 将 题目的“数”与“形”相结合，将题目所给条件 一一对应做出图形来 帮助解题 ，既能 减少解题时间，也不会漏掉题目条件 ，从而提高 答题效率。 【 练习 】 1. 抛物线 y 2 =4 x 的焦点为 F ，点 P ( x , y ) 为该抛物线上的动点，又点 A( - 1 , 0) ，则 的最小值是（ ） A . B. C. D. 2. （ 17 年·东城一模理 13 ）双曲线 ( a >0, b >0) 的渐近线为等边三角形 OAB 的边 OA , OB 所在直线，直线 AB 过双曲线的焦点，且 | AB |=2 ，则 a = _______ ． 3. 在直角坐标系 xOy ，直线 l 过 抛物线 y 2 =4 x 的 焦点 F ，且与该抛物线相交于 A,B 两点，其中点 A 在 x 轴上方．若直线 l 的倾斜角为 60 ° ，则 |OA|= ． 同学们，再见！