湖南省2019届高三六校联考试题（4月）数学（理）(1)

湖南省2019届高三六校联考试题（4月）数学（理）(1)

绝密★启用前 湖南省2019届高三六校联考试题 考生注意：‎ ‎1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。时量120分钟，满分150分。答题前，考生务必将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。‎ ‎2．作答选择题，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。作答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ ‎3．考试结束时，监考员将题卷、答题卡一并收回。‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。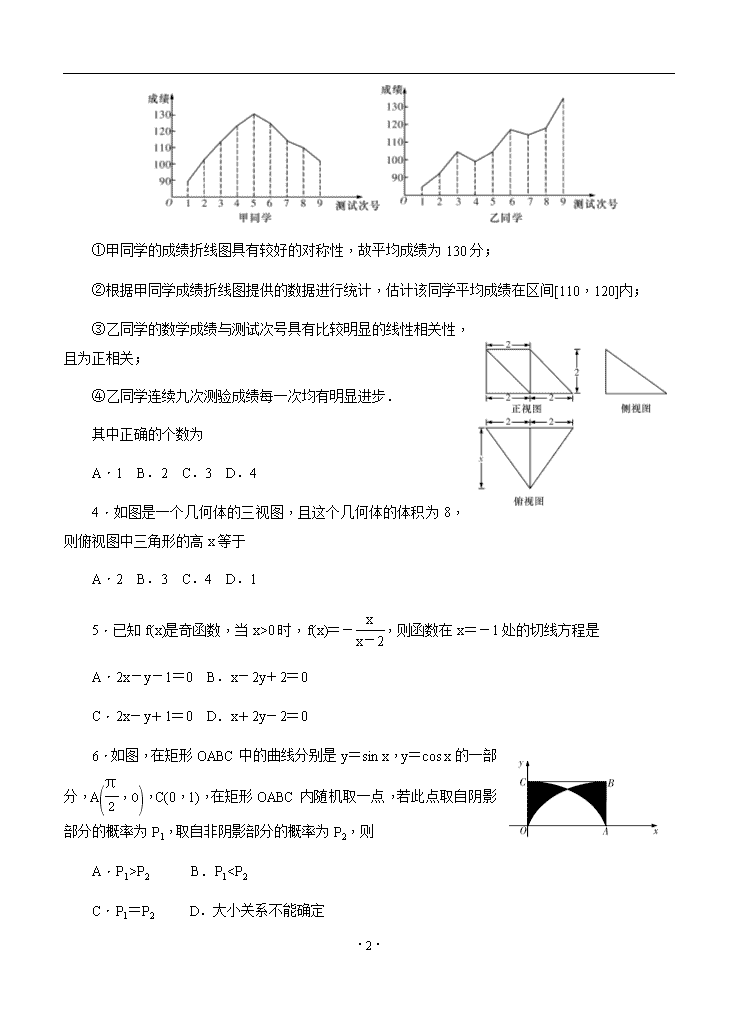‎ ‎1．复数z满足(1＋i)z＝，则z＝‎ A．2＋2i B．1＋2i C．1－2i D．2－2i ‎2．已知集合A＝，则∁RA＝‎ A．[－3，1) B．(－∞，－3)∪[1，＋∞)‎ C．(－3，1) D．(－∞，－3]∪(1，＋∞)‎ ‎3．对某两名高三学生在连续9次数学测试中的成绩(单位：分)进行统计得到如下折线图，下面是关于这两位同学的数学成绩分析．‎ ‎·19·‎ ‎①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分；‎ ‎②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内；‎ ‎③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关；‎ ‎④乙同学连续九次测验成绩每一次均有明显进步．‎ 其中正确的个数为 A．1 B．2 C．3 D．4‎ ‎4．如图是一个几何体的三视图，且这个几何体的体积为8，则俯视图中三角形的高x等于 A．2 B．3 C．4 D．1‎ ‎5．已知f(x)是奇函数，当x>0时，f(x)＝－，则函数在x＝－1处的切线方程是 A．2x－y－1＝0 B．x－2y＋2＝0‎ C．2x－y＋1＝0 D．x＋2y－2＝0‎ ‎6．如图，在矩形OABC中的曲线分别是y＝sin x，y＝cos x的一部分，A，C(0，1)，在矩形OABC内随机取一点，若此点取自阴影部分的概率为P1，取自非阴影部分的概率为P2，则 A．P1>P2 B．P10，b>0)，以点P(b，0)为圆心，a为半径作圆P，圆P与双曲线C的一条渐近线交于M，N两点，若∠MPN＝90°，则C的离心率为 A. B. C. D. ‎9．若m，n均为非负整数，在做m＋n的加法时各位均不进位(例如：2019＋100＝2119，则称(m，n)为“简单的”有序对，而m＋n称为有序对(m，n)的值，那么值为2019的“简单的”有序对的个数是 A．30 B．60 C．96 D．100‎ ‎10．若x1是方程xex＝1的解，x2是方程xln x＝1的解，则x1x2等于 A．e B．1 C. D．－1‎ ‎11．已知函数f(x)＝sin(ωx＋φ)的部分图象如图所示，且f(x)在上恰有一个最大值和一个最小值(其中最大值为1，最小值为－1)，则ω的取值范围是 A. B. C. D. ‎12．已知函数f(x)＝ex－ax－1在区间内存在极值点，且f(x)<0恰好有唯一整数解，则a的取值范围是(其中e为自然对数的底数，e＝2.71828…)‎ A. B.∪ C.∪ D．(e－1，e)‎ ‎·19·‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎13．已知二项式的展开式中的常数项为－160，则a＝________．‎ ‎14．若实数x，y满足不等式组则目标函数z＝3x－y的最大值为________．‎ ‎15．在《九章算术》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马．如图，若四棱锥P－ABCD为阳马，侧棱PA⊥底面ABCD，且PA＝3，BC＝AB＝4，设该阳马的外接球半径为R，内切球半径为r，则＝________．‎ ‎16．在△ABC中，a，b，c分别为角A，B，C所对的边，若c＝2b，△ABC的面积为1，则a的最小值为________．‎ 三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤。第17－21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题，共60分。‎ ‎17．(本小题满分12分)‎ 已知数列{an}中，a1＝1，Sn是数列{an}的前n项和，且对任意的r、t∈N*，都有＝.‎ ‎(Ⅰ)判断{an}是否为等差数列，并证明你的结论；‎ ‎(Ⅱ)若数列{bn}满足＝2n－1(n∈N*)，设Tn是数列{bn}的前n项和，证明：Tn<6.‎ ‎18．(本小题满分12分)‎ 在Rt△ABC中，∠ABC＝90°，tan∠ACB＝.已知E，F分别是BC，AC的中点．将△‎ ‎·19·‎ CEF沿EF折起，使C到C′的位置且二面角C′－EF－B的大小是60°.连接C′B，C′A，如图：‎ ‎(Ⅰ)求证：平面C′FA⊥平面ABC′；‎ ‎(Ⅱ)求平面AFC′与平面BEC′所成二面角的大小．‎ ‎19．(本小题满分12分)‎ 已知平面上一动点P到定点F(，0)的距离与它到直线x＝的距离之比为，记动点P的轨迹为曲线C.‎ ‎(Ⅰ)求曲线C的方程；‎ ‎(Ⅱ)设直线l：y＝kx＋m与曲线C交于M，N两点，点M在x轴上的射影为G，O为坐标原点，若4·＝9·，求△MON面积的最大值．‎ ‎20．(本小题满分12分)‎ 随着食品安全问题逐渐引起人们的重视，有机、健康的高端绿色蔬菜越来越受到消费者的欢迎，同时生产－运输－销售一体化的直销供应模式，不仅减少了成本，而且减去了蔬菜的二次污染等问题．‎ ‎(Ⅰ)在有机蔬菜的种植过程中，有机肥料使用是必不可少的．根据统计某种有机蔬菜的产量与有机肥料的用量有关系，每个有机蔬菜大棚产量的增加量y(百斤)与使用堆沤肥料x(千克)之间对应数据如下表：‎ 使用堆沤肥料x (千克)‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 产量增加量y(百斤)‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ 依据表中的数据，用最小二乘法求出y关于x的线性回归方程＝x＋；并根据所求线性回归方程，估计如果每个有机蔬菜大棚使用堆沤肥料10千克，则每个有机蔬菜大棚产量增加量y是多少百斤？‎ ‎·19·‎ ‎(Ⅱ)某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装，以每份10元的价格销售到生鲜超市．“乐购”生鲜超市以每份15元的价格卖给顾客，如果当天前8小时卖不完，则超市通过促销以每份5元的价格卖给顾客(根据经验，当天能够把剩余的有机蔬菜都低价处理完毕，且处理完毕后，当天不再进货)．该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量(单位：份)，制成如下表格 (注：x，y∈N*，且x＋y＝30)：‎ 每日前8个小时 销售量(单位：份)‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ 频数 ‎10‎ x ‎16‎ ‎16‎ ‎15‎ ‎13‎ y 若以100天记录的频率作为每日前8小时销售量发生的概率，该生鲜超市当天销售有机蔬菜利润的期望值为决策依据，当购进17份比购进18份的利润的期望值大时，求x的取值范围．‎ 附：回归方程系数公式＝，＝－·.‎ ‎21．(本小题满分12分)‎ 已知f(x－1)＝2ln(x－1)－＋k(x>1)．‎ ‎(Ⅰ)判断当－1≤k≤0时f(x)的单调性；‎ ‎(Ⅱ)若x1，x2(x1≠x2)为f(x)两个极值点，求证：x[f(x1)＋f(x2)]≥(x＋1)[f(x)＋2－2x]．‎ ‎(二)选考题：共10分。请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分。‎ ‎22．(本小题满分10分)选修4—4：坐标系与参数方程 ‎·19·‎ 在平面直角坐标系xOy中，直线l的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2＝.‎ ‎(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程；‎ ‎(Ⅱ)设P为曲线C上的点，PQ⊥l，垂足为Q，若的最小值为2，求m的值．‎ ‎23．(本小题满分10分)选修4—5：不等式选讲 已知函数f(x)＝|x－2a|－|x－a|，a∈R.‎ ‎(Ⅰ)若f(1)>1，求a的取值范围；‎ ‎(Ⅱ)若a<0，对x，y∈(－∞，a]，都有不等式f(x)≤＋|y－a|恒成立，求a的取值范围．‎ 湖南省2019届高三六校联考试题 数学(理科)参考答案 一、选择题 题　号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎·19·‎ 答　案 D B B C C A A C B B D C ‎1.D　【解析】(1＋i)z＝4，z＝＝2－2i.‎ ‎2．B　【解析】∵(x＋3)(x－1)≤0且x≠1，∴A＝，∴∁RA＝(－∞，－3)∪[1，＋∞)．‎ ‎3．B　【解析】①甲同学的成绩折线图具有较好的对称性，最高130分，平均成绩为低于130分，①错误；②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内，②正确；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关，③正确；④乙同学在这连续九次测验中第四次、第七次成绩较上一次成绩有退步，故④不正确．故选B.‎ ‎4．C　【解析】该几何体为四棱锥，体积为 V＝·x＝8，‎ ‎∴x＝4.‎ ‎5．C　【解析】当x<0时，－x>0，∴f(－x)＝－，∴f(x)＝(x<0)，‎ k＝f′(－1)＝2，切点为(－1，－1)，∴切线方程为y＋1＝2(x＋1)．‎ ‎∴切线方程为2x－y＋1＝0.‎ ‎6．A　【解析】根据题意，阴影部分的面积的一半为 ‎∫0(cos x－sin x)dx＝－1，‎ ‎·19·‎ 于是此点取自阴影部分的概率为P1＝2×＝>＝.‎ 又P2＝1－P1<，故P1>P2.‎ ‎7．A　【解析】＝－，∵⊥，‎ ‎∴(λ＋μ)·(－＋)＝0，‎ ‎∴－λ2＋μ2＋(λ－μ)·＝0，∴λ＝6μ，∴＝6.‎ ‎8．C　【解析】不妨设双曲线C的一条渐近线bx－ay＝0与圆P交于M，N，因为∠MPN＝90°，所以圆心P到bx－ay＝0的距离为＝＝a，即2c2－2a2＝ac，解得e＝.故选C.‎ ‎9．B　【解析】值为2019的“简单的”有序对的个数是3×1×2×10＝60.故选B.‎ ‎10．B　【解析】考虑到x1，x2是函数y＝ex、函数y＝ln x与函数y＝的图象的公共点A，B的横坐标，而A，B两点关于y＝x对称，因此x1x2＝1.‎ ‎11．D　【解析】由题意知，f(x)＝sin(ωx＋φ)，∵f(0)＝，φ∈，∴φ＝，‎ ‎∵x∈[0，2π]，∴≤ωx＋≤2πω＋，∴≤2πω＋<，‎ ‎∴≤ω<.‎ ‎12．C　【解析】由题意得，f′(x)＝ex－a＝0在上有解，∵f′(x)在上单调递增，∴0，‎ 化简得m2<4k2＋1，　①‎ x1＋x2＝－，x1x2＝，‎ y1y2＝＝k2x1x2＋km＋m2，‎ 若4·＝9·，则4x1x2＋4y1y2＝9x1x2，即4y1y2＝5x1x2，6分 ‎∴4k2x1x2＋4km＋4m2＝5x1x2，‎ ‎∴·＋4km＋4m2＝0，‎ 即－8k2m2＋m2＝0，‎ 化简得m2＋k2＝，　②8分 ＝＝ ‎＝＝，‎ ‎·19·‎ ‎∵原点O到直线l的距离d＝，‎ ‎∴S△MON＝·d＝.10分 设4k2＋1＝t，由①②得0≤m2<，，求得x>24，‎ 故求得x的取值范围是，x∈N*.12分 ‎21．【解析】(Ⅰ)因为 f(x－1)＝2ln(x－1)＋(x>1)，‎ 所以f(x)＝2ln x＋(x>0)．‎ f′(x)＝＋＝， 2分 当－1≤k≤0时，Δ＝(4＋k)2－16＝k(k＋8)≤0，2x2＋(4＋k)x＋2>0恒成立．‎ 于是，f(x)在定义域上为单调增函数.5分 ‎(Ⅱ)证明：∵f′(x)＝＋＝， ‎ 由题设知，f′(x)＝0有两个不相等的正实数根x1，x2，则 k<－8，7分 而f(x1)＋f(x2)＝2ln x1＋＋2ln x2＋ ‎·19·‎ ‎＝2ln(x1x2)＋k ‎＝2ln(x1x2)＋k·＝k，9分 又＝k，‎ 故欲证原不等式等价于证明不等式：‎ ≥[f(x)－2(x－1)]，10分 也就是要证明：对任意x>0，有ln x≤x－1.11分 令g(x)＝ln x－x＋1(x>0)，由于g(1)＝0，并且g′(x)＝－1，‎ 当x>1时，g′(x)<0，则g(x)在(1，＋∞)上为减函数；‎ 当00，则g(x)在(0，1)上为增函数．‎ 则g(x)在(0，＋∞)上有最大值g(1)＝0，即g(x)≤0，故原不等式成立.12分 ‎22．【解析】(Ⅰ)因为曲线C的极坐标方程为ρ2＝，‎ 即ρ2＋ρ2sin2θ＝4，‎ 将ρ2＝x2＋y2，ρsin θ＝y代入上式并化简得＋＝1，3分 所以曲线C的直角坐标方程为＋＝1，‎ 直线l的普通方程为x－y－m＝0.5分 ‎(Ⅱ)设P(2cos θ，sin θ)，由点到直线的距离公式得 ＝＝，7分 ‎·19·‎ 由题意知m≠0，‎ 当m>0时，＝＝2，得m＝2＋2；‎ 当m<0时，＝＝2，得m＝－2－2；‎ 所以m＝2＋2或m＝－2－2.10分 ‎23．【解析】(Ⅰ)f(1)＝|1－2a|－|1－a|>1.1分 若a≤，则1－2a－1＋a>1，得a<－1；2分 若1，得a>1，即不等式无解； 3分 若a≥1，则2a－1＋1－a>1，得a>1, 4分 综上所述，a的取值范围是(－∞，－1)∪(1，＋∞).5分 ‎(Ⅱ)由题意知，要使得不等式恒成立，只需[f(x)]max≤[|y＋2020|＋|y－a|]min，6分 当x∈(－∞，a]时，|x－2a|－|x－a|≤－a，[f(x)]max＝－a，7分 因为|y＋2020|＋|y－a|≥|a＋2020|，‎ 所以当(y＋2020)(y－a)≤0时，[|y＋2020|＋|y－a|]min＝|a＋2020|，9分 即－a≤|a＋2020|，解得a≥－1010，结合a<0，‎ 所以a的取值范围是.10分 欢迎访问“高中试卷网”——http://sj.fjjy.org ‎·19·‎