高中数学好题经典-有难度
1;设函数 的图象在点 处的切线的斜率为
,且函数 为偶函数.若函数 满足下列条件:① ;②对一切实
数 ,不等式 恒成立.
(Ⅰ)求函数 的表达式;
(Ⅱ)求证: .
(Ⅰ)解:由已知得: . ……………1
分
由 为偶函数,得 为偶函数,
显然有
.
…………2分
又 ,所以 ,即 . …………3分
又因为 对一切实数 恒成立,
即对一切实数 ,不等式 恒成立. …………4分
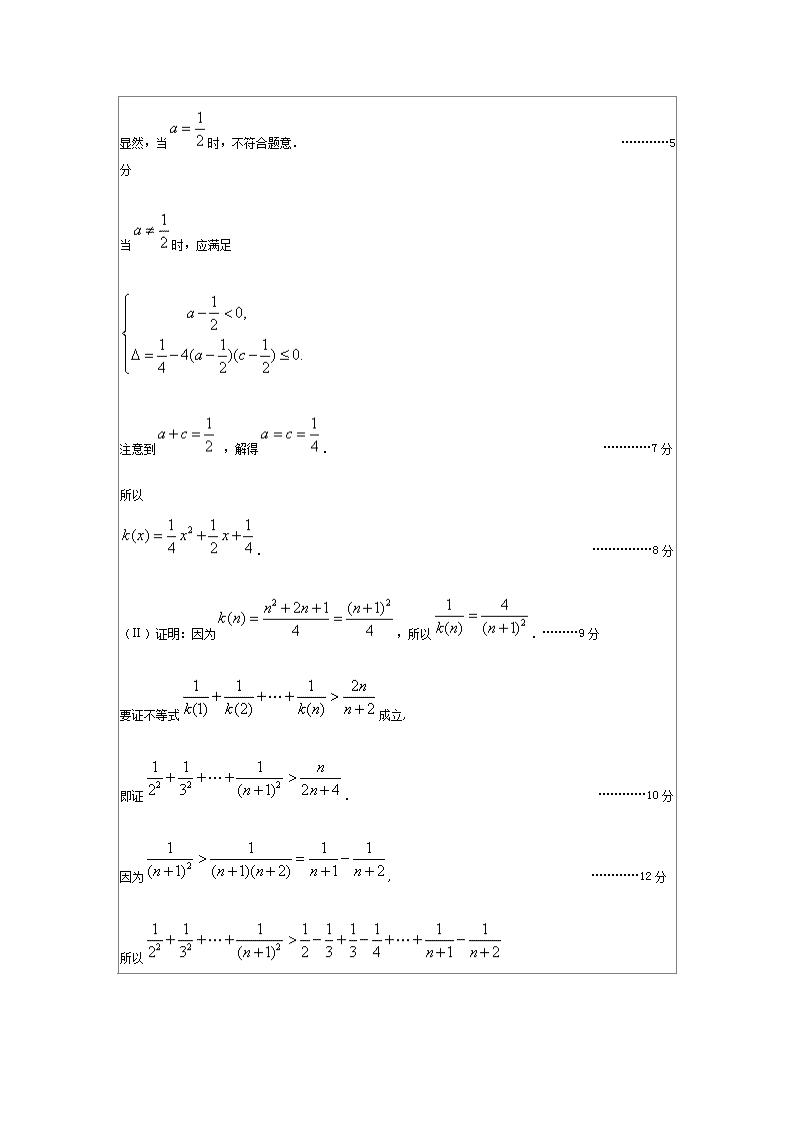
显然,当 时,不符合题意. …………5
分
当 时,应满足
注意到 ,解得 . …………7分
所以
. ……………8
分
(Ⅱ)证明:因为 ,所以 .………9分
要证不等式 成立,
即证 . …………10 分
因为 , …………12 分
所以
.
所以 成立. ……………14 分
2;已知函数:
(1)讨论函数 的单调性;
(2)若函数 的图像在点 处的切线的倾斜角为 ,问: 在什么范围取值时,函
数 在区间 上总存在极值?
(3)求证: .
解:(1) (1 分),
当 时, 的单调增区间为 ,减区间为 ;…………2分
当 时, 的单调增区间为 ,减区间为 ;…………3分
当 时, 不是单调函数…………4分
(2)因为函数 的图像在点 处的切线的倾斜角为 ,
所以 ,所以 , , ……………..…6分
,
…………………………………….……7分
要使函数 在区间 上总存在极值,所以只需
, ………………ks5u……..……9
分 解得 ………………………………………………………10
分
⑶令 此时 ,所以 ,
由⑴知 在 上单调递增,∴当 时 ,
即 ,∴ 对一切 成立,………12分
∵ ,则有 ,∴
…………14 分
来源: 江西省重点中学协作体 2012届高三联考(数学理)
已知函数 = , .
(Ⅰ)求函数 在区间 上的值域;
(Ⅱ)是否存在实数 ,对任意给定的 ,在区间 上都存在两个不同的 ,使
得 成立.若存在,求出 的取值范围;若不存在,请说明理由;
(Ⅲ)给出如下定义:对于函数 图象上任意不同的两点 ,如果对于函数
图象上的点 (其中 总能使得 成
立,则称函数具备性质“ ”,试判断函数 是不是具备性质“ ”,并说明理由.
解:(Ⅰ) 在区间 上单调递增,在区间
上单调递减,且
的值域为 ………………3分
(Ⅱ)令 ,则由(Ⅰ)可得 ,原问题等价于:对任意的 在
上总有两个不同的实根,故 在 不可能是单调函数 …………………5 分
当 时, ,.s 在区间 上递减,不合题意
当 时, , 在区间 上单调递增,不合题意
当 时, , 在区间 上单调递减,不合题意
当 即 时, 在区间 上单调递减; 在区间 上单递增,由上可
得 ,此时必有 的最小值小于等于 0 而由 可得
,则
综上,满足条件的 不存在。………………………..8 分
(Ⅲ)设函数 具备性质“ ”,即在点 处的切线斜率等于 ,不妨设 ,则
,而 在点 处的切线斜率
为 ,
故有 ………………10 分
即 ,令 ,则上式化为 ,
………………12 分
令 ,则由 可得 在 上单调递增,
故 ,即方程 无解,所以函数 不具备性质
“ ”. ……………………14分
3;已知 a>0,函数 .
(Ⅰ)设曲线 在点(1,f(1))处的切线为 ,若 与圆 相切,求 a的值;
(Ⅱ)求函数 f(x)的单调区间;
(Ⅲ)求函数 f(x)在[0,1]上的最小值.
解:(Ⅰ)依题意有
过点 的切线的斜率为 ,
则过点 的直线方程为 ……………………………………… 2分
又已知圆的圆心为(-1,0),半径为 1
∴ ,解得 ……………………………………………………… 4分
(Ⅱ)
∵ ,∴
令 解得 ,令 ,解得
所以 的增区间为 ,减区间是 ………………………………8分
(Ⅲ) 当 ,即 时, 在[0,1]上是减函数
所以 的最小值为 …………………………………………………………9分
‚当 即 时
在 上是增函数,在 是减函数…………………………………10 分
所以需要比较 和 两个值的大小
因为 ,所以
∴当 时最小值为 a,
当 时,最小值为 ………………………………………………………12 分
ƒ当 ,即 时, 在[0,1]上是增函数
所以 最小值为 …………………………………………………………………13分
综上,当 时, 为最小值为 a
当 时, 的最小值为 .……………………………………………………14 分
难度: 使用次数:25 入库时间:2011-12-01
[+]试题篮
来源: 浙江省绍兴市绍兴一中 2011学年第一学期高三期中考试试卷 数学(理)
已知函数
(Ⅰ)若函数 是定义域上的单调函数,求实数 的最小值;
(Ⅱ)方程 有两个不同的实数解,求实数 的取值范围;
(Ⅲ)在函数 的图象上是否存在不同两点 ,线段 的中点的横坐标为 ,
有 成立?若存在,请求出 的值;若不存在,请说明理由.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解(Ⅰ) 1分
若函数 在 上递增,则 对 恒成立,即 对 恒成立,
而当 时,
若函数 在 上递减,则 对 恒成立,即 对 恒成立,
这是不可能的.
综上, 的最小值为
1. 4
分
(Ⅱ)解 1、由
令
得 =0的根为 1,所以
当 时, ,则 单调递增,当 时, ,则 单调递减,
所以 在 处取到最大值 ,又 , ,
所以要使 与 有两个不同的交点,则有
……………8 分
(Ⅲ)假设存在,不妨设
9 分
若 则 ,即 ,即 . (*) 12 分
令 , ( ),
则 >0.∴ 在 上增函数, ∴ ,
∴(*)式不成立,与假设矛盾.∴
因此,满足条件的 不存
在. 15
分
难度: 使用次数:21 入库时间:2011-11-28
[+]试题篮
来源: 湖北省鄂州市 2012届高三摸底考试数学试题(理科)
已知函数:
⑴讨论函数 的单调性;
⑵若函数 的图象在点 处的切线的倾斜角为 45
o
,对于任意的 ,函数
在区间 上总不是单调函数,求 m的取值范围;
⑶求证: .
答案 >>
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
难度: 使用次数:23 入库时间:2011-11-11
[+]试题篮
来源: 江苏省苏北四市 2012届高三第一次调研测试(数学)
已知正方形 的中心在原点,四个顶点都在函数 图象上.
(1)若正方形的一个顶点为 ,求 , 的值,并求出此时函数的单调增区间;
(2)若正方形 唯一确定,试求出 的值.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
⑴因为 ,所以 ,因此 ,
所以函数 的图象在点 处的切线方程为 ,…………………………2分
由 得 ,由 ,得 .…4分
⑵因为 ,
所以 ,由题意知 在 上有解,
因为 ,设 ,因为 ,
则只要 解得 ,
所以 b的取值范围 .………………………………………………………………8 分
⑶不妨设 .因为函数 在区间 上是增函数,所以 ,
函数 图象的对称轴为 ,且 ,
(ⅰ)当 时,函数 在区间 上是减函数,所以 ,
所以 等价于 ,
即 ,
等价于 在区间 上是增函数,
等价于 在区间 上恒成立,
等价于 在区间 上恒成立,
所以 ,又 ,
所以 ;………………………………………………………………………………………10分
(ⅱ)当 时,函数 在区间 上是减函数,在 上为增函数.
①当 时,
等价于 ,
等价于 在区间 上是增函数,
等价于 在区间 上恒成立,
等价于 在区间 上恒成立,
所以 ,又 ,
所以 ;……………………………………………………………………………12 分
②当 时,
等价于 ,
等价于 在区间 上是增函数,
等价于 在区间 上恒成立,
等价于 在区间 上恒成立,
所以 ,故 .………………………………………………………………14分
③当 时,
由 图象的对称性知,只要 对于①②同时成立,那么对于③,
则存在 ,
使 恒成立;
或存在 ,
使 恒成立.
因此, .
综上,b的取值范围是 .……………………………………………………16 分
难度: 使用次数:21 入库时间:2011-10-23
[+]试题篮
来源: 扬州市中学 2011~2012学年度第一学期期初调研测试高三数学试题
已知函数 ( 是自然对数的底数).
(1)若曲线 在 处的切线也是抛物线 的切线,求 的值;
(2)若对于任意 恒成立,试确定实数 的取值范围;
(3)当 时,是否存在 ,使曲线 在点 处的切线斜率
与 在 上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解:(1) ,所以在 处的切线为
即:
………………………………2 分
与 联立,消去 得 ,
由 知, 或 . ………………………………4分
(2)
①当 时, 在 上单调递增,且当 时, ,
,故 不恒成立,所以 不合题意 ;………………6分
②当 时, 对 恒成立,所以 符合题意;
③当 时令 ,得 , 当 时, ,
当 时, ,故 在 上是单调递减,在 上
是单调递增, 所以 又 ,
,
综上: . ………………………………10 分
(3)当 时,由(2)知 ,
设 ,则 ,
假设存在实数 ,使曲线 在点 处的切线斜率与 在 上
的最小值相等, 即为方程的解,………………………………13 分
令 得: ,因为 , 所以 .
令 ,则 ,
当 是 ,当 时 ,所以 在 上单调递减,
在 上单调递增, ,故方程 有唯一解为 1,
所以存在符合条件的 ,且仅有一个 . ……………………16 分
难度: 使用次数:16 入库时间:2011-08-10
[+]试题篮
来源: 安徽省宣城市 2011届高三第二次调研测试数学(理)试题
已知函数 .
⑴若曲线 在 处的切线方程为 ,求实数 和 的值;
⑵求证; 对任意 恒成立的充要条件是 ;
⑶若 ,且对任意 、 ,都 ,求 的取值范围.
答案 >>
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
难度: 使用次数:20 入库时间:2011-06-20
[+]试题篮
来源: 2011年普通高等学校招生统一考试湖南省理科数学卷解析
已知函数 ( ) = ,g ( )= + 。
(Ⅰ)求函数 h ( )= ( )-g ( )的零点个数。并说明理由;
(Ⅱ)设数列{ }( )满足 , ,证明:存在常数 M,使得 对
于任意的 ,都有 ≤ .
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
难度: 使用次数:18 入库时间:2011-06-20
[+]试题篮
来源: 2011年普通高等学校招生统一考试湖南省理科数学卷解析
已知函数 ( ) = ,g ( )= + 。
(Ⅰ)求函数 h ( )= ( )-g ( )的零点个数。并说明理由;
(Ⅱ)设数列{ }( )满足 , ,证明:存在常数 M,使得 对
于任意的 ,都有 ≤ .
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
难度: 使用次数:30 入库时间:2011-06-16
[+]试题篮
来源: 2011年普通高等学校招生全国统一考试
已知函数 ,曲线 在点 处的切线方程为 .
(I)求 a,b的值;
(II)如果当 x>0,且 时, ,求 k的取值范围.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解:
(Ⅰ)
由于直线 的斜率为 ,且过点 ,故 即
解得 ,
。
(Ⅱ)由(Ⅰ)知 ,所以
。
考虑函数 ,则
。
(i)设 ,由 知,当 时, 。而 ,
故
当 时, ,可得 ;
当 x (1,+ )时,h(x)<0,可得 h(x)>0
从而当 x>0,且 x 1 时,f(x)-( + )>0,即 f(x)> + .
(ii)设 0
0,故 (x)>0,而
h(1)=0,故当 x (1, )时,h(x)>0,可得 h(x)<0,与题设矛盾。
(iii)设 k 1.此时 (x)>0,而 h(1)=0,故当 x (1,+ )时,h(x)>0,可得 h(x)
<0,与题设矛盾。
综合得,k 的取值范围为(- ,0]
解:(2)由(1)知 .
故要证: 只需证
为去分母,故分 x>1 与 01 时,需证
即 即需证 . (1)
设 ,则
由 x>1 得 ,所以 在(1,+ )上为减函数.又因 g(1)=0
所以 当 x>1 时 g(x)<0 即(1)式成立.
同理 00 时, ,因为 ,所以
在 上恒成立,故 F(x)在 上单调递
增, ,故 m 的取值范围是
…………(15分)
另法:(3) 令
难度: 使用次数:43 入库时间:2011-05-08
[+]试题篮
来源: 黑龙江省哈三中四校联考 2011届高三一模考试(数学理)
已知函数 ( , ), .
(Ⅰ)证明:当 时,对于任意不相等的两个正实数 、 ,均有
成立;
(Ⅱ)记 ,
(ⅰ)若 在 上单调递增,求实数 的取值范围;
(ⅱ)证明: .
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
(Ⅰ)证明: ,
,
,则 ①
,则 ,②
由①②知 .……………………………… 分
(Ⅱ)(ⅰ) ,
,
令 ,则 在 上单调递增.
,则当 时, 恒成立,
即当 时, 恒成立. …………………………… 5 分
令 ,则当 时, ,
故 在 上单调递减,从而 ,
故 .……………………………………………………7分
(ⅱ)法一:
,
令 ,
则 表示 上一点 与直线 上一点 距离的平方.… 8 分
令 ,则 ,
可得 在 上单调递减,在 上单调递增,
故 ,则 ,…………………………………… 10 分
直线 与 的图象相切与点 ,
点 到直线 的距离为 ,
则 ,
故 .……………………………………………………12分
法二:
,
令 ,则 .………………8分
令 ,则 ,显然 在 上单调递减,在 上单调
递增,………………………………………………………………………………10 分
则 ,则 ,故 .…………………12 分
难度: 使用次数:55 入库时间:2011-04-29
[+]试题篮
来源: 陕西省西安市 2011届高三五大名校第一次模拟考试(数学理)
已知函数 ,函数 是区间[-1,1]上的减函数.
(I)求 的最大值;
(II)若 上恒成立,求 t的取值范围;
(Ⅲ)讨论关于 x的方程 的根的个数.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解:(I) ,
上单调递减,
在[-1,1]上恒成立, ,故 的最大值为 ……4分
(II)由题意
(其中 ),恒成立,
令 ,
则 ,
恒成立,
…………9 分
(Ⅲ)由
令
当
上为增函数;
当 时,
为减函数;
当
而
方程无解;
当 时,方程有一个根;
当 时,方程有两个根. …………14 分
难度: 使用次数:53 入库时间:2011-04-22
[+]试题篮
来源: 湖南省长沙长望浏宁四县市 2011届高三 3月调研考试数学(理)试题
(本小题满分 13 分)
已知函数 , 为正常数.
(1)若 ,且 ,求函数 的单调增区间;
(2)若 ,且对任意 , ,都有 ,求 的的
取值范围.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解:⑴ ,…2分
∵ ,令 ,得 ,或 ,
∴函数 的单调增区间为 , 。 6分
⑵∵ ,∴ ,
∴ , 8分
设 ,依题意, 在 上是减函数。
当 时, , ,
令 ,得: 对 恒成立,
设 ,则 ,
∵ ,∴ ,
∴ 在 上是增函数,则当 时, 有最大值为 ,
∴ 。
10 分
当 时, , ,
令 ,得: ,
设 ,则 ,
∴ 在 上是增函数,∴ ,
∴ ,
12 分
综上所述, . 13
分
难度: 使用次数:54 入库时间:2011-04-19
[+]试题篮
来源: 山东省潍坊三县 2011届高三阶段性教学质量检测数学(理)试题
(本小题满分 14分)
已知
(1)求函数 上的最小值;
(2)对一切 恒成立,求实数 的取值范围;
(3)证明:对一切 ,都有 成立.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
解:(1)由已知知函数 的定义域为 , ,……………1分
当 单调递减,当 单调递增.…2 分
① ,没有最小值; ……………………………………………………3分
② ,即 时, ; …………………4分
③ ,即 时, 上单调递增, ; 5分
所以 ……………………………………………6分
(2) ,则 ,…………………………7分
设 ,则 ,
① 单调递减,
② 单调递增,
所以 ,对一切 恒成立,
所以 ;………………………………………………10分
(3)问题等价于证明 ,…………………………11 分
由(1)可知 的最小值是 ,当且仅当 时取到,
设 ,则 ,
易知 ,当且仅当 时取到,…………………………13分
从而对一切 ,都有 成立 ……………………14 分
难度: 使用次数:86 入库时间:2011-04-07
[+]试题篮
来源: 广东省深圳市 2011届高三第一次模拟考试数学(理)试题
(本小题满分 14分)
已知函数 .
(1)当 时,如果函数 仅有一个零点,求实数 的取值范围;
(2)当 时,试比较 与 的大小;
(3)求证: ( ).
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1)当 时, ,定义域是 ,
, 令 ,得 或 . …2分
当 或 时, ,当 时, ,
函数 在 、 上单调递增,在 上单调递减. ……………4分
的极大值是 ,极小值是 .
当 时, ; 当 时, ,
当 仅有一个零点时, 的取值范围是 或 .……………5 分
(2)当 时, ,定义域为 .
令 ,
,
在 上是增函
数. …………………………………7 分
①当 时, ,即 ;
②当 时, ,即 ;
③当 时, ,即 . …………………………………9分
(3)(法一)根据(2)的结论,当 时, ,即 .
令 ,则有 , . ……………12 分
. …………………………………
…14 分
(法二)当 时, .
, ,即 时命题成立. ………………………………10分
设当 时,命题成立,即 .
时, .
根据(2)的结论,当 时, ,即 .
令 ,则有 ,
则有 ,即 时命题也成立.……………13 分
因此,由数学归纳法可知不等式成
立. ………………………………14 分
(法三)如图,根据定积分的定义,
得 .……11 分
,
. ………………………………12分
,
又 , ,
.
. …………………………………
14 分
【说明】本题主要考查函数导数运算法则、利用导数求函数的极值、证明不等式等基础知识,考查分类讨
论思想和数形结合思想,考查考生的计算能力及分析问题、解决问题的能力和创新意识.
难度: 使用次数:42 入库时间:2011-04-07
[+]试题篮
来源: 广东省深圳市 2011届高三第一次模拟考试数学(理)试题
(本小题满分 14分)
已知函数 .
(1)当 时,如果函数 仅有一个零点,求实数 的取值范围;
(2)当 时,试比较 与 的大小;
(3)求证: ( ).
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1)当 时, ,定义域是 ,
, 令 ,得 或 . …2分
当 或 时, ,当 时, ,
函数 在 、 上单调递增,在 上单调递减. ……………4分
的极大值是 ,极小值是 .
当 时, ; 当 时, ,
当 仅有一个零点时, 的取值范围是 或 .……………5 分
(2)当 时, ,定义域为 .
令 ,
,
在 上是增函
数. …………………………………7 分
①当 时, ,即 ;
②当 时, ,即 ;
③当 时, ,即 . …………………………………9分
(3)(法一)根据(2)的结论,当 时, ,即 .
令 ,则有 , . ……………12 分
,[来源:学科网 ZXXK]
. …………………………………
…14 分
(法二)当 时, .
, ,即 时命题成立. ………………………………10分
设当 时,命题成立,即 .
时, .
根据(2)的结论,当 时, ,即 .
令 ,则有 ,
则有 ,即 时命题也成立.……………13 分
因此,由数学归纳法可知不等式成
立. ………………………………14 分
(法三)如图,根据定积分的定义,
得 .……11 分
,
. ………………………………12分
,
又 , ,
.
. …………………………………
14 分
【说明】本题主要考查函数导数运算法则、利用导数求函数的极值、证明不等式等基础知识,考查分类讨
论思想和数形结合思想,考查考生的计算能力及分析问题、解决问题的能力和创新意识.
难度: 使用次数:61 入库时间:2011-03-31
[+]试题篮
来源: 江西省重点中学联盟 2011届高三第一次联考(数学理)
(本题满分 14分)
已知函数 ( 为自然对数的底数).
(1)求 的最小值;
(2)不等式 的解集为 ,若 且 求实数 的取值范围;
(3)已知 ,且 ,是否存在等差数列 和首项为 公比大于 0的等比数
列 ,使得 ?若存在,请求出数列 的通项公
式.若不存在,请说明理由.
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1) 1分
由 当 ;当
…4分
(2) , 有解
由 即 上有解 …6 分
令 , 上减,在[1,2]
上增
又 ,且
… 8分
(3)设存在公差为 的等差数列 和公比 首项为 的等比数列 ,使
…10分
又 时,
故
②-①×2得, 解得 (舍)
故 …12 分
此时
存在满足条件的数列 满足题意 …14 分
难度: 使用次数:70 入库时间:2011-03-30
[+]试题篮
来源: 山东省济南市 2011届高三教学质量调研(一模)数学(理)试题
(本小题满分 14分)
已知函数
(1) 当 时,求函数 的最值;
(2) 求函数 的单调区间;
(3) 试说明是否存在实数 使 的图象与 无公共点.
答案 >>
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
难度: 使用次数:63 入库时间:2011-03-28
[+]试题篮
来源: 浙江省温州中学 2011届高三三月月考数学(文)试题
已知函数 ,过点 P(0,m)作曲线 的切线,斜率恒大于零,则
的取值范围为 .
答案 <<
纠错[永久链接]
题型:填空题 知识点:2.4导数及其应用
难度: 使用次数:42 入库时间:2011-03-27
[+]试题篮
来源: 浙江省六校 2011届高三 2月联考数学(文)试题
已知二次函数 的导函数为 , 与 轴恰有一个交点,则
的最小值为 ( )
(A) 2 (B) (C) 3 (D)
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
A
难度: 使用次数:64 入库时间:2011-03-21
[+]试题篮
来源: 江苏省宿豫中学 2011届高三第二次模拟考试(数学)
已知函数
(1)、若函数 在 处的切线方程为 ,求 的值;
(2)、若函数 在 为增函数,求 的取值范围;
(3)、讨论方程 解的个数,并说明理由。
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1)因为: ,又 在 处的切线方程为
所以 解得: ………3分
(2)若函数 在 上恒成立。则 在 上恒成立,
即: 在 上恒成立。所以有 ……3 分
(3)当 时, 在定义域 上恒大于 ,此时方程无解;……7 分
当 时, 在 上恒成立,所以 在定义域 上为增函数。
, ,所以方程有惟一解。……8 分
当 时,
因为当 时, , 在 内为减函数;
当 时, 在 内为增函数。
所以当 时,有极小值即为最小值 。……10分
当 时, ,此方程无解;
当 时, 此方程有惟一解 。
当 时,
因为 且 ,所以方程 在区间 上有惟一解,……12 分
因为当 时, ,所以
所以
因为 ,所以
所以 方程 在区间 上有惟一解。
所以方程 在区间 上有惟两解。 ……14 分
综上所述:当 时,方程无解;
当 时,方程有惟一解;
当 时方程有两解。 ……14分
难度: 使用次数:94 入库时间:2009-03-17
[+]试题篮
来源: 2007年普通高等学校招生全国统一考试数学试卷(山东卷.理)
设函数 f(x)=x2
+b ln(x+1),其中 b≠0.
(Ⅰ)当 b> 时,判断函数 f(x)在定义域上的单调性;
(Ⅱ)求函数 f(x)的极值点;
(Ⅲ)证明对任意的正整数 n,不等式 ln )都成立.
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
(I) 函数 的定义域为 .
,
令 ,则 在 上递增,在 上递减,
.
当 时, ,
在 上恒成立.
即当 时,函数 在定义域 上单调递增。
(II)分以下几种情形讨论:
(1)由(I)知当 时函数 无极值点.
(2)当 时, ,
时,
时,
时,函数 在 上无极值点。
(3)当 时,解 得两个不同解 , .
当 时, , ,
此时 在 上有唯一的极小值点 .
当 时,
在 都大于 0 , 在 上小于 0 ,
此时 有一个极大值点 和一个极小值点 .
综上可知, 时, 在 上有唯一的极小值点 ;
时, 有一个极大值点 和一个极小值点 ;
时,函数 在 上无极值点。
(III) 当 时,
令 则
在 上恒正,
在 上单调递增,当 时,恒有 .
即当 时,有 ,
对任意正整数 ,取 得
难度: 使用次数:70 入库时间:2009-03-17
[+]试题篮
来源: 2008年普通高等学校招生全国统一考试(山东卷.理)
已知函数 ,其中 ,a为常数
(Ⅰ)当 时,求函数 的极值;
(Ⅱ)当 时,证明:对任意的正整数 n,当 时,有
答案 <<
纠错[永久链接]
题型:计算题 知识点:2.4导数及其应用
(Ⅰ)解:由已知得函数 的定义域为 ,
当 n=2 时,
所以 .
(1)当 a>0时,由 =0 得 >1, <1,
(2)此时 = .
当 x∈(1,x1)时, <0, 单调递减;
当 x∈(x1+∞)时, >0, 单调递增.
当 a≤0时, <0 恒成立,所以 无极值.
综上所述,n=2 时,
当 a>0时, 在 处取得极小值,极小值为
当 a≤0时, 无极值.
(Ⅱ)证法一:因为 a=1,所以
当 n为偶数时,
令
则 =1+ >0(x≥2).
所以当 x∈[2,+∞]时,g(x)单调递增,
又 g(2)=0
因此 ≥g(2)=0 恒成立,
所以 f(x)≤x-1 成立.
当 n为奇数时,
要证 ≤x-1,由于 <0,所以只需证 ,
令 ,
则 =1- ≥0(x≥2),
所以当 x∈[2,+∞]时, 单调递增,又 h(2)=1>0,
所以当 x≥2时,恒有 >0,即 命题成立.
综上所述,结论成立.
证法二:当 a=1 时,
当 x≤2,时,对任意的正整数 n,恒有 ≤1,
故只需证明 .
令
则
当 x≥2时, ≥0,故 h(x)在 上单调递增,
因此 当 x≥2时,h(x)≥h(2)=0,即 1+ln(x-1) ≤x-1 成立.
故 当 x≥2时,有 ≤x-1.
即 f(x)≤x-1.
难度: 使用次数:103 入库时间:2009-03-17
[+]试题篮
来源: 2008年广东省珠海市高三年级第一次统一考试(文)
设函数 ,其中 为常数.
(1)当 时,判断函数 在定义域上的单调性;
(2)若函数 的有极值点,求 的取值范围及 的极值点;
(3)求证对任意不小于 3的正整数 ,不等式 都成立.
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1)由题意知, 的定义域为 ,
当 时, ,函数 在定义域 上单调递增.
(2)①由(Ⅰ)得,当 时,函数 无极值点.
② 时, 有两个相同的解 ,
时,
时,函数 在 上无极值点.
③当 时, 有两个不同解,
时, ,
,
此时 , 随 在定义域上的变化情况如下表:
减 极小值 增
由此表可知: 时, 有惟一极小值点 ,
ii) 当 时,0< <1
此时, , 随 的变化情况如下表:
增 极大值 减 极小值 增
由此表可知: 时, 有一个极大值 和一个极小值点
;
综上所述:
当且仅当 时 有极值点;
当 时, 有惟一最小值点 ;
当 时, 有一个极大值点 和一个极小值点
(3)由(2)可知当 时,函数 ,
此时 有惟一极小值点
且
难度: 使用次数:115 入库时间:2009-03-17
[+]试题篮
来源: 2008年 5月山东省实验中学高三模拟考试(理)
设函数 ,其中 为常数.
(Ⅰ)当 时,判断函数 在定义域上的单调性;
(Ⅱ)若函数 的有极值点,求 的取值范围及 的极值点;
(Ⅲ)当 且 时,求证: .
答案 <<
纠错[永久链接]
题型:综合题 知识点:2.4导数及其应用
解:(1)由题意知, 的定义域为 ,
当 时, ,函数 在定义域 上单调递增.
(2)①由(Ⅰ)得,当 时,函数 无极值点.
② 时, 有两个相同的解 ,
时,
时,函数 在 上无极值点.
③当 时, 有两个不同解,
时, ,
,
此时 , 随 在定义域上的变化情况如下表:
减 极小值 增
由此表可知: 时, 有惟一极小值点 ,
ii) 当 时,0< <1
此时, , 随 的变化情况如下表:
增 极大值 减 极小值 增
由此表可知: 时, 有一个极大值 和一个极小值点
;
综上所述:
当且仅当 时 有极值点;
当 时, 有惟一最小值点 ;
当 时, 有一个极大值点 和一个极小值点
(3)由(2)可知当 时,函数 ,
此时 有惟一极小值点
且
令函数