- 2021-06-10 发布 |
- 37.5 KB |
- 7页

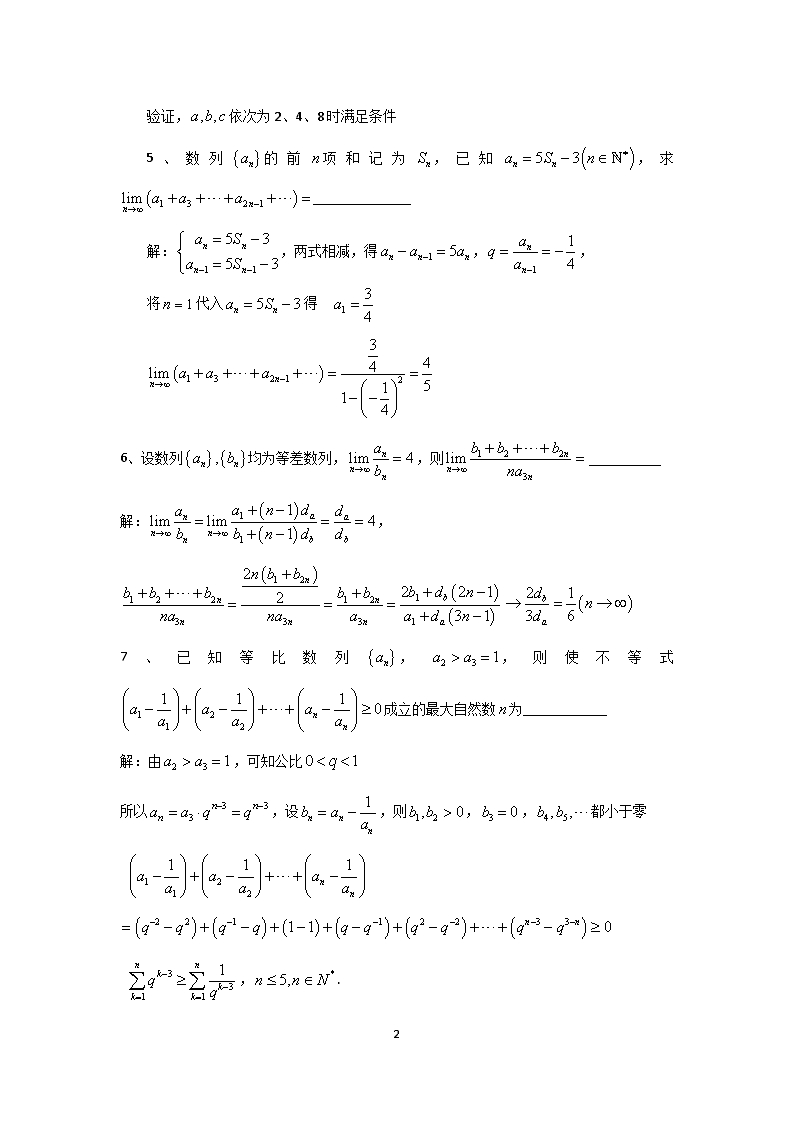

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市彭浦中学2014-2015学年高二第一学期第一次月考数学试题
彭浦中学2014学年第一学期第一次月考(高二) 一、填空题(每小题3分,共30分) 1、如果,那么_________ 解:由得, ,解得 2、已知各项均为正数的等比数列的首项,公比为,前项和为,若,则公比为的取值范围是_____________ 解:首先数列为各项均为正数等比数列,公比, 其次若时,,易验证满足条件; 若时,, ∴ 3、若数列中,,且对任意的正整数都有,则若时,_________ 解:,若时,是首项和公比都为的等比数列, 是首项和公比都为的等比数列, 4、设是满足的整数,若成等比数列,则的值依次为__________ 2、4、8 解: 由成等比数列,得, 7 验证,依次为2、4、8时满足条件 5、数列的前项和记为,已知,求______________ 解:,两式相减,得,, 将代入得 6、设数列均为等差数列,,则 解:, 7、已知等比数列,,则使不等式成立的最大自然数为____________ 解:由,可知公比 所以,设,则,,都小于零 ,. 7 故答案为5 8、设数列的前项和为,关于数列有下列三个命题: ①若即是等差数列,又是等比数列,则 ②若,则是等差数列; ③若,则是等比数列 这些命题中,真命题的序号是_____________ ①②③ 9、已知是定义域为正整数集的函数,具有如下性质:对于定义域内任意的,如果成立,则成立,那么下列命题正确的是_①③__ ①若成立,则对于任意,均有 ②若成立,则对于任意,均有 ③若成立,则对于任意,均有 解:②错误 其逆否命题为 ,与条件矛盾,故错误 ③正确 由条件知 其逆否命题为 故可以推出推出,依次可推出任意,均有 10、把数列的所有数按照从大到小的原则写成如下数表: 1 第行有个数,第行的第个数(从左数起)记为,则 7 解:是数列的第项,即第项, 是数列的第项,即第项,故 二、选择题(每小题3分,共12分) 11、下列命题中正确的是 ( D ) A.公差为0的等差数列是等比数列 B.成等比数列的充要条件是 C.公比的等比数列是递减数列 D.是成等差数列的充分不必要条件 解:A、B中都忽略了等比数列的公比不能为0,C中若首项为负,则数列为递增数列,故选 12、设是定义在上恒不为零的函数,且对任意的实数,都有,若,,则数列的前项和的取值范围是( D ) A. B. C. D. 解:,,,, ,而,∴ 13、若把正整数按图所示的规律排序,则从2002到2004年的箭头方向依次为( D ) A. B. C. D. 解:易得规律,所以,故选D 14、计算机是将信息转换成二进制数进行处理的,二进制即“逢二进一”,如: 7 表示二进制的数,将它转换成二进制的形式是 , 那么将二进制数转换成十进制的形式是( C ) A. B. C. D. 解,故选C 三、解答题(6分+6分+8分+12分+12分) 15、已知为等比数列的前项和,,,前项中的数值最大的项为54,求 解:, 而,所以数列是递增的数列,前项中的数值最大的项为,故, 16、已知数列满足 (1)求数列的通项公式;(2)求数列的前项和 解:(1)当时 两式相减,得 (2)设 则 7 两式相减,得 17、若为大于1的自然数,求证: 证明:当时,,不等式成立 假定时,不等式成立,即 当时, ,其中 由数学归纳法得命题成立 18、已知等差数列的公差不为0,其前项和为,等比数列的前项和为,公比为,且,求的值 解: 若时当时无极限, 若时 故当时,其他情形极限无意义 19、已知正项数列,,且 7 (1)求证:是等差数列,并求的通项公式; (2)数列满足,若,仍是中的项,求在区间中的所有可能值之和; (3)若将上述递推关系改为:,且数列中任意项,试求满足要求的实数的取值范围 解:(1)对两边取倒数,得,故是等差数列, 又,故 (2) 设是中的第项,则, 所以 (3)对两边取倒数,得, ,而,所以 7查看更多