【数学】2020届一轮复习(文)通用版7-3二元一次不等式(组)与简单的线性规划问题作业
课时跟踪检测(四十三) 二元一次不等式(组)与简单的线性规划问题
1.(2018·陕西部分学校摸底检测)若实数x,y满足则2x+y的最小值为
( )
A.- B.0
C.1 D.
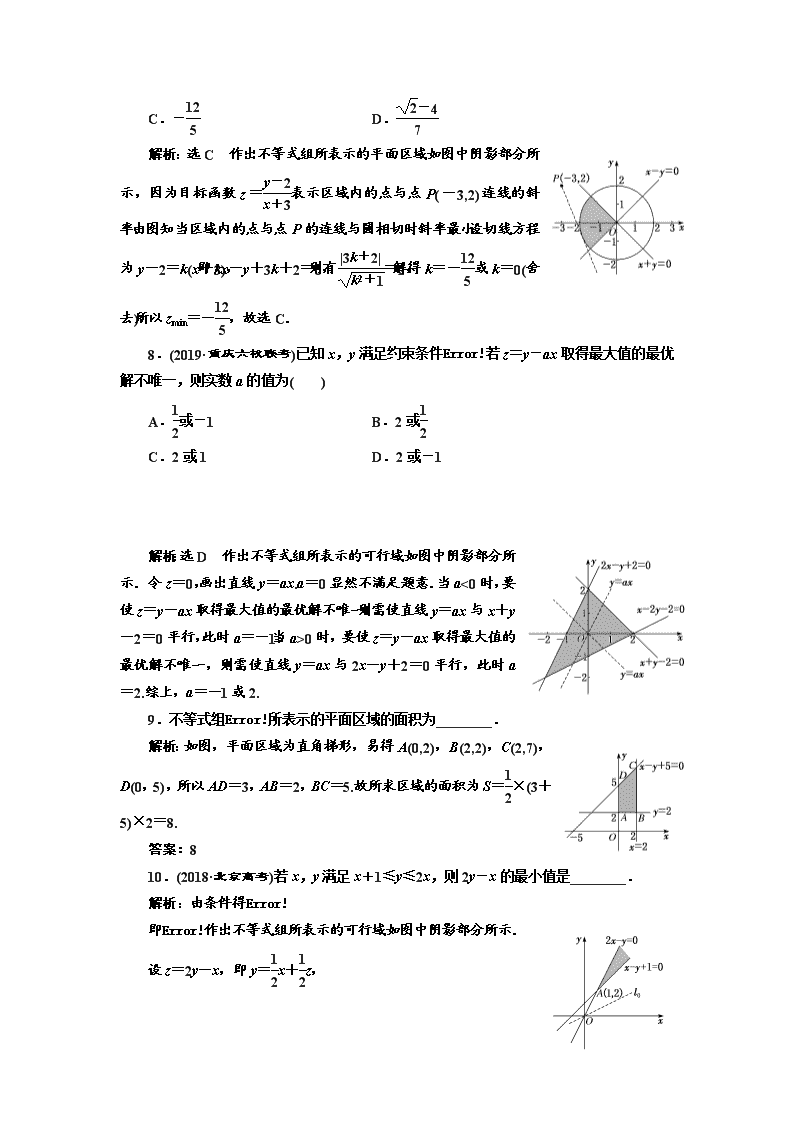
解析:选A 作出不等式组所表示的平面区域如图中阴影部分所示,令z=2x+y,作出直线y=-2x,平移该直线,当直线经过点A时,z=2x+y取得最小值,最小值为-,故选A.
2.不等式(x-2y+1)(x+y-3)≤0在坐标平面内表示的区域(用阴影部分表示)应是
( )
解析:选C (x-2y+1)(x+y-3)≤0⇔或结合图形可知选C.
3.(2019·郑州模拟)已知直线y=k(x+1)与不等式组表示的平面区域有公共点,则k的取值范围为( )
A.[0,+∞) B.
C. D.
解析:选C 作出不等式组表示的可行域如图中阴影部分所示(不包括直线y=0),直线y=k(x+1)过定点(-1,0),由解得过点(-1,0)与(1,3)的直线的斜率是,根据题意可知0
0时,要使z=y-ax取得最大值的最优解不唯一,则需使直线y=ax与2x-y+2=0平行,此时a=2.综上,a=-1或2.
9.不等式组所表示的平面区域的面积为________.
解析:如图,平面区域为直角梯形,易得A(0,2),B(2,2),C(2,7),D(0,5),所以AD=3,AB=2,BC=5.故所求区域的面积为S=×(3+5)×2=8.
答案:8
10.(2018·北京高考)若x,y满足x+1≤y≤2x,则2y-x的最小值是________.
解析:由条件得
即作出不等式组所表示的可行域如图中阴影部分所示.
设z=2y-x,即y=x+z,
作直线l0:y=x并向上平移,显然当l0过点A(1,2)时,z取得最小值,zmin=2×2-1=3.
答案:3
11.(2018·南阳模拟)已知O是坐标原点,点A(-1,1),若点M(x,y)为平面区域上的一个动点,则·的取值范围是________.
解析:作出不等式组表示的平面区域如图中阴影部分所示,因为点A(-1,1),点M(x,y),所以·=y-x,令y-x=m,平移直线y-x=m,由图可知,当直线经过点D(1,1)时,m取得最小值,且最小值为0,当直线经过点C(0,2)时,m取得最大值,且最大值为2,所以y-x的取值范围是[0,2],故·的取值范围是[0,2].
答案:[0,2]
12.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900 元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元.
解析:设生产A产品x件,B产品y件,
由已知可得约束条件为即
目标函数为z=2 100x+900y,
由约束条件作出不等式组表示的可行域如图中阴影部分所示.
作直线2 100x+900y=0,即7x+3y=0,当直线经过点M时,z取得最大值,
联立解得M(60,100).
则zmax=2 100×60+900×100=216 000(元).
答案:216 000
13.变量x,y满足
(1)设z1=4x-3y,求z1的最大值;
(2)设z2=,求z2的最小值;
(3)设z3=x2+y2,求z3的取值范围.
解:作出可行域如图中阴影部分所示,易得A,B(1,1),
联立解得C(5,2),
(1)z1=4x-3y⇔y=x-,易知平移直线y=x至过点C时,z1最大,且最大值为4×5-3×2=14.
(2)z2=表示可行域内的点与原点连线的斜率大小,显然直线OC斜率最小,故z2的最小值为.
(3)z3=x2+y2表示可行域内的点到原点距离的平方,而2=OB2
查看更多