新课程高中数学训练题组(必修3)全

新课程高中数学训练题组(必修3)全

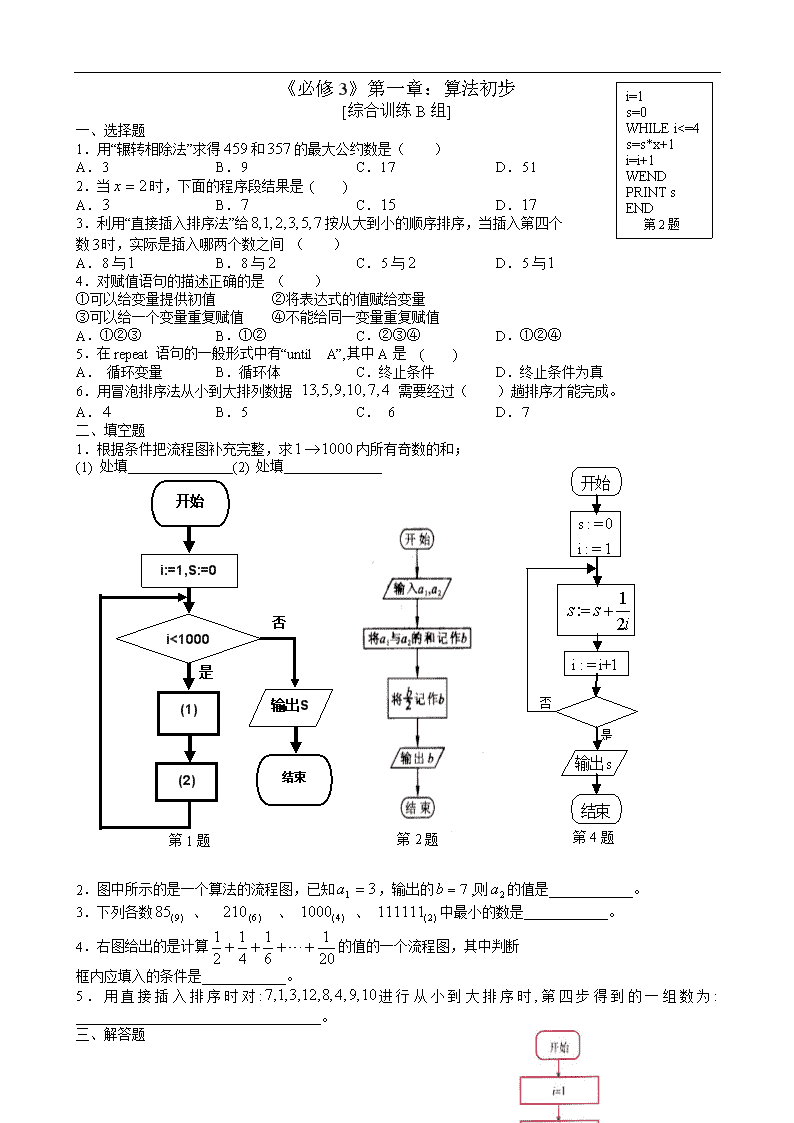
‎《必修3》第一章：算法初步 ‎[基础训练A组]‎ PRINT ，‎ 第4题 一、选择题 ‎1．下面对算法描述正确的一项是：（ ）‎ A．算法只能用自然语言来描述 B．算法只能用图形方式来表示 C．同一问题可以有不同的算法 D．同一问题的算法不同，结果必然不同 ‎2．用二分法求方程的近似根的算法中要用哪种算法结构（ ）‎ A．顺序结构 B．条件结构 C．循环结构 D．以上都用 ‎3．将两个数交换,使,下面语句正确一组是 ( )‎ IF THEN else PRINT y 第5题 a=b b=a c=b b=a a=c b=a a=b a=c c=b b=a A. B. C. D. ‎ ‎4．计算机执行下面的程序段后，输出的结果是（ ）‎ A． B． C． D．‎ ‎5．当时，下面的程序段输出的结果是（ ）‎ ‎ “n=”，n i =1‎ s=1‎ ‎ i< =‎ s=s*i i=i+1‎ ‎ ‎ PRINT s END 第1题 A． B． C． D．‎ 二、填空题 ‎1．把求的程序补充完整（右框图）‎ ‎2．用“冒泡法”给数列按从大到小进行排序时，经过第一趟排序后得到的新数列为 。‎ ‎3．用“秦九韶算法”计算多项式，当x=2时的值的过程中，要经过 次乘法运算和 次加法运算。‎ ‎4．以下属于基本算法语句的是 。‎ ‎①INPUT语句；②PRINT语句；③IF-THEN语句；④DO语句；⑤END语句；‎ ‎⑥WHILE语句；⑦END IF语句。‎ ‎5．将化成四进位制数的末位是____________。 ‎ 三、解答题 ‎1．把“五进制”数转化为“十进制”数，再把它转化为“八进制”数。‎ ‎2．用秦九韶算法求多项式当时的值。‎ ‎3．编写一个程序，输入正方形的边长，输出它的对角线长和面积的值。‎ ‎4．某市公用电话（市话）的收费标准为：分钟之内（包括分钟）收取元；超过分钟部分按元/分钟加收费。设计一个程序，根据通话时间计算话费。‎ i=1‎ s=0‎ WHILE i<=4‎ s=s*x+1‎ i=i+1‎ WEND PRINT s END 第2题 ‎《必修3》第一章：算法初步 ‎[综合训练B组]‎ 一、选择题 ‎1．用“辗转相除法”求得和的最大公约数是（ ）‎ A． B． C． D．‎ ‎2．当时，下面的程序段结果是 ( )‎ A． B． C． D．‎ ‎3．利用“直接插入排序法”给按从大到小的顺序排序，当插入第四个 数时，实际是插入哪两个数之间 （ ）‎ A．与 B．与 C．与 D．与 ‎4．对赋值语句的描述正确的是 （ ）‎ ‎①可以给变量提供初值 ②将表达式的值赋给变量 ‎③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A．①②③ B．①② C．②③④ D．①②④‎ ‎5．在repeat 语句的一般形式中有“until A”,其中A是 ( )‎ A． 循环变量 B．循环体 C．终止条件 D．终止条件为真 ‎6．用冒泡排序法从小到大排列数据 需要经过（ ）趟排序才能完成。‎ A． B． C． D．‎ 二、填空题 ‎1．根据条件把流程图补充完整，求内所有奇数的和； 第4题 (1) 处填 (2) 处填 ‎ 开始 i:=1,S:=0‎ i<1000‎ ‎(1)‎ ‎(2)‎ 输出S 结束 否 是 第1题 第2题 ‎2．图中所示的是一个算法的流程图，已知，输出的,则的值是____________。‎ ‎3．下列各数 、 、 、 中最小的数是____________。 ‎ ‎4．右图给出的是计算的值的一个流程图，其中判断 框内应填入的条件是____________。‎ ‎5．用直接插入排序时对:进行从小到大排序时,第四步得到的一组数为: ___________________________________。‎ 第1题 三、解答题 ‎1．以下是计算程序框图,请写出对应的程序。‎ ‎2．函数，写出求函数的函数值的程序。‎ ‎3．用辗转相除法或者更相减损术求三个数的最大公约数.‎ ‎ ‎ ‎4．意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序.‎ ‎《必修3》第一章：算法初步 n=5‎ s=0‎ WHILE s<15‎ ‎ S=s + n ‎ n=n－1‎ WEND PRINT n END ‎(第3题)‎ ‎[提高训练C组]‎ 一、选择题 ‎1.下列给出的赋值语句中正确的是（ ）‎ A． B． C． D．‎ ‎2.给出以下四个问题,①, 输出它的相反数. ②求面积为的正方形的周长.‎ ‎③求三个数中输入一个数的最大数. ④求函数的函数值. ‎ 其中不需要用条件语句来描述其算法的有 ( ) ‎ A. 个 B. 个 C. 个 D. 个 ‎3．右边程序执行后输出的结果是（ ）‎ a=0 ‎ j=1‎ WHILE j<=5‎ ‎ a=(a + j) MOD 5‎ ‎ j=j+1‎ WEND PRINT a END 第5题 A. B． C． D．‎ ‎4.用冒泡法对从小到大排序，需要（ ）趟排序。‎ A. B. C . D. ‎ ‎5. 右边程序运行后输出的结果为( )‎ A. B. C. D. ‎ ‎6．用冒泡法对一组数: 进行排序时,经过多少趟排序后,‎ 得到这一组数: ( )‎ A. B. C. D. ‎ 二、填空题 ‎1．三个数的最大公约数是_________________。 ‎ ‎2. 二进制数转换成十进制数是_________________.‎ INPUT “a，b，c =”;a，b，c IF b>a THEN t=a a=b b=t END IF IF c>a THEN t=a a=c c=t END IF IF c>b THEN t=b b=c c=t END IF ‎ PRINT a，b，c END 第4题 ‎3. 下左程序运行后输出的结果为_______________.‎ ‎ ‎ IF THEN ‎ ‎ ELSE ‎ ‎ END IF PRINT x－y ； y－x END ‎ 第3题 ‎4．右程序运行后实现的功能为_______________.‎ 三、解答题 ‎1．已知一个三角形的三边边长分别为，设计一个算法，‎ 求出它的面积。‎ ‎2．用二分法求方程在上的近似解，精确到，写出算法。画出流程图，并写出算法语句.‎ ‎《必修3》第二章：统计 ‎[基础训练A组]‎ 一、选择题 ‎1．名工人某天生产同一零件，生产的件数是设其平均数为,中位数为,众数为，则有( )‎ A． B． C． D．‎ ‎2．下列说法错误的是 ( )‎ A．在统计里，把所需考察对象的全体叫作总体 ‎ B．一组数据的平均数一定大于这组数据中的每个数据 ‎ C．平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 ‎ D．一组数据的方差越大，说明这组数据的波动越大 ‎3．某同学使用计算器求个数据的平均数时，错将其中一个数据输入为，那么由此求出的平均数与实际平均数的差是( )‎ A． B． C． D． ‎ ‎4. 要了解全市高一学生身高在某一范围的学生所占比例的大小，需知道相应样本的( )‎ A. 平均数 B. 方差 C. 众数 D. 频率分布 ‎ ‎5．要从已编号（）的枚最新研制的某型导弹中随机抽取枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的枚导弹的编号可能是（　　）‎ A． B． C． D．‎ ‎6．容量为的样本数据，按从小到大的顺序分为组，如下表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 频数 ‎10‎ ‎13‎ x ‎14‎ ‎15‎ ‎13‎ ‎12‎ ‎9‎ 第三组的频数和频率分别是 ( )‎ A．和 B．和 C． 和 D． 和 二、填空题 ‎1．为了了解参加运动会的名运动员的年龄情况，从中抽取名运动员；就这个问题，下列说法中正确的有　　　　；①名运动员是总体；②每个运动员是个体；③所抽取的名运动员是一个样本；④样本容量为；⑤这个抽样方法可采用按年龄进行分层抽样；⑥每个运动员被抽到的概率相等。‎ ‎2．经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的位“喜欢”摄影的同学、位“不喜欢”摄影的同学和位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人。‎ ‎3．数据的标准差是______________‎ ‎4．数据的方差为，平均数为，则（1）数据的标准差为　　　　，平均数为　　　　 ．（2）数据的标准差为　　　　，平均数为　　　　‎ ‎5．观察新生婴儿的体重，其频率分布直方图如图所示，则新生婴儿体重在的频率为　　　‎ ‎2400 2700 3000 3300 3600 3900 体重 ‎0‎ ‎0.001‎ 频率/组距 三、解答题 ‎1．对某校初二男生抽取体育项目俯卧撑，被抽到的名学生的成绩如下：‎ 成绩（次）‎ ‎10‎ ‎9‎ ‎8‎ ‎7‎ ‎6‎ ‎5‎ ‎4‎ ‎3‎ 人数 ‎8‎ ‎6‎ ‎5‎ ‎16‎ ‎4‎ ‎7‎ ‎3‎ ‎1‎ 试求全校初二男生俯卧撑的平均成绩。‎ ‎2．为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：‎ 组　别 频数 频率 ‎145.5～149.5‎ ‎1‎ ‎0.02‎ ‎149.5～153.5‎ ‎4‎ ‎0.08‎ ‎153.5～157.5‎ ‎20‎ ‎0.40‎ ‎157.5～161.5‎ ‎15‎ ‎0.30‎ ‎161.5～165.5‎ ‎8‎ ‎0.16‎ ‎165.5～169.5‎ M n 合　计 M N ‎（1）求出表中所表示的数分别是多少？‎ ‎（2）画出频率分布直方图.‎ ‎（3）全体女生中身高在哪组范围内的人数最多？‎ ‎3． 某校高中部有三个年级，其中高三有学生人，现采用分层抽样法抽取一个容量为的样本，已知在高一年级抽取了人，高二年级抽取了人，则高中部共有多少学生？ ‎ ‎4．从两个班中各随机的抽取名学生，他们的数学成绩如下： ‎ 甲班 ‎76‎ ‎74‎ ‎82‎ ‎96‎ ‎66‎ ‎76‎ ‎78‎ ‎72‎ ‎52‎ ‎68‎ 乙班 ‎86‎ ‎84‎ ‎62‎ ‎76‎ ‎78‎ ‎92‎ ‎82‎ ‎74‎ ‎88‎ ‎85‎ 画出茎叶图并分析两个班学生的数学学习情况。‎ ‎《必修3》第二章：统计 ‎[综合训练B组]‎ 一、选择题 ‎1．数据的方差为，则数据的方差为（　　）‎ A． B． C． D．‎ ‎2．某初级中学有学生人,其中一年级人,二、三年级各人,现要利用抽样方法取人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为;使用系统抽样时,将学生统一随机编号,并将整个编号依次分为段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250; ②5,9,100,107,111,121,‎ ‎180,195,200,265; ③11,38,65,92,119,146,173,200,227,254; ④30,57,84,111,138,165,192,219,246,270; ‎ 关于上述样本的下列结论中，正确的是（ ） ‎ A．②、③都不能为系统抽样 B．②、④都不能为分层抽样 C．①、④都可能为系统抽样 D．①、③都可能为分层抽样 ‎3．一个容量为的样本数据分组后组数与频数如下：［25，25.3），6；［25.3，25.6），4；［25.6，25.9），10；［25.9，26.2），8；［26.2，26.5），8；［26.5，26.8），4；则样本在［25，25.9）上的频率为（　　）‎ A． B． C． D．‎ ‎4．设有一个直线回归方程为，则变量增加一个单位时（　　）‎ A.平均增加1.5个单位 B.平均增加2个单位 C.平均减少1.5个单位 D.平均减少2个单位 ‎5．在一次歌手大奖赛上，七位评委为歌手打出的分数如下：, , , , , , ,‎ 去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )‎ A． B． C． D．‎ 二、填空题 ‎1．已知样本的平均数是，标准差是，则 ‎ ‎2．一个容量为的样本，已知某组的频率为，则该组的频数为__________‎ ‎3．用随机数表法从名学生（男生人）中抽取人进行评教，某男生被抽取的机率是_________‎ ‎4． 一个容量为的样本数据，分组后组距与频数如下表：‎ 组距 频数 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎4‎ ‎2‎ 则样本在区间 上的频率为__________________。‎ ‎5．某单位有老年人人，中年人人，青年人人，为调查身体健康状况，需要从中抽取一个容量为的样本，用分层抽样方法应分别从老年人、中年人、青年人中各抽取 ___人、 人、 人。‎ 三、解答题 ‎1．对甲、乙的学习成绩进行抽样分析，各抽门功课，得到的观测值如下：‎ 问：甲、乙谁的平均成绩最好？谁的各门功课发展较平衡？‎ 时速（km）‎ ‎0.01‎ ‎0.02‎ ‎0.03‎ ‎0.04‎ 频率 组距 ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎2．某学校共有教师人，其中不到岁的有人，岁及以上的有人。为了了解普通话在该校中的推广普及情况，用分层抽样的方法，从全体教师中抽取一个容量为人的样本进行普通话水平测试，其中在不到岁的教师中应抽取的人数为多少人？‎ ‎3．已知辆汽车通过某一段公路时的时速的频率分布直方图 如右图所示，求时速在的汽车大约有多少辆？‎ ‎《必修3》第二章：统计 ‎[提高训练C组]‎ 一、选择题 ‎1．某企业有职工人，其中高级职称人，中级职称人，一般职员人，现抽取人进行分层抽样，则各职称人数分别为（ ）‎ A． B． C． D．‎ ‎2. 从个编号中抽取个号码入样，若采用系统抽样方法进行抽取，则分段间隔应为（ ）‎ A． B． C． D.‎ ‎3. 有件产品编号从到,现在从中抽取件检验,用系统抽样确定所抽取的编号为( )‎ A． B． C． D．‎ ‎4．用样本频率分布估计总体频率分布的过程中，下列说法正确的是（ ）‎ A．总体容量越大，估计越精确 B．总体容量越小，估计越精确 C．样本容量越大，估计越精确 D．样本容量越小，估计越精确 ‎5．对于两个变量之间的相关系数，下列说法中正确的是（ ）‎ A．越大，相关程度越大 B．，越大，相关程度越小，越小，相关程度越大 C．且越接近于，相关程度越大；越接近于，相关程度越小 D．以上说法都不对 二、填空题 ‎1．相关关系与函数关系的区别是 ． ‎ ‎2．为了了解名学生对学校某项教改试验的意见，打算从中抽取一个容量为的样考虑用系统抽样，则分段的间隔为_______________ ‎ ‎3．从个篮球中任取一个，检验其质量，则应采用的抽样方法为_______________。 ‎ ‎4．采用简单随机抽样从含个个体的总体中抽取一个容量为的样本，个体 前两次未被抽到，第三次被抽到的概率为_____________________‎ ‎5．甲，乙两人在相同条件下练习射击，每人打发子弹，命中环数如下 ‎ 甲 ‎ 6‎ ‎ 8‎ ‎ 9‎ ‎ 9‎ ‎ 8‎ 乙 ‎ 10‎ ‎ 7‎ ‎ 7‎ ‎ 7‎ ‎ 9‎ 则两人射击成绩的稳定程度是__________________。‎ 三、解答题 ‎1．如图，从参加环保知识竞赛的学生中抽出名，‎ 将其成绩（均为整数）整理后画出的频率分布直方 图如右：观察图形，回答下列问题： ‎ ‎（1）这一组的频数、频率分别是多少？‎ ‎（2）估计这次环保知识竞赛的及格率（分及以 上为及格）‎ ‎2．以下是某地搜集到的新房屋的销售价格和房屋的面积的数据： ‎ ‎（1）画出数据对应的散点图；‎ ‎（2）求线性回归方程，并在散点图中加上回归直线；‎ ‎（3）据（2）的结果估计当房屋面积为时的销售价格.‎ ‎ ‎ ‎《必修3》第三章：概率 ‎[基础训练A组]‎ 一、选择题 ‎1．下列叙述错误的是（ ）‎ A． 频率是随机的,在试验前不能确定,随着试验次数的增加,频率一般越来越接近概率 B． 若随机事件发生的概率为，则 C． 互斥事件不一定是对立事件，但是对立事件一定是互斥事件 D．张奖券中有一张有奖，甲先抽，乙后抽，那么乙与甲抽到有奖奖券的可能性相同 ‎2．从三件正品、一件次品中随机取出两件，则取出的产品全是正品的概率是（ ）‎ A． B． C． D．无法确定 ‎3．有五条线段长度分别为，从这条线段中任取条，则所取条线段能构成一个三角形的概率为（ ）‎ A． B． C． D．‎ ‎4．从个同类产品（其中个是正品，个是次品）中任意抽取个的必然事件是（ ）‎ A.个都是正品 B.至少有个是次品　 C.个都是次品 D.至少有个是正品 ‎5．某产品分为甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为,出现丙级品的概率为,则对产品抽查一次抽得正品的概率是( )‎ A． B． C． D．‎ ‎6．从一批羽毛球产品中任取一个，其质量小于的概率为，质量小于的概率为，那么质量在(g)范围内的概率是（ ）‎ A． B． C． D．‎ 二、填空题 ‎1．有一种电子产品，它可以正常使用的概率为，则它不能正常使用的概率是 。‎ ‎2．一个三位数字的密码键,每位上的数字都在到这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为___‎ ‎3．同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是 。‎ ‎4．从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是 。‎ ‎5．在张卡片上分别写有数字然后将它们混合,再任意排列成一行,则得到的数能被或 整除的概率是 。‎ 三、解答题 ‎1．从甲、乙、丙、丁四个人中选两名代表，求：‎ ‎（１）甲被选中的概率 （２）丁没被选中的概率 ‎2．现有一批产品共有件，其中件为正品，件为次品：‎ ‎（1）如果从中取出一件，然后放回，再取一件，求连续次取出的都是正品的概率；‎ ‎（2）如果从中一次取件，求件都是正品的概率．‎ ‎3．某路公共汽车分钟一班准时到达某车站，求任一人在该车站等车时间少于分钟的概率（假定车到来后每人都能上）．‎ ‎4．一个路口的红绿灯,红灯的时间为秒,黄灯的时间为秒,绿灯的时间为秒,当你到达路口时看见下列三种情况的概率各是多少?‎ ‎(1) 红灯 (2) 黄灯 (3) 不是红灯 ‎《必修3》第三章：概率 ‎[综合训练B组]‎ 一、选择题 ‎1．同时向上抛个铜板，落地时个铜板朝上的面都相同，你认为对这个铜板下面情况更可能正确的是（　　）‎ Ａ．这个铜板两面是一样的 Ｂ．这个铜板两面是不同的 Ｃ．这个铜板中有个两面是一样的，另外个两面是不相同的 Ｄ．这个铜板中有个两面是一样的，另外个两面是不相同的 ‎2．口袋内装有一些大小相同的红球、白球和黒球，从中摸出个球，摸出红球的概率是，摸出白球的概率是，那么摸出黒球的概率是（ ）‎ A． B． C． D． ‎ ‎3．从装有个红球和个黒球的口袋内任取个球，那么互斥而不对立的两个事件是（ ）‎ A．至少有一个黒球与都是黒球 B．至少有一个黒球与都是黒球 ‎ C．至少有一个黒球与至少有个红球 D．恰有个黒球与恰有个黒球 ‎4．在根纤维中,有根的长度超过,从中任取一根,取到长度超过的纤维的概率是( )‎ A． B． C． D．以上都不对 ‎5．先后抛掷骰子三次，则至少一次正面朝上的概率是（ ）‎ A． B． C． D． ‎ ‎6．设为两个事件，且，则当（ ）时一定有 A．与互斥 B．与对立　　 Ｃ．　 Ｄ．不包含 二、填空题 ‎1．在件产品中，有件一级品，件二级品，则下列事件：①在这件产品中任意选出件，全部是一级品；②在这件产品中任意选出件，全部是二级品；③在这件产品中任意选出件，不全是一级品；④在这件产品中任意选出件，其中不是一级品的件数小于，其中　　　　　是必然事件；　　　　　　是不可能事件；　　　　　　是随机事件。‎ ‎2．投掷红、蓝两颗均匀的骰子，观察出现的点数，至多一颗骰子出现偶数点的概率是_____。‎ ‎3．在区间中随机地取出两个数，则两数之和小于的概率是______________。‎ ‎4．在的水中有一个草履虫,现从中随机取出水样放到显微镜下观察,则发现草履虫的概率是 ‎ 三、解答题 ‎1．袋中有大小相同的红、黄两种颜色的球各个，从中任取只，有放回地抽取次．求：‎ ① 只全是红球的概率； ② 只颜色全相同的概率； ③ 只颜色不全相同的概率．‎ ‎2．抛掷颗质地均匀的骰子，求点数和为的概率。‎ ‎3．从名男生和名女生中任选人参加演讲比赛,‎ ‎①求所选人都是男生的概率;②求所选人恰有名女生的概率;③求所选人中至少有名女生的概率。‎ ‎4．平面上画了一些彼此相距的平行线，把一枚半径的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率．‎ 新课程高中数学训练题组《必修3》参考答案 ‎《必修3》第一章 算法初步 [基础训练A组]‎ 一、选择题 ‎ ‎1.C 算法的特点：有穷性，确定性，顺序性与正确性，不唯一性，普遍性 ‎2.D 任何一个算法都有顺序结构，循环结构一定包含条件结构，二分法用到循环结构 ‎3.B 先把的值赋给中间变量，这样，再把的值赋给变量，这样，把的值赋给变量，这样 ‎4.B 把赋给变量，把赋给变量，把赋给变量，把赋给变量，输出 ‎5.D 该程序揭示的是分段函数的对应法则 二、填空题 ‎1. INPUT，WHILE，WEND 2. 注意是从大到小 ‎3. 来自课本上的思考题：一元次多项式问题 ‎4. ①，②，③，④，⑥ 基本算法语句的种类 ‎5. ， ，末位是第一个余数，注意：余数自下而上排列 三、解答题 1. 解：‎ ‎ ‎ 2. 解：‎ ‎ ‎ 3. 解： ‎ ‎ ‎ 4. 解： ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎《必修3》第一章 算法初步 [综合训练B组]‎ 一、选择题 ‎ ‎1.D ‎ ‎ 是和的最大公约数，也就是和的最大公约数 ‎2.C ‎ ‎3.B 先比较与，得；把插入到，得；把插入到，得；‎ ‎4.A 见课本赋值语句相关部分 ‎5.D Until标志着直到型循环，直到终止条件成就为止 ‎6.B 经过第一趟得；经过第二趟得；经过第三趟得 ‎；经过第四趟得；经过第五趟得；‎ 二、填空题 ‎1.（1）（2）‎ ‎2. ‎ ‎3. 、 、‎ ‎ 、 ‎ ‎4.‎ ‎5. ①; ②;‎ ‎324=243×1＋81 ‎ ‎243=81×3＋0 ‎ 则324与243的最大公约数为81 ‎ 又135=81×1＋54 ‎ ‎81=54×1＋27 ‎ ‎54=27×2＋0‎ 则81与135的最大公约数为27 ‎ 所以,三个数 324、243、135的 最大公约数为 27.‎ 另法 为所求。‎ 第3题 ‎③;④‎ 三、解答题 INPUT “x=”;x IF x>=0 and x<=4 THEN ‎ y=2x ELSE IF x<=8 THEN ‎ y=8‎ ELSE y=2*(12-x)‎ END IF END IF PRINT y END 第2题 i=1‎ sum=0‎ WHILE i<=100‎ sum=sum+i i=i+1‎ WEND PRINT sum END 第1题 ‎1.解： 2.解： 3.解：‎ 开始 输出F 结束 I≤12‎ I=3‎ S=1 Q=1‎ N Y I=I+1‎ Q=S S=F F=S+Q ‎4. 解: 根据题意可知,第一个月有对小兔,第二个 月有对成年兔子,第三个月有两对兔子,从第三个 月开始,每个月的兔子对数是前面两个月兔子对数 的和,设第个月有对兔子,第S=1‎ Q=1‎ I=3‎ WHILE I<=12‎ ‎ F=S+Q ‎ Q=S ‎ S=F ‎ I=I+1‎ WEND PRINT F END 第4题 个月有对 兔子,第个月有对兔子,则有,‎ 一个月后,即第个月时,式中变量的新值应 变第个月兔子的对数(的旧值),变量的新 值应变为第个月兔子的对数(的旧值),这 样,用求出变量的新值就是个月兔 子的数,依此类推,可以得到一个数序列,数序列的 第项就是年底应有兔子对数,我们可以先确定 前两个月的兔子对数均为,以此为基准,构造一个 循环程序,让表示“第×个月的从逐次增加,‎ 一直变化到,最后一次循环得到的就是所求 结果. 流程图和程序如右:‎ ‎《必修3》第一章 算法初步 [提高训练C组]‎ 一、选择题 ‎ ‎1.B 赋值语句的功能 ‎2.A 仅②不需要分情况讨论，即不需要用条件语句 ‎3.D ‎ ‎4.A ①;②‎ ‎5.D ‎ ‎6.B 经过一趟得:;经过二趟得:;经过三趟得:‎ 二、填空题 ‎1. ‎ ‎2. ‎ ‎3. 4.将按从大到小的顺序排列后再输出 三、解答题 1. 解： 第一步：取 第二步：计算 第三步：计算 第四步：输出的值 ‎2.解：算法如下：‎ ‎1、 取中点，将区间一分为二 ‎2、 若，则就是方程的根；否则所求根在的左侧或右侧 若，则，以代替；‎ ‎ 若，则，以代替；‎ ‎3、若，计算终止 此时，否则转到第1步 算法语句： 流程图：‎ Input ‎ repeat if ‎ then print ‎ else if ‎ then ‎ else ‎ until ‎ print ‎ end ‎ ‎ ‎《必修3》第二章 统计 [基础训练A组]‎ 一、选择题 ‎ ‎1.D 总和为；样本数据分布最广，即频率最大，为众数，；‎ ‎ 从小到大排列，中间一位，或中间二位的平均数，即 ‎2.B 平均数不大于最大值，不小于最小值 ‎3.B 少输入平均数少，求出的平均数减去实际的平均数等于 ‎4.D ‎ ‎5.B ，间隔应为 ‎6.A 频数为；频率为 二、填空题 ‎1.④，⑤，⑥ 名运动员的年龄情况是总体；每个运动员的年龄是个体；‎ ‎2. 位执“一般”对应位“不喜欢”，即“一般”是“不喜欢”的倍，而他们的差为人，即“一般”有人，“不喜欢”的有人，且“喜欢”是“不喜欢”的倍，即人，全班有人，‎ ‎3. ‎ ‎4．（1），（2），‎ ‎ （1）‎ ‎（2）‎ ‎5. 频率/组距，组距，频率 三、解答题 ‎1.解：‎ ‎2.解：（1） ‎ ‎ （2）…（3）在范围内最多。‎ ‎3.解：从高三年级抽取的学生人数为 ‎ 而抽取的比例为，高中部共有的学生为 甲班 乙班 ‎2‎ ‎5‎ ‎8 6‎ ‎6‎ ‎2‎ ‎8 6 6 4 2‎ ‎7‎ ‎4 6 8‎ ‎2‎ ‎8‎ ‎2 4 5 6 8‎ ‎6‎ ‎9‎ ‎2‎ ‎4.解：‎ 乙班级总体成绩优于甲班。‎ ‎《必修3》第二章 统计 [综合训练B组]‎ 一、选择题 ‎ ‎1.D ‎ ‎2.D ③的间隔为,可为系统抽样;④的第一个数为,不符合系统抽样,因为间隔为,④的第一个数应该为;分层抽样则要求初一年级应该抽取人,号码在,所以④中的不符合分层抽样 ‎3.C ［25，25.9］包括［25，25.3］，6；［25.3，25.6］，4；［25.6，25.9］，10；频数之和为，频率为 ‎4.C ‎5.D ，‎ 二、填空题 ‎1. ，，‎ ‎2． ‎ ‎3. 每个个体被抽取的机率都是 ‎ ‎4. ‎ ‎5． 总人数为 三、解答题 ‎1. 解：, ‎ ‎,‎ ‎∵ ∴ 甲的平均成绩较好，乙的各门功课发展较平衡 ‎2. 解：而抽取的比例为，在不到岁的教师中应抽取的人数为 ‎3. 解：在的汽车的频率为，在的汽车有 ‎《必修3》第二章 统计 [提高训练C组]‎ 一、选择题 ‎ ‎1.B 抽取的比例为 ‎2.C 剔除零头 ‎3.D 间隔为 4.C 5.C 见课本相关内容 二、填空题 ‎1. 函数关系是两个变量之间有完全确定的关系，而相关关系是两个变量之间并没有严格的确定关系，当一个变量变化时，另一变量的取值有一定的随机性。‎ ‎2. ‎ ‎3.简单随机抽样 总体个数较少 ‎4. 不论先后，被抽取的概率都是 ‎5．甲比乙稳定 甲稳定性强 三、解答题 ‎1. 解：（1）频率为：，频数：‎ ‎（2）‎ ‎2. 解：（1）数据对应的散点图如图所示：‎ ‎ ‎ ‎（2），，‎ 设所求回归直线方程为，‎ 则 故所求回归直线方程为 ‎（3）据（2），当时，销售价格的估计值为：‎ ‎（万元）‎ ‎《必修3》第三章 概率 [基础训练A组]‎ 一、选择题 ‎ ‎1.A 频率所稳定在某个常数上，这个常数叫做概率，‎ ‎2.B ‎ ‎3.B 能构成三角形的边长为三种，‎ ‎4.D 至少有一件正品 5.D ‎ ‎6.C ‎ 二、填空题 ‎1. ‎ ‎2. ‎ ‎3. ‎ ‎4. ‎ ‎5. ，或者：个位总的来说有种情况，符合条件的有种 三、解答题 ‎1. 解：（1）记甲被选中为事件，则 ‎ （2）记丁被选中为事件，则 ‎2. 解：（1）有放回地抽取次，按抽取顺序记录结果，则都有种可能，所以试验结果有种；设事件为“连续次都取正品”，则包含的基本事件共有种，因此，‎ ‎（2）可以看作不放回抽样次，顺序不同，基本事件不同，按抽取顺序记录，则有种可能，有种可能，有种可能，所以试验的所有结果为种．设事件为“件都是正品”，则事件包含的基本事件总数为, 所以 ‎ ‎3. 解：可以认为人在任何时刻到站是等可能的。设上一班车离站时刻为，则该人到站的时刻的一切可能为，若在该车站等车时间少于分钟，则到站的时刻为，。‎ ‎4. 解：总的时间长度为秒，设红灯为事件，黄灯为事件，‎ ‎（1）出现红灯的概率 ‎（2）出现黄灯的概率 ‎（3）不是红灯的概率 ‎ ‎ ‎《必修3》第三章 概率 [综合训练B组]‎ 一、选择题 ‎ ‎1.A 假设正反两面是不同的，则相同的面次都朝上的概率为 这个概率太小了，几乎是不可能事件 ‎2.C ‎ ‎3.D 4. B 在根纤维中，有根的长度超过，即基本事件总数为，且它们是等可能发生的，所求事件包含个基本事件，故所求事件的概率为 ‎5.D 至少一次正面朝上的对立事件的概率为 ‎6.B 对立事件 二、填空题 ‎1.③,④; ②; ① 2. 其对立事件为都出现奇数点，‎ ‎3. 4. ‎ 三、解答题 ‎1.解：①每次抽到红球的概率为 ②每次抽到红球或黄球 ③颜色不全相同是全相同的对立，‎ ‎2. 解：在抛掷颗骰子的试验中，每颗骰子均可出现点，点，…，点种不同的结果，我们把两颗骰子标上记号以便区分，因此同时掷两颗骰子的结果共有，在上面的所有结果中，向上的点数之和为的结果有，共种，所以，所求事件的概率为.‎ ‎3.解：基本事件的总数为 ‎ ①所选人都是男生的事件数为 ‎ ②所选人恰有女生的事件数为 ‎ ‎2a r o M ③所选人恰有女生的事件数为 所选人中至少有名女生的概率为 ‎4. 解：把“硬币不与任一条平行线相碰”的事件记为事件，为了确定硬币的位置，由硬币中心向靠得最近的平行线引垂线，垂足为，如图所示，这样线段长度（记作）的取值范围就是，只有当时硬币不与平行线相碰，所以所求事件的概率就是 ‎=‎