2014-2018年五年真题分类第五章 平面向量

2014-2018年五年真题分类第五章 平面向量

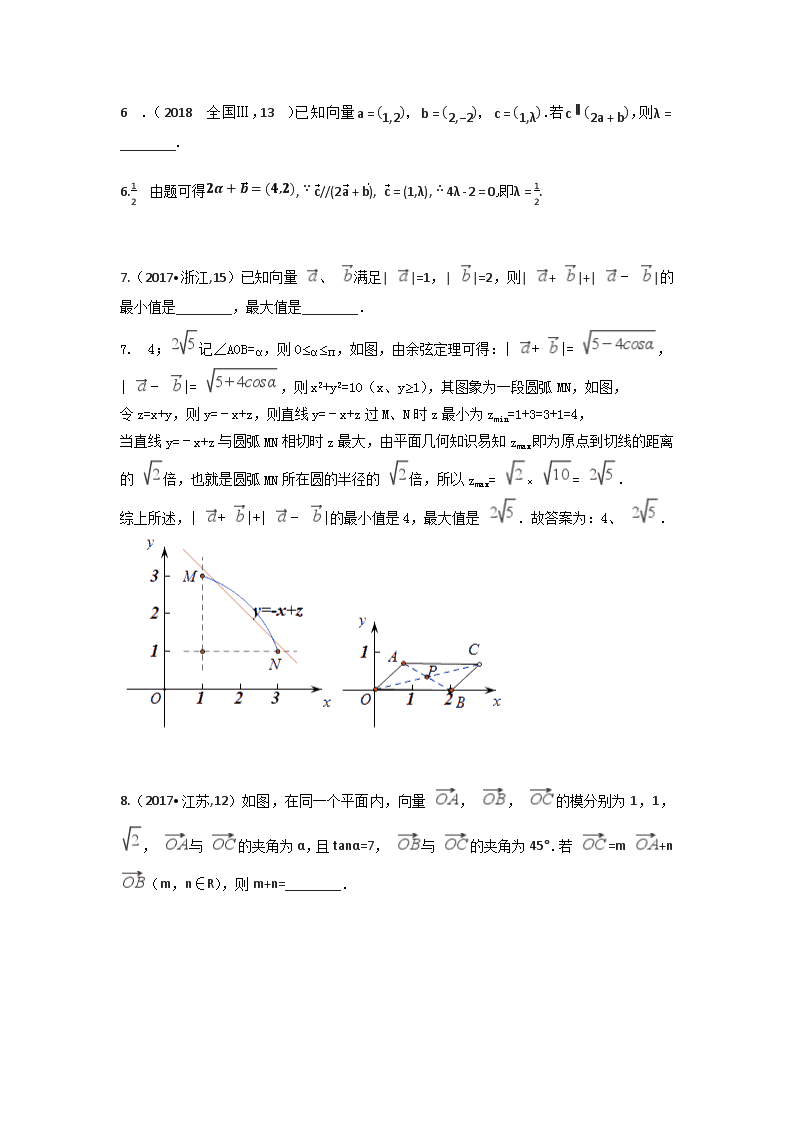
第五章 平面向量 考点1 平面向量的概念及坐标运算 ‎1．（2018全国Ⅰ，6）在△ABC中，AD为BC边上的中线，E为AD的中点，则EB‎=‎(　　)‎ A．‎3‎‎4‎AB‎−‎‎1‎‎4‎AC B．‎‎1‎‎4‎AB‎−‎‎3‎‎4‎AC C．‎3‎‎4‎AB‎+‎‎1‎‎4‎AC D．‎‎1‎‎4‎AB‎+‎‎3‎‎4‎AC ‎1.A 根据向量的运算法则，可得 BE‎=‎1‎‎2‎BA+‎1‎‎2‎BD=‎1‎‎2‎BA+‎1‎‎4‎BC=‎1‎‎2‎BA+‎1‎‎4‎(BA+AC)‎‎ ‎=‎1‎‎2‎BA+‎1‎‎4‎BA+‎1‎‎4‎AC=‎3‎‎4‎BA+‎‎1‎‎4‎AC，‎ 所以EB‎=‎3‎‎4‎AB-‎‎1‎‎4‎AC，故选A.‎ ‎2.(2015·新课标全国Ⅰ，7)设D为△ABC所在平面内一点，＝3，则(　　)‎ A.＝－＋ B.＝－ C.＝＋ D.＝－ ‎2.A[∵＝3，∴－＝3(－)，即4－＝3，‎ ‎∴＝－＋.]‎ ‎3.(2015·湖南，8)已知点A，B，C在圆x2＋y2＝1上运动，且AB⊥BC.若点P的坐标为(2,0)，则|＋＋|的最大值为(　　)‎ A.6 B.7 C.8 D.9‎ ‎3.B　[由A,B,C在圆x2＋y2＝1上,且AB⊥BC,∴AC为圆直径,故＋＝2＝(－4，0),设B(‎ x，y)，则x2＋y2＝1且x∈[-1,1]，＝(x－2，y)，所以＋＋＝(x-6，y).故|＋＋|＝，∴x＝－1时有最大值＝7，故选B.]‎ ‎4.(2014·福建，8)在下列向量组中，可以把向量a＝(3,2)表示出来的是(　　)‎ A.e1＝(0,0)，e2＝(1,2) B.e1＝(－1,2)，e2＝(5，－2)‎ C.e1＝(3,5)，e2＝(6,10) D.e1＝(2，－3)，e2＝(－2,3)‎ ‎4.B　[法一　若e1＝(0，0)，e2＝(1，2)，则e1∥e2，而a不能由e1，e2表示，排除A；若e1＝(－1，2)，e2＝(5，－2)，因为≠，所以e1，e2不共线，根据共面向量的基本定理，可以把向量a＝(3，2)表示出来，故选B.‎ 法二　因为a＝(3，2)，若e1＝(0，0)，e2＝(1，2)，不存在实数λ，μ，使得a＝λe1＋μe2，排除A；若e1＝(－1，2)，e2＝(5，－2)，设存在实数λ，μ，使得a＝λe1＋μe2，则(3，2)＝(－λ＋5μ，2λ－2μ)，‎ 所以解得所以a＝2e1＋e2，故选B.]‎ ‎5.(2014·安徽，10)在平面直角坐标系xOy中，已知向量a，b，|a|＝|b|＝1，a·b＝0，点Q满足＝(a＋b).曲线C＝{P|＝acosθ＋bcosθ，0≤θ<2π}，区域Ω＝{P|0|≤|a||b|恒成立；对于B，当a，b均为非零向量且方向相反时不成立；对于C、D容易判断恒成立.故选B.]‎ ‎18.(2014·新课标全国Ⅱ，3)设向量a，b满足|a＋b|＝，|a－b|＝，则a·b＝(　　)‎ A.1 B.2 C.3 D.5‎ ‎18.A　[由向量的数量积运算可知,∵|a＋b|＝,∴(a＋b)2＝10,∴a2+b2+2a·b＝10,①‎ 同理a2＋b2－2a·b＝6，②‎ ① ‎－②得4a·b＝4，∴a·b＝1.]‎ ‎19.(2014·大纲全国，4)若向量a、b满足：|a|＝1，(a＋b)⊥a，(2a＋b)⊥b，则|b|＝(　　)‎ A.2 B. C.1 D. ‎19.B　[由题意得⇒-2a2+b2＝0,即－2|a|2＋|b|2＝0,又|a|＝1，‎ ‎∴|b|＝.故选B.]‎ ‎20.(2014·天津，8)已知菱形ABCD的边长为2，∠BAD＝120°，点E，F分别在边BC，DC上，BE＝λBC，DF＝μDC.若·＝1，·＝－，则λ＋μ＝(　　)‎ A. B. C. D. ‎20.C　[如图所示,以菱形ABCD的两条对角线所在直线为坐标轴,建立平面直角坐标系xOy,不妨设A(0，－1),B(－，0),C(0，1),D(，0),由题意得＝(1－λ)·＝(λ－，λ－1)，＝(1－μ)＝(－μ，μ－1).‎ 因为·＝-，所以3(λ-1)·(1-μ)＋(λ-1)(μ-1)＝－，即(λ-1)(μ-1)＝.‎ 因为＝＋＝(λ－，λ＋1).＝＋＝(－μ，μ＋1)，‎ 又·＝1，所以(λ＋1)(μ＋1)＝2.由整理得λ＋μ＝.选C.]‎ ‎21.（2017•新课标Ⅰ,13）已知向量 ， 的夹角为60°，| |=2，| |=1，则| +2 |=________． ‎ ‎21. ∵向量 ， 的夹角为60°，且| |=2，| |=1， ∴ = +4 • +4 =22+4×2×1×cos60°+4×12 =12， ∴| +2 |=2 ．故答案为：2 ． ‎ ‎22.（2017•山东,12）已知 ，  是互相垂直的单位向量，若 ﹣   与 +λ 的夹角为60°，则实数λ的值是________． ‎ ‎22. ，  是互相垂直的单位向量，∴| |=| |=1，且 • =0； 又 ﹣   与 +λ 的夹角为60°，∴（ ﹣ ）•（ +λ ）=| ﹣ |×| +λ |×cos60°，即 +（ ﹣1） • ﹣λ = × × ，化简得 ﹣λ= × × ，即 ﹣λ= ，解得λ= ．故答案为： ． 23.（2017·天津,13）在△ABC中，∠A=60°，AB=3，AC=2．若 =2 ， =λ ﹣ （λ∈R），且 =﹣4，则λ的值为________． ‎ ‎23. 如图所示， ‎ ‎ △ABC中，∠A=60°，AB=3，AC=2， =2 ， ∴ = + = + = + （ ﹣ ） = + ， 又 =λ ﹣ （λ∈R）， ∴ =（ + ）•（λ ﹣ ） =（ λ﹣ ） • ﹣ + λ =（ λ﹣ ）×3×2×cos60°﹣ ×32+ λ×22=﹣4， ∴ λ=1， 解得λ= ．故答案为： ． ‎ ‎24.(2016·浙江，15)已知向量a，b，|a|＝1，|b|＝2.若对任意单位向量e，均有|a·e|＋|b·e|≤，则a·b的最大值是________.‎ ‎24. [由已知可得：≥|a·e|＋|b·e|≥|a·e＋b·e|＝|(a＋b)·e|‎ 由于上式对任意单位向量e都成立.∴≥|a＋b|成立.‎ ‎∴6≥(a＋b)2＝a2＋b2＋2a·b＝12＋22＋2a·b.即6≥5＋2a·b，∴a·b≤.]‎ ‎25.(2015·天津，14)在等腰梯形ABCD中，已知AB∥DC，AB＝2，BC＝1，∠ABC ‎＝60°，动点E和F分别在线段BC和DC上，且＝λ，＝，则||·||的最小值为________.‎ ‎25.　[在梯形ABCD中，AB＝2，BC＝1，∠ABC＝60°，可得DC＝1，＝＋λ，＝＋，∴·＝(＋λ)·(＋)＝·＋·＋λ·＋λ·＝2×1×cos 60°＋2×＋λ×1×cos 60°＋λ×cos 120°＝＋＋≥2＋＝，当且仅当＝，即λ＝时，取得最小值为.]‎ ‎26.(2015·浙江，15)已知e1,e2是空间单位向量,e1·e2＝，若空间向量b满足b·e1＝2，b·e2＝，且对于任意x，y∈R，|b－(xe1＋ye2)|≥|b－(x0e1＋y0e2)|＝1(x0，y0∈R)，则x0＝________，y0＝________，|b|＝________.‎ ‎26.1　2　2　[∵e1·e2＝|e1|·|e2|cos〈e1，e2〉＝，∴〈e1，e2〉＝.不妨设e1＝，e2＝(1，0，0)，b＝(m，n，t).‎ 由题意知解得n＝，m＝，∴b＝.‎ ‎∵b－(xe1＋ye2)＝，‎ ‎∴|b－(xe1＋ye2)|2＝＋＋t2＝x2＋xy＋y2－4x－5y＋t2＋7＝＋(y－2)2＋t2.由题意知，当x＝x0＝1，y＝y0＝2时，＋(y－2)2＋t2取到最小值.此时t2＝1，‎ 故|b|＝＝2.]‎ ‎27.（2017•江苏,16）已知向量 =（cosx，sinx）， =（3，﹣ ），x∈[0，π]． ‎ ‎（Ⅰ）若 ∥ ，求x的值； （Ⅱ）记f（x）= ，求f（x）的最大值和最小值以及对应的x的值． ‎ ‎27.（Ⅰ）∵ =（cosx，sinx）， =（3，﹣ ）， ∥ ， ∴﹣ cosx+3sinx=0， ∴tanx= ， ∵x∈[0，π]， ∴x= ，‎ ‎（Ⅱ）f（x）= =3cosx﹣ sinx=2 （ cosx﹣ sinx）=2 cos（x+ ）， ∵x∈[0，π]，∴x+ ∈[ ， ]，∴﹣1≤cos（x+ ）≤ ， 当x=0时，f（x）有最大值，最大值3，当x= 时，f（x）有最小值，最大值﹣2 28.(2015·广东，16)在平面直角坐标系xOy中,已知向量m＝,n＝(sin x，cos x)，x∈.‎ ‎(1)若m⊥n，求tan x的值.‎ ‎(2)若m与n的夹角为，求x的值.‎ ‎28.解　(1)因为m＝，n＝(sin x，cos x)，m⊥n.‎ 所以m·n＝0，即sin x－cos x＝0，所以sin x＝cos x，所以tan x＝1.‎ ‎(2)因为|m|＝|n|＝1,所以m·n＝cos＝，即sin x－cos x＝，所以sin＝，‎ 因为0

查看更多