2020届二轮复习　解三角形课件（全国通用）

2020届二轮复习　解三角形课件（全国通用）

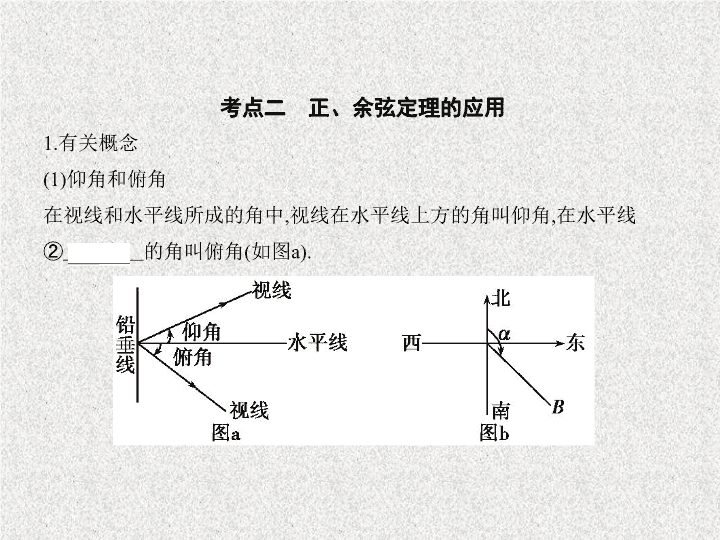
§4.5 解三角形 高考理数 考点一　正弦定理和余弦定理 知识清单 考点二　正、余弦定理的应用 1.有关概念 (1)仰角和俯角 在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线 ② 　下方     的角叫俯角(如图a).   (2) 方位角 从指北方向顺时针转到目标方向线的水平角叫方位角 , 如 B 点的方位角 为 α ( 如图 b). (3) 方向角 : 相对于某一正方向的水平角 ( 如图 c). a. 北偏东 α ° : 指北方向③ 　顺时针     旋转 α ° 到达目标方向 . b. 东北方向 : 指北偏东 45 ° .   (4)坡角:④ 　坡面     与水平面所成的锐二面角叫坡角(如图d,角 θ 为坡角). 坡度:坡面的铅直高度与⑤ 　水平宽度     之比叫做坡度(或坡比)(如图d, i 为坡比).   2.三角形的面积公式 设△ ABC 的三边为 a , b , c ,三边所对的三个角分别为 A , B , C ,面积为 S . (1) S =   ah ( h 表示边 BC 上的高). (2) S =   ab sin C =   ac sin B =   bc sin A . (3) S =   =2 R 2 sin A sin B sin C ( R 为△ ABC 外接圆的半径). (4) S =   r ( a + b + c )( r 为△ ABC 内切圆的半径). (5) S =     . 3.解斜三角形在实际中的应用 解斜三角形在实际中的应用非常广泛,如测量、航海等方面都可能用到.解题的一般步骤: (1)分析题意,准确理解题意,分清已知与所求; (2)根据题意画出示意图; (3)将需要求解的问题归结到一个或几个三角形中,通过合理运用正弦 定理、余弦定理等有关知识求解; (4)检验所得的结果是否具有实际意义,对解进行取舍,并写出答案. 1.已知两角 A 、 B 与一边 a ,由 A + B + C =π及   =   =   ,可先求出角 C , 再求出 b 、 c . 2.已知两边 b 、 c 及其夹角 A ,由 a 2 = b 2 + c 2 -2 bc cos A ,先求出 a ,再由正弦定理 求出角 B 、 C . 3.已知三边 a 、 b 、 c ,由余弦定理可求出角 A 、 B 、 C . 解三角形的常见题型及求解方法 方法 1 方法技巧 4.已知两边 a 、 b 及其中一边 a 的对角 A ,由正弦定理   =   可求出另 一边 b 的对角 B ,由 C =π-( A + B )可求出 C ,再由   =   可求出 c ,而通过   =   求 B 时,可能有一解,两解或无解的情况,其判断方法如下表: 例 1    (2017 课标全国 Ⅲ,17,12 分 )△ ABC 的内角 A , B , C 的对边分别为 a , b , c . 已知 sin A +   cos A =0, a =2   , b =2. (1) 求 c ; (2) 设 D 为 BC 边上一点 , 且 AD ⊥ AC , 求△ ABD 的面积 . 解题导引 解析　 (1) 由已知可得 tan A =-   , 所以 A =   . 在△ ABC 中 , 由余弦定理得 28=4+ c 2 -4 c cos   , 即 c 2 +2 c -24=0. 解得 c =-6( 舍去 ), 或 c =4. (2) 由题设可得∠ CAD =   , 所以∠ BAD =∠ BAC -∠ CAD =   . 故△ ABD 面积与△ ACD 面积的比值为   =1. 又△ ABC 的面积为   × 4 × 2sin∠ BAC =2   , 所以△ ABD 的面积为   . 一题多解     (2) 另解一 : 由余弦定理得 cos C =   , 在 Rt△ ACD 中 ,cos C =   ,∴ CD =   , ∴ AD =   , DB = CD =   , ∴ S △ ABD = S △ ACD =   × 2 ×   × sin C =   ×   =   . 另解二 :∠ BAD =   , 由余弦定理得 cos C =   ,∴ CD =   ,∴ AD =   ,∴ S △ ABD =   × 4 ×   × sin∠ DAB =   . 另解三 : 过 B 作 BE 垂直 AD , 交 AD 的延长线于 E , 在△ ABE 中 ,∠ EAB =   -   =   , AB =4,∴ BE =2,∴ BE = CA , 从而可得△ ADC ≌△ EDB ,∴ BD = DC , 即 D 为 BC 中点 ,∴ S △ ABD =   S △ ABC =   ×   × 2 × 4 × sin∠ CAB =   . 在判断三角形的形状时,一般将已知条件中的边角关系利用正弦定理或 余弦定理转化为角与角之间的关系或边与边之间的关系,再用三角变换 或代数式的恒等变形(如因式分解法、配方法等)求解,注意等式两边的 公因式不要约掉,要移项提取公因式,否则会有漏掉一种形状的可能. 例2    在△ ABC 中, a 、 b 、 c 分别表示三个内角 A 、 B 、 C 的对边,如果( a 2 + b 2 )sin( A - B )=( a 2 - b 2 )sin( A + B ),判断三角形的形状. 利用正、余弦定理判断三角形的形状 方法 1 解题导引 解析　解法一:已知等式可化为 a 2 [sin( A - B )-sin( A + B )]= b 2 [-sin( A + B )-sin( A - B )], ∴2 a 2 cos A sin B =2 b 2 cos B sin A . 由正弦定理可知上式可化为 sin 2 A cos A sin B =sin 2 B cos B sin A , ∴sin A sin B (sin A cos A -sin B cos B )=0, ∴sin 2 A =sin 2 B ,由0<2 A <2π,0<2 B <2π, 得2 A =2 B 或2 A =π-2 B , 即 A = B 或 A =   - B , ∴△ ABC 为等腰三角形或直角三角形. 解法二:同解法一可得2 a 2 cos A sin B =2 b 2 sin A cos B . 由正、余弦定理,可得 a 2 b ·   = b 2 a ·   , ∴ a 2 ( b 2 + c 2 - a 2 )= b 2 ( a 2 + c 2 - b 2 ), 即( a 2 - b 2 )( a 2 + b 2 - c 2 )=0, ∴ a = b 或 a 2 + b 2 = c 2 , ∴△ ABC 为等腰三角形或直角三角形. 评析    判断三角形形状可通过边和角两种途径进行判断,应根据题目条件选用合适的策略: (1)若用边的关系,则有:若 A 为锐角,则 b 2 + c 2 - a 2 >0;若 A 为直角,则 b 2 + c 2 - a 2 =0;若 A 为钝角,则 b 2 + c 2 - a 2 <0. (2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角恒等变换得出内角的关系,从而判断出三角形的形状,此时要注意应用 A + B + C =π这个结论. 1.几种常见题型 测量距离问题、测量高度问题、测量角度问题、计算面积问题、航海 问题、物理问题等. 2.解题时需注意的几个问题 (1)要注意仰角、俯角、方位(向)角等名词,并能准确地找出这些角; (2)要注意将平面几何中的性质、定理与正、余弦定理结合起来,发现 题目中的隐含条件. 正、余弦定理的实际应用策略 方法 3 3. 解三角形应用题的方法 (1) 解三角形应用题的一般步骤 (2) 解三角形应用题的两种情形 ①实际问题经抽象概括后 , 已知量与未知量全部集中在一个三角形中 , 可用正弦定理或余弦定理求解 . ② 实际问题经抽象概括后 , 已知量与未知量涉及两个 ( 或两个以上 ) 三角 形 , 这时需作出这些三角形 , 先解够条件的三角形 , 然后逐步求出其他三 角形中的解 , 有时需设出未知量 , 从几个三角形中列出方程 , 解方程得出 所要求的解 . (3) 解三角形应用题应注意的问题 ①画出示意图后要注意寻找一些特殊三角形 , 如等边三角形、直角三角 形等 , 这样可以优化解题过程 . ② 解三角形时 , 为避免误差的积累 , 应尽可能用已知的数据 ( 原始数据 ), 少用间接求出的量 . 例 3    (2017 河南六市联考 ,18) 某地棚户区改造建筑用地的平面示意图 如图所示 , 经规划调研确定 , 棚改规划建筑用地区域近似为圆面 , 该圆面 的内接四边形 ABCD 是原棚户区建筑用地 , 测量 可知边界 AB = AD =4 万米, BC =6万米, CD =2万米. (1)请计算原棚户区建筑用地 ABCD 的面 积及 AC 的长; (2)因地理条件的限制,边界 AD , DC 不能变更,而边界 AB , BC 可以调整,为 了提高棚户区建筑用地的利用率,请在弧   上设计一点,使得棚户区 改造后的新建筑用地 APCD 的面积最大,并求出最大值. 解题导引 解析　 (1) 根据题意知 , 四边形 ABCD 内接于圆 , ∴∠ ABC +∠ ADC =π. 在△ ABC 中 , 由余弦定理得 AC 2 = AB 2 + BC 2 -2 AB · BC ·cos∠ ABC , 即 AC 2 =4 2 + 6 2 -2 × 4 × 6 × cos∠ ABC . 在△ ADC 中 , 由余弦定理得 AC 2 = AD 2 + DC 2 -2 AD · DC ·cos∠ ADC , 即 AC 2 =4 2 +2 2 -2 × 4 × 2 × cos∠ ADC . 又 cos∠ ADC =-cos∠ ABC , ∴cos∠ ABC =   , AC 2 =28, 即 AC =2   万米 . 又∠ ABC ∈(0,π),∴∠ ABC =   ,∠ ADC =   . ∴ S 四边形 ABCD =   × 4 × 6 × sin   +   × 2 × 4 × sin   =8   ( 万平方米 ).   (6 分 ) (2) 由题意知 , S 四边形 APCD = S △ ADC + S △ APC , 且 S △ ADC =   AD · CD ·sin   =2   ( 万平方 米 ).   (8 分 ) 设 AP = x , CP = y . ∵∠ APC =∠ ABC =   ,∴ S △ APC =   xy sin   =   xy . 在△ APC 中 , 由余弦定理得 AC 2 = x 2 + y 2 -2 xy ·cos   = x 2 + y 2 - xy =28. 又 x 2 + y 2 - xy ≥ 2 xy - xy = xy , 当且仅当 x = y 时取等号 , ∴ xy ≤ 28.   (11 分 ) ∴ S 四边形 APCD =2   +   xy ≤ 2   +   × 28=9   ( 万平方米 ), 故所求面积的最大值为 9   万平方米 , 此时点 P 为弧   的中点 .   (12 分 ) 方法点拨　本题主要考查三角形在实际生活中的应用. (1)在△ ABC 和△ ADC 中,灵活利用余弦定理求解即可. (2)设出 AP , CP 的长,在△ APC 中,结合余弦定理和基本不等式求解即可.