江苏省基地学校2021届高三上学期第一次大联考数学试题（12月）

江苏省基地学校2021届高三上学期第一次大联考数学试题（12月）

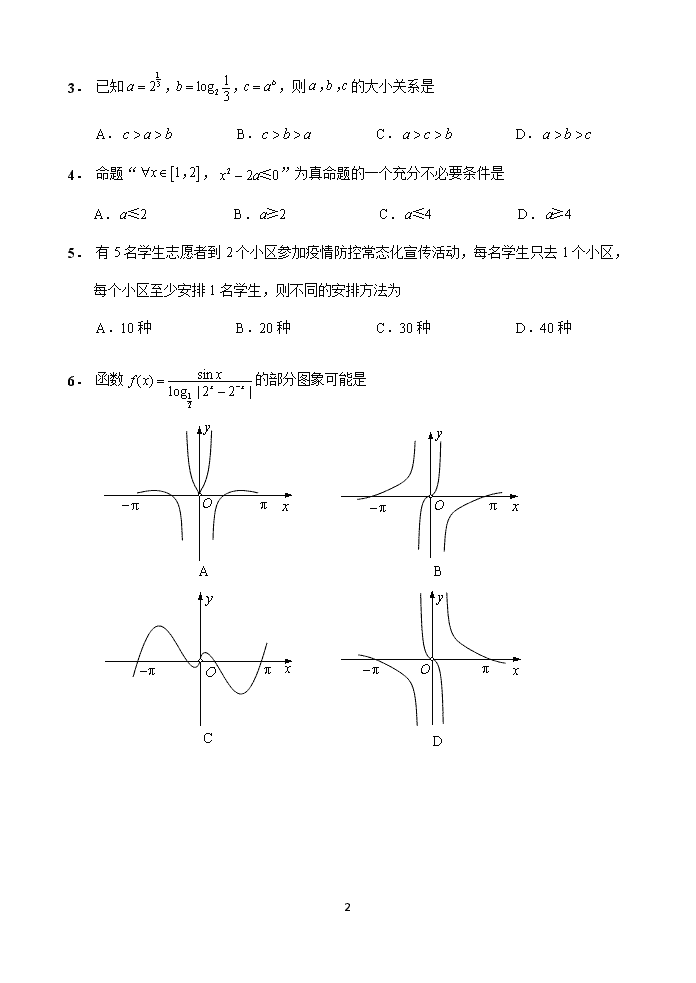
1 2021 届江苏基地学校高三第一次大联考 数 学 （考试时间：120 分钟 满分：150 分） 一、选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中，只有一项 是符合题目要求的。 1． 已知U  R ， { || | 2}A x x  ， { | 1 4}B x x    ，则 ( )U A B ð A． ( 1 2) ， B． ( 2] ， C． (2 4)， D．[2 4)， 2． 已知复数 z 的共轭复数为 z ，若 2i ( > 0)z a a  ，且 4z z  ，则 a A．1 B． 2 C．2 D． 6 3． 已知 1 3 2 12 log 3 ba b c a  ， ， ，则 a b c， ， 的大小关系是 A． c a b  B． c b a  C． a c b  D． a b c  4． 命题“  1 2x  ， ， 2 2 0x a ≤ ”为真命题的一个充分不必要条件是 A． 2a≤ B． 2a≥ C． 4a≤ D． 4a≥ 5． 有 5 名学生志愿者到 2 个小区参加疫情防控常态化宣传活动，每名学生只去 1 个小区， 每个小区至少安排 1 名学生，则不同的安排方法为 A．10 种 B．20 种 C．30 种 D．40 种 注 意 事 项 考生在答题前请认真阅读本注意事项及各题答题要求 1． 答卷前，考生务必将自己的姓名、准考证号等用 0.5 毫米黑色墨水的签字笔填写在答 题卡和试卷的指定位置上。 2． 回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑。 如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，用 0.5 毫米黑 色墨水的签字笔将答案写在答题卡上。写在本试卷上无效。 3． 考试结束后，将本试卷和答题卡一并交回。 2 6． 函数 1 2 sin( ) log | 2 2 |x x xf x   的部分图象可能是 7． 若双曲线 2 2 1 : 13 y xC a  与双曲线 22 2 : 16 9 yxC   的渐近线相同，则双曲线 1C 的离心率 为 A． 10 2 B． 15 3 C． 5 2 D． 3 3 8． 2013 年 9 月 7 日，习近平总书记在哈萨克斯坦纳扎尔巴耶夫大学发表演讲并回答学生 们提出的问题，在谈到环境保护问题时他指出：“我们既要绿水青山，也要金山银山。 宁要绿水青山，不要金山银山，而且绿水青山就是金山银山。”“绿水青山就是金山银 山”这一科学论断，成为树立生态文明观、引领中国走向绿色发展之路的理论之基。某 市为了改善当地生态环境，2014 年投入资金 160 万元，以后每年投入资金比上一年增加 20 万元，从 2020 年开始每年投入资金比上一年增加 10%，到 2024 年底该市生态环境建 设投资总额大约为 A．2655 万元 B．2970 万元 C．3005 万元 D．3040 万元 二、选择题：本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的四个选项中，有多项符 合题目要求，全部选对的得 5 分，有选错的得 0 分，部分选对的得 3 分。 A xO y π π π B xO y π C xO y π π π D x y Oπ 3 9． 2019 年 1 月到 2019 年 12 月某地新能源汽车配套公共充电桩保有量如下： 则下列说法正确的是 A．2019 年各月公共充电桩保有量一直保持增长态势 B．2019 年 12 月较 2019 年 11 月公共充电桩保有量增加超过 2 万台 C．2019 年 6 月到 2019 年 7 月，公共充电桩保有量增幅最大 D．2019 年下半年各月公共充电桩保有量均突破 45 万台 10．设 a bR， ，则下列结论正确的是 A．若 0a b  ，则 2 2 1 1 a b  B．若 0a b  ，则 2 2( 1) ( 1)a b   C．若 2a b  ，则 2 2 4a b ≥ D．若 2 1 1+2ba b a  ，则 a b 11．如图，在半圆柱中， AB 为上底面直径， DC 为下底面直径， AD BC， 为母线， AB 2AD ，点 F 在 AB 上，点G 在 DC 上， 1BF DG  ， P 为 DC 的中点．则 A． BF ∥ PG B．异面直线 AF 与CG 所成角为 60 C．三棱锥 P ACG 的体积为 3 2 D．直线 AP 与平面 ADG 所成角的正弦值为 15 10 BA CD F P G （第 11 题） 4 12．已知函数 ( ) 3 2sin sin 2f x x x   ，则下列结论正确的是 A．函数 ( )f x 是周期函数 B．函数 ( )f x 在  ， 上有 4 个零点 C．函数 ( )f x 的图象关于 ( 3)， 对称 D．函数 ( )f x 的最大值为 5 3 2 三、填空题：本题共 4 小题，每小题 5 分，共计 20 分。 13．已知向量 ( 1 )t  ，a ， (3 1) ，b ，且 (2 ) a b b ，则t  ． 14．设函数 21 2 ( ) 1 ( 2) 22      x x f x f x x ， ≤ ， ， ，则 ( (6)) f f ． 15．已知抛物线 2:C y x ，斜率为 3 2 的直线 l 经过点 (1 0)， ，且与C 交于 A B， 两点（其中 A 点在 x 轴上方）．若 B 点关于 x 轴的对称点为 P ，则 APB△ 外接圆的方程为 ． 16．某公司周年庆典活动中，制作的“水晶球”工艺品如图所示，底座是用一边长为 2 m 的 正方形钢板，按各边中点连线垂直折起四个小三角形制成，再将一个水晶玻璃球放入 其中．若水晶球最高点到底座底面的距离为 ( 2 1) m， 则水晶球的表面积为 m2． 四、解答题：本题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步骤。 17．（本小题满分 10 分） 在① 3 sin cosc A a C ，② πtan( ) 2 34C    ，③ 2 2 2 3a b c ab   这三个条件中任选 一个，补充在下面问题中，并加以解答． 已知△ABC 中的内角 A，B，C 的对边分别为 a，b，c，面积为 S ．若 4c  ， 105B   ， ，求 a 和 S ． 注：如果选择多个条件分别解答，按第一个解答计分． 18．（本小题满分 12 分） （第 16 题） 5 已知数列{ }na 的前 n 项和为 nS ，且 1n na S  ， 2 1 log n n n ab a    ， *nN ． （1）求数列{ }na ，{ }nb 的通项公式； （2）设 1 1 2 ( 2)n n n n nc b b    ，数列{ }nc 的前 n 项和为 nT ，求证： 3 1 16 4nT ≤ ． 19．（本小题满分 12 分） 近年来，我国肥胖人群的规模不断扩大，肥胖人群有很大的心血管安全隐患．目前， 国际上常用身体质量指数（Body Mass Index，缩写 BMI）来衡量人体胖瘦程度以及 是否健康，其计算公式是 2 2 kgBMI= m 体重（单位： ） 身高（单位： ）．中国成人的 BMI 数值标准为： BMI<18.5 为偏瘦；18.5≤BMI<24 为正常；24≤BMI<28 为偏胖；BMI≥28 为肥胖． 某单位随机调查了 100 名员工，测量身高、体重并计算出 BMI 值． （1）根据调查结果制作了如下 2 2 列联表，请将 2 2 列联表补充完整，并判断是否 有 99%的把握认为肥胖与不经常运动有关； 肥胖 不肥胖 合计 经常运动员工 40 60 不经常运动员工 24 40 合计 100 （2）若把上表中的频率作为概率，现随机抽取 3 人进行座谈，记抽取的 3 人中 “经常运动且不肥胖”的人数为 X ，求随机变量 X 的分布列和数学期望． 附： 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ，其中 n a b c d    ． 20．（本小题满分 12 分） 2 0( )P K K≥ 0.10 0.05 0.01 0.005 0K 2.706 3.811 6.635 7.879 6 如图，已知多面体 ABCDEF 的底面 ABCD 是边长为 2 的正方形， FA  底面 ABCD ， 2AF  ，且 = (0 1)DE AF    ． （1）求证： CE ∥平面 ABF ； （2）若二面角 B CF E  的大小为 5π 6 ，求  的值． 21．（本小题满分 12 分） 已知 O 为坐标原点，椭圆 2 2: 14 xC y  ，点 D M N， ， 为C 上的动点，O M N， ， 三点 共线，直线 DM DN， 的斜率分别为 1 2 1 2( 0)k k k k ， ． （1）证明： 1 2 1 4k k   ； （2）当直线 DM 过点 (1 0)， 时，求 2 2 1 19 | | 2 1DN k   的最小值； （3）若 1 2 0k k  ，证明： 2 2| | | |OD OM 为定值． 22．（本小题满分 12 分） 已知函数 ( ) ln( 1)f x a x  ， ( ) exg x x （ 1x   ）． （1）当 1a  时，证明： ( ) ( )f x x g x≤ ≤ ； （2）设函数 ( ) ( ) ( )F x f x g x  ，若 ( )F x 有极值，且极值为正数，求实数 a 的取值范围． 2021 届江苏基地学校高三第一次大联考 A B C D E F （第 20 题） 7 数学参考答案及评分建议 一、选择题：本题共 8 小题，每小题 5 分，共 40 分。 1~4 D B C D 5~8 C B B C 二、选择题：本题共 4 小题，每小题 5 分，共 20 分。 9．A B 10．A C 11．A B D 12．A C D 三、填空题：本题共 4 小题，每小题 5 分，共计 20 分。 13．8 14． 7 16 15． 2 213 133( )6 36x y   16． 4π 8．【解析】设 2014 年到 2024 年每年的投入资金分别为 1 2 6 1 2 5 a a a b b b， ， ， ， ， ， ．由已知， 1 2 6a a a， ， ， 为等差数列， 1 6160 260 a a， ，其和为 1 1260S 万元； 1 2 5b b b， ， 为等 比数列， 1 260 1.1 b ，公比为 1.1q ，其和为 5 5 2 1.1(1 1.1 )260 2860 (1.1 1)1 1.1     S ． 又 5 5 1 2 2 3 3 5 5 51.1 (1 0.1) 1 0.1 0.1 0.1 1.61         C C C ，所以 2 1744.8S 万元，所以 投资总额大约为 3005 万元．选 C． 12．【解析】对于 A，函数 ( )f x 的最小正周期为 2π ，所以 A 正确； 对于 B，令 ( ) 0f x ，得 2sin 3 sin 2 x x ，函数 ( )f x 的零点个数可转化为两函数 2sin 3 sin 2  y x y x， 图象交点个数，画图可知，图象在  ， 上有只有 2 个交点， 所以 B 错误； 对于 C，由 (2π ) 3+2sin sin 2  f x x x ，所以 (2π ) ( ) 2 3  f x f x ，所以函数 ( )f x 的 图象关于 ( 3)， 对称，C 正确； 对于 D，由 ( ) 2cos 2cos2 2(cos 1)(2cos 1)      f x x x x x ，取一个周期  ， ， 令 ( ) 0 f x ，得 03 3   x ， ， ，且当 3      x ， 时， ( ) 0 f x ，当 3 3      x ， 时， ( ) 0 f x ，当 3     x ， 时， ( ) 0 f x ，所以函数 ( )f x 在 3  x 时取极大值． 由于 5 3( ) (π) 33 2    f f ，所以函数 ( )f x 的最大值为 5 3 2 ，D 正确． 所以本题选 ACD． 8 16．【解析】四个小三角形的顶点所在平面截球面得小圆的的半径 为 2 2 ，小圆面到底座的距离为 2 2 ．设球的半径为 R ， 由条件，得 2 21 2 12 2    R R ，解得 1R ， 所以水晶球的表面积为 4π m2． 四、解答题：本题共 6 小题，共 70 分。 17．（本小题满分 10 分） 【解】若选①，由 3 sin cosc A a C 及正弦定理 sin sin a c A C ， 得 3sin sin sin cosC A A C ，所以 3tan 3C  ． …… 3 分 因为 0 πC  ，所以 30C   ． …… 5 分 又 105B   ，所以 45A   ， …… 6 分 结合 4c  ，可得 sin 4 2sin c Aa C  ． …… 8 分 所以△ABC 中的面积 1 1sin 4 4 2 sin1052 2S ac B      8 2 (sin 45 cos60 cos45 sin60 )       4 3 4  ． …… 10 分 若选②，由 πtan tanπ tan 14tan( ) 2 34 π 1 tan1 tan tan 4 C CC CC       ， 可得 3tan 3C  ．下同① …… 3 分 若选③，由 2 2 2 3a b c ab   ，得 2 2 2 3cos 2 2 a b cC ab    ， …… 3 分 因为 0 πC  ，所以 30C   ．下同① …… 5 分 18．（本小题满分 12 分） 【解】（1）因为 1n na S  ，所以当 1n  时， 12 1a  ，即 1 1 2a  ． …… 1 分 当 2n≥ 时，有 1 1 1n na S   ，所以 1 1 0n n n na a S S     ， 即 1 1 2n na a  ，即 1 1 2 n n a a   （ 2n≥ ）， 9 所以{ }na 是首项为 1 1 2a  ，公比为 1 2 的等比数列， …… 4 分 所以 11 1 1( ) ( )2 2 2 n n na    ． 所以 12 1 log 2nn n n ab na       ． …… 6 分 （2） 1 1 11 2 1 2 ( 2) 2 ( 2) 1 1 1 2 2 ( 1) 2( 2 ) ( 1) 2 n n n n nn n n n n nc b b n nn n                      ．…… 8 分 所以 1 2 3n nT c c c c     1 2 2 3 1 1 1 1 1 1 1 1 1 1( ) ( )2 2 21 2 2 2 2 2 3 2 2 ( 1) 2n nn n                   1 1 2 1 1 1 1 1 2 41 2 ( 1)2 ( 1) 2n nn n            ， …… 10 分 可知{ }nT 为递增数列，所以 1 1 2 1 1 1 1 3 4 4 16 16(1 1) 2nT T       ≥ ． 又 2 1 0( 1) 2nn    ，所以 1 4nT  ，所以 3 1 16 4nT ≤ ． …… 12 分 19．（本小题满分 12 分） 【解】（1）填表如下： 肥胖 不肥胖 合计 经常运动员工 20 40 60 不经常运动员工 24 16 40 合计 44 56 100 …… 2 分 所以 2 2 100(20 16 24 40) 6.92660 40 44 56K       ． …… 5 分 因为 6.926 6.635 ，所以有 99%的把握认为肥胖与不经常运动有关．…… 6 分 （2）“经常运动且不肥胖”的频率为 40 2 100 5 ． …… 8 分 现随机抽取 3 人，“经常运动且不肥胖”的人数为 X 可能的取值为 0，1，2，3． 0 3 0 3 2 2 27( 0) (1 ) ( )5 5 125P X C    ， 1 2 1 3 2 2 54( 1) (1 ) ( )5 5 125P X C    ， 10 2 1 2 3 2 2 36( 2) (1 ) ( )5 5 125P X C    ， 3 0 3 3 2 2 8( 3) (1 ) ( )5 5 125P X C    ． …… 10 分 所以随机变量 X 的分布列为 X 0 1 2 3 P 27 125 54 125 36 125 8 125 所以 X 的数学期望 27 54 36 8 8 6( ) 0 1 2 3125 125 125 125 125 5E X           ．… 12 分 20．（本小题满分 12 分） 【证】（1）因为 =DE AF  ，所以 //DE AF ， 又因为 DE  平面 ABF ， AF  平面 ABF ， 所以 //DE 平面 ABF ． …… 2 分 因为底面 ABCD 是正方形，所以 //CD AB ， 又因为 CD  平面 ABF ， AB  平面 ABF ， 所以 //CD 平面 ABF ． …… 4 分 因为 CD  平面 CDE ， DE  平面 CDE ， CD DE D ， 所以平面 CDE ∥平面 ABF ． 因为 CE  平面 CDE ， 所以 CE ∥平面 ABF ． …… 6 分 【解】（2）以 A 为坐标原点，分别以 AB ， AD ， AF 所在直线为 x 轴、 y 轴、 z 轴， 建立如图空间直角坐标系． 由 2AB AD AF   得， (0 0 0)A ，， ， (2 0 0)B ，， ， (2 2 0)C ，， ， (0 0 2)F ，， ， (0 2 0)D ， ， ， (0 2 2 )E ，， ． 设平面 BCF 的法向量为 1 1 1 1( )x y z ， ，n ， 由已知得， (2 0 2)FB   ，， ， (2 2 2)FC  ，，- ， 由 1 1 0 0 FB FC        ， ， n n 得 1 1 1 1 1 2 2 0 2 2 2 0. x z x y z       ， 不妨取 1 1x  ，则 1 10 1y z ， ， 从而平面 BCF 的一个法向量为 1 (1 0 1) ，，n ． …… 8 分 z x A B C F 11 设平面 ECF 的法向量为 2 2 2 2( )x y z ， ，n ， 又 ( 2 0 2 )CE   ，， ，由 2 2 0 0 FC CE        ， ， n n 得 2 2 2 2 2 2 2 0 2 2 2 0. x z x y z        ， 不妨取 2 1z  ，则 2 2 1x y   ， ， 所以平面 ECF 的一个法向量为 2 ( 1 1)  ， ，n ． …… 10 分 所以 1 2 2 +1cos , 2 1        n n ． 因为二面角 B EC F  的大小为 5π 6 ， 所以 2 3+1 = 22 1     ，化简得 22 5 2 0    ， 解得 1 2  或 2  （舍去）． …… 12 分 21．（本小题满分 12 分） 【解】（1）由题知 M N， 关于原点对称，则可设 1 1 2 2 2 2( ) ( ) ( )D x y M x y N x y ， ， ， ， ， ． 因为点 D M， 在椭圆 C 上，所以 2 2 2 21 2 1 21 14 4 x xy y   ， ， 所以 2 2 2 21 2 1 21 14 4 x xy y   ， ， 所以 2 2 1 22 2 1 2 1 2 1 2 1 2 2 2 2 2 1 2 1 2 1 2 1 2 (1 ) (1 ) 14 4 4 x x y y y y y yk k x x x x x x x x              ． …… 2 分 （2）设直线 1: ( 1)DM y k x  ，代入 2 2 14 x y  可得， 2 2 2 2 1 1 1(1 4 ) 8 4 4 0k x k x k     ，所以 2 1 1 2 2 1 8 1 4 kx x k    ， 因此 2 2 1 22 2 2 1 2 2 1 2 2 1 8 11 ( ) 1 1 4 k kDN k x x k x x k          ， …… 4 分 因为 1 2 1 4k k   ，所以 2 2 2 2 2 1 1 4 kDN k   ． 设 2 21 (1 )t k    ， ，则 2 2 2 1 19 4 16 82 8| | 22 1 t tDN t tk      ≥ ， 12 等号当仅当 2t  时取，即 2 3k   时取等号． 所以 2 2 1 19 | | 2 1DN k   的最小值为 8． …… 7 分 （3）不妨设 1 20 0k k ， ，由 1 2 1 4k k   ， 1 2 0k k  ， 所以 1 2 1 1 2 2k k  ， ． 8 分 将直线 DM 的方程为 1 1 1 ( )2y y x x   代入 2 2 14 x y  可得， 2 2 1 1 1+4 ( ) 42x x x y      ，即 2 2 2 1 1 1 1 1 12 2(2 ) 4 4 4 0x y x x x y x y       ． 因为 2 2 1 14 4x y  ，所以方程可化为 2 1 1 1 1(2 ) 2 0x y x x x y    ． 所以 1 2 1 12x x x y  ，即 2 12x y  ，所以 2 1 1 2y x  ，即 1 1 1( 2 )2M y x ， ．10 分 所以 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 5| | | | ( ) ( 2 ) ( ) +5 52 4OD OM x y y x x y            ．… 12 分 22．（本小题满分 12 分） 【解】（1）当 1a  时，设 ( ) ln( 1)h x x x   ，所以 1( ) 1 1 1 xh x x x      ， 令 ( ) 0h x  ，得 0x  ． 当 0x  时， ( ) 0h x  ， ( )h x 单调递增； 当 1 0x   时， ( ) 0h x  ， ( )h x 单调递减， 所以 ( ) (0) 0h x h ≥ ，即 ( )f x x≤ ． …… 2 分 又 ( ) (e 1)xg x x x   ，因为 e 1x  与 x 同号（当 0x  时， e 1 0x x   ） 所以 ( ) 0g x x ≥ ，即 ( )x g x≤ ． 综上可知， ( ) ( )f x x g x≤ ≤ ． …… 4 分 （2） ( ) ln( 1) exF x a x x   （ 1x   ），所以 ( ) ( 1)e1 xaF x xx     ． 当 0a≤ 时， ( ) 0F x  ， ( )F x 在 ( 1 )  ， 上单调递减，所以 ( )F x 无极值．5 分 当 0a  时，记 ( ) ( )F x x  ，所以 2( ) ( 2)e 0( 1) xax xx       ， 所以 ( )x 即 ( )F x 在 ( 1 )  ， 上单调递减． 13 又 (0) 1F a   ， 1( 1) 1 eaF a a     ． …… 7 分 ①当 0 1a  时， (0) 0F  ， ( 1) 0F a   ， 所以在 ( 1 )  ， 上存在唯一的 ( 1 0)a   ， ，使得 ( ) 0F   ． 当 1 x    ， ( ) 0F x  ，所以 ( )F x 单调递增； 当 x  ， ( ) 0F x  ，所以 ( )F x 单调递减， 所以 ( )F x 的极大值为 ( ) (0) 0F F   ，符合题意． …… 10 分 ②当 1a  时， (0) 0F  ， ( 1) 0F a   ，同理符合题意． ③当 1a  时，由（1）知 ( ) 0F x ≤ ，不合题意． 综上，实数 a 的取值范围是 0a  且 1a  ． …… 12 分