数学卷·2018届江西省抚州市南城一中高二上学期10月月考数学试卷（文科） （解析版）

数学卷·2018届江西省抚州市南城一中高二上学期10月月考数学试卷（文科） （解析版）

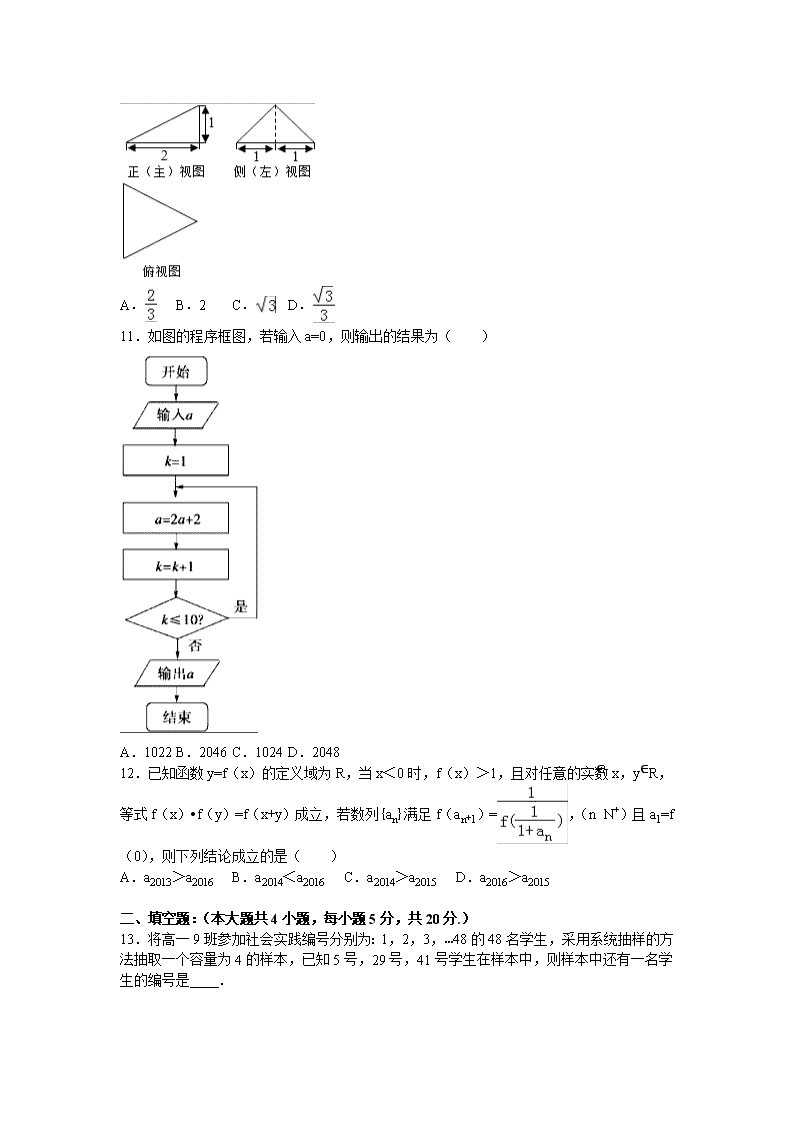
‎2016-2017学年江西省抚州市南城一中高二（上）10月月考数学试卷（文科）‎ ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ ‎1．已知集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}，则A∩B=（　　）‎ A．{x|0＜x＜1} B．{x|0≤x＜1} C．{x|﹣1＜x≤1} D．{x|﹣2＜x≤1}‎ ‎2．函数f（x）=a2x﹣1（a＞0且a≠1）过定点（　　）‎ A．（1，1） B．（，0） C．（1，0） D．（，1）‎ ‎3．函数f（x）=cos（x+）的图象关于（　　）‎ A．原点对称 B．y轴对称 C．直线x=对称 D．直线x=﹣对称 ‎4．已知a→=（﹣2，1），b→=（k，﹣3），c→=（1，2），若（a→﹣2b→）⊥c→，则|b→|=（　　）‎ A．10 B．35 C．32 D．25‎ ‎5．分别在区间[1，6]和[1，4]内任取一个实数，依次记为m和n，则m＞n的概率为（　　）‎ A． B． C． D．‎ ‎6．若变量x，y满足约束条件，则z=2x+y的最大值为（　　）‎ A．0 B．2 C．3 D．4‎ ‎7．若x＞0，y＞0，且2x+y=2，则的最小值是（　　）‎ A．2 B． C． D．‎ ‎8．某公司为确定明年投入某产品的广告支出，对近5年的广告支出m与销售额y（单位：百万元）进行了初步统计，得到下列表格中的数据：‎ y ‎30‎ ‎40‎ p ‎50‎ ‎70‎ m ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 经测算，年广告支出m与年销售额y满足线性回归方程=6.5m+17.5，则p的值为（　　）‎ A．45 B．50 C．55 D．60‎ ‎9．已知等比数列{an}的各项均为正数，公比0＜q＜1，设P=，Q=，则a3，a9，P与Q的大小关系是（　　）‎ A．a3＞P＞Q＞a9 B．a3＞Q＞P＞a9 C．a9＞P＞a3＞Q D．P＞Q＞a3＞a9‎ ‎10．某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）‎ A． B．2 C． D．‎ ‎11．如图的程序框图，若输入a=0，则输出的结果为（　　）‎ A．1022 B．2046 C．1024 D．2048‎ ‎12．已知函数y=f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，等式f（x）•f（y）=f（x+y）成立，若数列{an}满足f（an+1）=，（n∈N+）且a1=f（0），则下列结论成立的是（　　）‎ A．a2013＞a2016 B．a2014＜a2016 C．a2014＞a2015 D．a2016＞a2015‎ ‎　‎ 二、填空题：（本大题共4小题，每小题5分，共20分.）‎ ‎13．将高一9班参加社会实践编号分别为：1，2，3，…48的48名学生，采用系统抽样的方法抽取一个容量为4的样本，已知5号，29号，41号学生在样本中，则样本中还有一名学生的编号是　　．‎ ‎14．已知+=2，则a=　　．‎ ‎15．函数f（x）=2cos2x•（cos2x﹣3sin2x）﹣的最小正周期是　　．‎ ‎16．已知函数f（x）为定义在R上的偶函数，当x≥0时，有f（x+1）=﹣f（x），且当x∈[0，1）时，f（x）=log2（x+1），给出下列命题：‎ ‎①直线y=x与函数f（x）的图象有两个交点；‎ ‎②函数f（x）的值域为（﹣1，1）；‎ ‎③函数f（x）在定义域上是周期为2的函数；‎ ‎④f=0．‎ 其中正确的有　　．‎ ‎　‎ 三、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程.）‎ ‎17．某校在一次期末数学测试中，为统计学生的考试情况，从学校的2000‎ 名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间（满分150分），将统计结果按如下方式分成八组：第一组，如图是按上述分组方法得到的频率分布直方图的一部分．‎ ‎（1）求第七组的频率，并完成频率分布直方图；‎ ‎（2）估计该校的2000名学生这次考试成绩的平均分（可用中值代替各组数据平均值）；‎ ‎（3）若从样本成绩属于第一组和第六组的所有学生中随机抽取2名，求他们的分差小于10分的概率．‎ ‎18．在△ABC中，角A，B，C的对边分别是a，b，c，已知cos2A=﹣，c=，sinA=sinC．‎ ‎（Ⅰ）求a的值；‎ ‎（Ⅱ） 若角A为锐角，求b的值及△ABC的面积．‎ ‎19．已知首项为，公比不等于1的等比数列{an}的前n项和为Sn（n∈N* ），且﹣2S2，S3，4S4成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）令bn=n|an|，数列{bn}的前n项和为Tn，求Tn并比较Tn+bn 与6大小．‎ ‎20．如图，已知在侧棱垂直于底面三棱柱ABC﹣A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点．‎ ‎（1）求证：AC⊥BC1； ‎ ‎（2）求证：AC1∥平面CDB1‎ ‎（3）求三棱锥A1﹣B1CD的体积．‎ ‎21．已知圆C：（x﹣3）2+（y﹣4）2=4，直线l过定点A（1，0）．‎ ‎（1）若l与圆C相切，求l的方程；‎ ‎（2）若l与圆C相交于P、Q两点，若|PQ|=2，求此时直线l的方程．‎ ‎22．已知函数f（x）=ax2﹣（a+1）x+1﹣b（a，b∈R）．‎ ‎（Ⅰ）若a=1，关于x的不等式≥6在区间[1，3]上恒成立，求b的取值范围；‎ ‎（Ⅱ）若b=0，解关于x的不等式f（x）＜0．‎ ‎　‎ ‎2016-2017学年江西省抚州市南城一中高二（上）10月月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ ‎1．已知集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}，则A∩B=（　　）‎ A．{x|0＜x＜1} B．{x|0≤x＜1} C．{x|﹣1＜x≤1} D．{x|﹣2＜x≤1}‎ ‎【考点】交集及其运算．‎ ‎【分析】解不等式求出集合B，代入集合交集运算，可得答案．‎ ‎【解答】解：∵集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}={x|0≤x≤2}，‎ ‎∴A∩B={x|0≤x＜1}，‎ 故选：B．‎ ‎　‎ ‎2．函数f（x）=a2x﹣1（a＞0且a≠1）过定点（　　）‎ A．（1，1） B．（，0） C．（1，0） D．（，1）‎ ‎【考点】指数函数的图象与性质．‎ ‎【分析】由2x﹣1=0得x=，利用a0=1求出函数f（x）=a2x﹣1过的定点坐标．‎ ‎【解答】解：由2x﹣1=0得x=，则f（）=a0=1，‎ ‎∴函数f（x）=a2x﹣1（a＞0且a≠1）过定点（，1），‎ 故选：D．‎ ‎　‎ ‎3．函数f（x）=cos（x+）的图象关于（　　）‎ A．原点对称 B．y轴对称 C．直线x=对称 D．直线x=﹣对称 ‎【考点】余弦函数的图象．‎ ‎【分析】根据三角函数的诱导公式化简函数f（x），得出f（x）是正弦型函数，图象关于原点对称．‎ ‎【解答】解：函数f（x）=cos（x+）=﹣sinx，‎ 所以f（x）是奇函数，其图象关于原点对称．‎ 故选：A．‎ ‎　‎ ‎4．已知a→=（﹣2，1），b→=（k，﹣3），c→=（1，2），若（a→﹣2b→）⊥c→，则|b→|=（　　）‎ A．10 B．35 C．32 D．25‎ ‎【考点】平面向量的坐标运算．‎ ‎【分析】由已知向量垂直得到数量积为0，求出k的值，求出所求向量的模即可．‎ ‎【解答】解：∵=（﹣2，1），=（k，﹣3），=（1，2），且（﹣2）⊥，‎ ‎∴﹣2=（﹣2﹣2k，7），即﹣2﹣2k+14=0，‎ 解得：k=6，‎ ‎∴=（6，﹣3）‎ ‎∴||===3‎ 故选：B．‎ ‎　‎ ‎5．分别在区间[1，6]和[1，4]内任取一个实数，依次记为m和n，则m＞n的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】本题考查的知识点是几何概型的意义，关键是要找出满足条件m＞n的图形面积，及在区间[1，6]和[1，4]内的点对应的面积，再代入几何概型计算公式求解．‎ ‎【解答】解：如图，则在区间[1，6]和[1，4]内任取一个实数，‎ 依次记为m和n，则（m，n）表示的图形面积为3×5=15‎ 其中满足m＞n，即在直线m=n右侧的点表示的图形面积为：，‎ 故m＞n的概率P=，‎ 故选A．‎ ‎　‎ ‎6．若变量x，y满足约束条件，则z=2x+y的最大值为（　　）‎ A．0 B．2 C．3 D．4‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 化目标函数z=2x+y为y=﹣2x+z，‎ 由图可知，当直线y=﹣2x+z过A（2，0）时，直线在y轴上的截距最大，z有最大值为4．‎ 故选：D．‎ ‎　‎ ‎7．若x＞0，y＞0，且2x+y=2，则的最小值是（　　）‎ A．2 B． C． D．‎ ‎【考点】基本不等式在最值问题中的应用．‎ ‎【分析】先根据2x+y=2求得x+=1，进而可把求的最小值转化为求（x+）（）的最小值，然后展开后利用基本不等式求得其最小值．‎ ‎【解答】解：∵2x+y=2‎ ‎∴x+=1‎ ‎∴=（x+）（）=++≥+2=（当且仅当2x2=y2时，等号成立）‎ 故选D ‎　‎ ‎8．某公司为确定明年投入某产品的广告支出，对近5年的广告支出m与销售额y（单位：百万元）进行了初步统计，得到下列表格中的数据：‎ y ‎30‎ ‎40‎ p ‎50‎ ‎70‎ m ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 经测算，年广告支出m与年销售额y满足线性回归方程=6.5m+17.5，则p的值为（　　）‎ A．45 B．50 C．55 D．60‎ ‎【考点】线性回归方程．‎ ‎【分析】求出，代入回归方程计算，从而得出p的值．‎ ‎【解答】解： ==5，‎ ‎∴=6.5×5+17.5=50，‎ ‎∴=50，解得p=60．‎ 故选：D．‎ ‎　‎ ‎9．已知等比数列{an}的各项均为正数，公比0＜q＜1，设P=，Q=，则a3，a9，P与Q的大小关系是（　　）‎ A．a3＞P＞Q＞a9 B．a3＞Q＞P＞a9 C．a9＞P＞a3＞Q D．P＞Q＞a3＞a9‎ ‎【考点】等比数列的性质．‎ ‎【分析】等比数列{an}的各项均为正数，公比0＜q＜1，，可得=＜=P，又各项均为正数，公比0＜q＜1，可得a9＜P＜a3，a9＜Q＜a3．即可得出．‎ ‎【解答】解：等比数列{an}的各项均为正数，公比0＜q＜1，，‎ 则=＜=P，‎ 又各项均为正数，公比0＜q＜1，‎ ‎∴a9＜＜a3，‎ 则a9＜=＜a3．‎ ‎∴a9＜Q＜P＜a3．‎ 故选：A．‎ ‎　‎ ‎10．某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）‎ A． B．2 C． D．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】棱锥的底面积为俯视图三角形的面积，棱锥的高为1，代入体积公式计算即可．‎ ‎【解答】解：由三视图可知几何体为三棱锥，棱锥的底面为俯视图三角形，面积为S==2，棱锥的高h=1，‎ ‎∴棱锥的体积V=Sh==．‎ 故选A．‎ ‎　‎ ‎11．如图的程序框图，若输入a=0，则输出的结果为（　　）‎ A．1022 B．2046 C．1024 D．2048‎ ‎【考点】程序框图．‎ ‎【分析】根据已知的程序框图可得，该程序的功能是利用循环结构计算并输出变量a的值，模拟程序的运行过程，可得答案．‎ ‎【解答】解：∵输入a=0，k=1，‎ 第一次执行循环体后，a=2，k=2，满足继续循环的条件；‎ 第二次执行循环体后，a=6，k=3，满足继续循环的条件；‎ 第三次执行循环体后，a=14，k=4，满足继续循环的条件；‎ 第四次执行循环体后，a=30，k=5，满足继续循环的条件；‎ 第五次执行循环体后，a=62，k=6，满足继续循环的条件；‎ 第六次执行循环体后，a=126，k=7，满足继续循环的条件；‎ 第七次执行循环体后，a=254，k=8，满足继续循环的条件；‎ 第八次执行循环体后，a=510，k=9，满足继续循环的条件；‎ 第九次执行循环体后，a=1022，k=10，满足继续循环的条件；‎ 第十次执行循环体后，a=2046，k=11，不满足继续循环的条件；‎ 故输出的a值为2046，‎ 故选：B ‎　‎ ‎12．已知函数y=f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，等式f（x）•f（y）=f（x+y）成立，若数列{an}满足f（an+1）=，（n∈N+）且a1=f（0），则下列结论成立的是（　　）‎ A．a2013＞a2016 B．a2014＜a2016 C．a2014＞a2015 D．a2016＞a2015‎ ‎【考点】抽象函数及其应用．‎ ‎【分析】先由题意得到f（0）=1=a1，再根据f（an+1）=，得到an+1=﹣，分别求出a1，a2，a3，a4，数列{an}是以3为周期的周期数列，再求出a2013=a3=﹣2，a2014=a1=1，a2015=a2=﹣，a2016=a3=﹣2，即可比较大小 ‎【解答】解：∵f（x）•f（y）=f（x+y）恒成立，‎ ‎∴令x=﹣1，y=0，则f（﹣1）•f（0）=f（﹣1），‎ ‎∵当x＜0时，f（x）＞1，‎ ‎∴f（﹣1）≠0，‎ ‎∴f（0）=1，‎ ‎∵f（an+1）=，∴f（an+1）f（）=1=f（0）‎ ‎∴f（an+1+）=f（0）=a1，‎ ‎∴an+1+=0，‎ 即an+1=﹣，‎ 当n=1时，a2=﹣，‎ 当n=2时，a3=﹣2，‎ 当n=3时，a4=1，‎ ‎∴数列{an}是以3为周期的周期数列，‎ ‎∴a2013=a3=﹣2，‎ a2014=a1=1，‎ a2015=a2=﹣，‎ a2016=a3=﹣2，‎ 故选：B．‎ ‎　‎ 二、填空题：（本大题共4小题，每小题5分，共20分.）‎ ‎13．将高一9班参加社会实践编号分别为：1，2，3，…48的48名学生，采用系统抽样的方法抽取一个容量为4的样本，已知5号，29号，41号学生在样本中，则样本中还有一名学生的编号是　17　．‎ ‎【考点】系统抽样方法．‎ ‎【分析】根据系统抽样的定义，求出样本间隔即可．‎ ‎【解答】解：样本间距为48÷4=12，‎ 则另外一个编号为5+12=17，‎ 故答案为：17．‎ ‎　‎ ‎14．已知+=2，则a=　　．‎ ‎【考点】对数的运算性质．‎ ‎【分析】直接利用导数运算法则化简求解即可．‎ ‎【解答】解： +=2，‎ 可得loga23+loga32=2，‎ 即：loga72=2，‎ 可得a2=72，解得a=6．‎ 故答案为：6．‎ ‎　‎ ‎15．函数f（x）=2cos2x•（cos2x﹣3sin2x）﹣的最小正周期是　　．‎ ‎【考点】三角函数的周期性及其求法．‎ ‎【分析】利用三角恒等变换化简函数的解析式，再利用余弦函数的周期性求得它的最小正周期．‎ ‎【解答】解：函数f（x）=2cos2x•（cos2x﹣3sin2x）﹣=2cos22x﹣6sin2xcos2x﹣‎ ‎=2•﹣3sin4x﹣=2（cos4x﹣sin4x）=2cos（4x+），‎ 故它的最小正周期为=，‎ 故答案为：．‎ ‎　‎ ‎16．已知函数f（x）为定义在R上的偶函数，当x≥0时，有f（x+1）=﹣f（x），且当x∈[0，1）时，f（x）=log2（x+1），给出下列命题：‎ ‎①直线y=x与函数f（x）的图象有两个交点；‎ ‎②函数f（x）的值域为（﹣1，1）；‎ ‎③函数f（x）在定义域上是周期为2的函数；‎ ‎④f=0．‎ 其中正确的有　①②④　．‎ ‎【考点】抽象函数及其应用；函数奇偶性的性质．‎ ‎【分析】根据“当x≥0时，有f（x+1）=﹣f（x）”和赋值法，求出当x≥0时f（x）的周期，设x∈[1，2）则x﹣1∈[0，1），根据条件和恒等式求出f（x）在[1，2）上的解析式，由周期性、偶函数的性质画出函数的图象，根据图象对命题逐一判断即可．‎ ‎【解答】解：∵当x≥0时，有f（x+1）=﹣f（x），‎ ‎∴f（x+2）=﹣f（x+1）=f（x）（x≥0），则当x≥0时，f（x）的周期为T=2．‎ 设x∈[1，2），则x﹣1∈[0，1），‎ ‎∵当x∈[0，1）时，f（x）=log2（x+1），∴f（x﹣1）=log2x，‎ ‎∵当x≥0时，有f（x+1）=﹣f（x），∴f（x）=﹣f（x﹣1）=﹣log2x，x∈[1，2），‎ 又f（x）为定义在R上的偶函数，所以函数f（x）的图象如下图所示：‎ 由图可得：‎ ‎①、直线y=x与函数f（x）的图象有1个交点，故①不正确；‎ ‎②、函数f（x）的值域为（﹣1，1），故②正确；‎ ‎③、函数f（x）在定义域上不是周期函数，故③不正确；‎ ‎④、f=0+0=0，故④正确；‎ 所以正确的命题序号有：①②④‎ 故答案为：①②④．‎ ‎　‎ 三、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程.）‎ ‎17．某校在一次期末数学测试中，为统计学生的考试情况，从学校的2000‎ 名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间（满分150分），将统计结果按如下方式分成八组：第一组，如图是按上述分组方法得到的频率分布直方图的一部分．‎ ‎（1）求第七组的频率，并完成频率分布直方图；‎ ‎（2）估计该校的2000名学生这次考试成绩的平均分（可用中值代替各组数据平均值）；‎ ‎（3）若从样本成绩属于第一组和第六组的所有学生中随机抽取2名，求他们的分差小于10分的概率．‎ ‎【考点】列举法计算基本事件数及事件发生的概率；频率分布直方图．‎ ‎【分析】（1）根据所有频率之和等于1求出第七组的频率，然后绘图即可；‎ ‎（2）利用平均数计算公式计算即可；‎ ‎（3）一一列举所有满足从中任取2人的所有基本事件，找到分差在以上的基本事件，利用概率公式计算即可 ‎【解答】解：（1）由频率分布直方图知第七组的频率 f7=1﹣（0.004+0.012+0.016+0.03+0.02+0.006+0.004）×10=0.08．直方图如图．﹣﹣﹣﹣﹣‎ ‎（2）估计该校的2 000名学生这次考试的平均成绩为：‎ ‎65×0.04+75×0.12+85×0.16+95×0.3+105×0.2+1 15×0.06+125×0.08+135×0.04=97（分）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎（3）第六组有学生3人，分别记作A1，A2，A3，第一组有学生2人，分别记作B1，B2，则从中任取2人的所有基本事件为（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），（A1，A2），（A1，A3），（A2，A3），（B1，B2），共10个．分差大于表示所选2人来自不同组，其基本事件有6个：（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），所以从中任意抽取2人，‎ 分差小于的概率P=．﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎18．在△ABC中，角A，B，C的对边分别是a，b，c，已知cos2A=﹣，c=，sinA=sinC．‎ ‎（Ⅰ）求a的值；‎ ‎（Ⅱ） 若角A为锐角，求b的值及△ABC的面积．‎ ‎【考点】正弦定理；余弦定理．‎ ‎【分析】（Ⅰ）根据题意和正弦定理求出a的值；‎ ‎（Ⅱ）由二倍角的余弦公式变形求出sin2A，由A的范围和平方关系求出cosA，由余弦定理列出方程求出b的值，代入三角形的面积公式求出△ABC的面积．‎ ‎【解答】解：（Ⅰ）在△ABC中，因为，‎ 由正弦定理，‎ 得．…‎ ‎（Ⅱ） 由得，，‎ ‎ 由得，，‎ 则，‎ 由余弦定理a2=b2+c2﹣2bccosA，‎ 化简得，b2﹣2b﹣15=0，解得b=5或b=﹣3（舍负）．‎ 所以． …‎ ‎　‎ ‎19．已知首项为，公比不等于1的等比数列{an}的前n项和为Sn（n∈N* ），且﹣2S2，S3，4S4成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）令bn=n|an|，数列{bn}的前n项和为Tn，求Tn并比较Tn+bn 与6大小．‎ ‎【考点】数列的求和；数列与不等式的综合．‎ ‎【分析】（Ⅰ）由题意得2S3=﹣2S2+4S4，由此求出公比，从而能求出数列{an}通项公式．‎ ‎（Ⅱ），由此利用错位相减法能求出，并求出．‎ ‎【解答】解：（Ⅰ）由题意得2S3=﹣2S2+4S4，‎ 即（S4﹣S2）+（S4﹣S3）=0，亦即（a4+a3）+a4=0，‎ ‎∴，∴公比，…4分 于是数列{an}通项公式为．…5分 ‎（Ⅱ），‎ 所以，①‎ ‎，②…8分 ‎①﹣②得，‎ ‎=‎ ‎=，‎ ‎∴，…11分 ‎∴….12分．‎ ‎　‎ ‎20．如图，已知在侧棱垂直于底面三棱柱ABC﹣A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点．‎ ‎（1）求证：AC⊥BC1； ‎ ‎（2）求证：AC1∥平面CDB1‎ ‎（3）求三棱锥A1﹣B1CD的体积．‎ ‎【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定．‎ ‎【分析】（1）由勾股定理得AC⊥BC，由CC1⊥面ABC 得到CC1⊥AC，从而得到AC⊥面BCC1，故AC⊥BC1．‎ ‎（2）连接B1C交BC1于点E，则DE为△ABC1的中位线，得到DE∥AC1，从而得到AC1∥面B1CD．‎ ‎（3）过C作CF⊥AB垂足为F，CF⊥面ABB1A1，面积法求CF，求出三角形DB1A1的面积，代入体积公式进行运算．‎ ‎【解答】（1）证明：在△ABC中，∵AC=3，AB=5，BC=4，‎ ‎∴△ABC为直角三角形，∴AC⊥BC…‎ 又∵CC1⊥平面ABC，∴CC1⊥AC，CC1∩BC=C，‎ ‎∴AC⊥平面BCC1，∴AC⊥BC1． …‎ ‎（2）证明：设B1C与BC1交于点E，则E为BC1的中点，连结DE，则在△ABC1中，DE∥AC1，‎ 又DE⊂面CDB1，AC1⊄面CDB1，∴AC1∥平面B1CD． …‎ ‎（3）解：在△ABC中，过C作CF⊥AB，F为垂足，‎ ‎∵平面ABB1A1⊥平面ABC，且平面ABB1A1∩平面ABC=AB，∴CF⊥平面ABB1A1，‎ 而，‎ ‎∵，而，‎ ‎∴． …‎ ‎　‎ ‎21．已知圆C：（x﹣3）2+（y﹣4）2=4，直线l过定点A（1，0）．‎ ‎（1）若l与圆C相切，求l的方程；‎ ‎（2）若l与圆C相交于P、Q两点，若|PQ|=2，求此时直线l的方程．‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】（1）分直线的斜率存在和不存在两种情况，分别根据直线和圆相切的性质求得直线的方程，综合可得结论．‎ ‎（2）用点斜式设出直线的方程，利用条件以及点到直线的距离公式，弦长公式求出斜率的值，可得直线的方程．‎ ‎【解答】解：（1）若直线l的斜率不存在，则直线l：x=1，符合题意．‎ 若直线l斜率存在，设直线l的方程为y=k（x﹣1），即kx﹣y﹣k=0．‎ 由题意知，圆心（3，4）到已知直线l的距离等于半径2，即： =2，解之得k=，‎ 此时直线的方程为3x﹣4y﹣3=0．‎ 综上可得，所求直线l的方程是x=1或3x﹣4y﹣3=0．‎ ‎（2）直线与圆相交，斜率必定存在，且不为0，设直线方程为kx﹣y﹣k=0，‎ 因为|PQ|=2=2=2，求得弦心距d=，‎ 即=2，求得 k=1或k=7，‎ 所求直线l方程为x﹣y﹣1=0或7x﹣y﹣7=0．‎ ‎　‎ ‎22．已知函数f（x）=ax2﹣（a+1）x+1﹣b（a，b∈R）．‎ ‎（Ⅰ）若a=1，关于x的不等式≥6在区间[1，3]上恒成立，求b的取值范围；‎ ‎（Ⅱ）若b=0，解关于x的不等式f（x）＜0．‎ ‎【考点】二次函数的性质．‎ ‎【分析】（Ⅰ）通过a=1，化简关于x的不等式≥6，在区间[1，3]上恒成立，利用二次函数的性质求解闭区间上的最小值，求解b的取值范围；‎ ‎（Ⅱ） 当b=0时，不等式f（x）＜0化为（ax﹣1）（x﹣1）＜0，通过①当a=0时，②当a＜0时，③当a＞0时，若a=1；若a＞1，若0＜a＜1，求解不等式解集即可．‎ ‎【解答】解：（Ⅰ）函数f（x）=ax2﹣（a+1）x+1﹣b，a=1，关于x的不等式≥6，‎ 化为：，在区间[1，3]上恒成立，即x2﹣8x+1≥b，在区间[1，3]上恒成立，‎ y=x2﹣8x+1的对称轴为：x=4，开口向上，函数在[1，3]是减函数，最小值为：f（3）=﹣14．‎ 所以b的取值范围为（﹣∞，﹣14]．‎ ‎（Ⅱ） 当b=0时，不等式f（x）＜0化为（ax﹣1）（x﹣1）＜0，‎ ‎①当a=0时，不等式解集为（1，+∞）；‎ ‎②当a＜0时，不等式解集为；‎ ‎③当a＞0时，不等式f（x）＜0化为，‎ 若a=1，不等式解集为∅；若a＞1，不等式解集为；若0＜a＜1，不等式解集为．‎ 综上所述：‎ ‎①当a＜0时，不等式解集为；‎ ‎②当a=0时，不等式解集为（1，+∞）；‎ ‎③当0＜a＜1时，不等式解集为；‎ ‎④当a=1时，不等式解集为∅；‎ ‎⑤当a＞1时，不等式解集为．‎ ‎　‎