- 2021-06-10 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2019届河北省邯郸市第二中学高二上学期期中考试数学试题(解析版)x
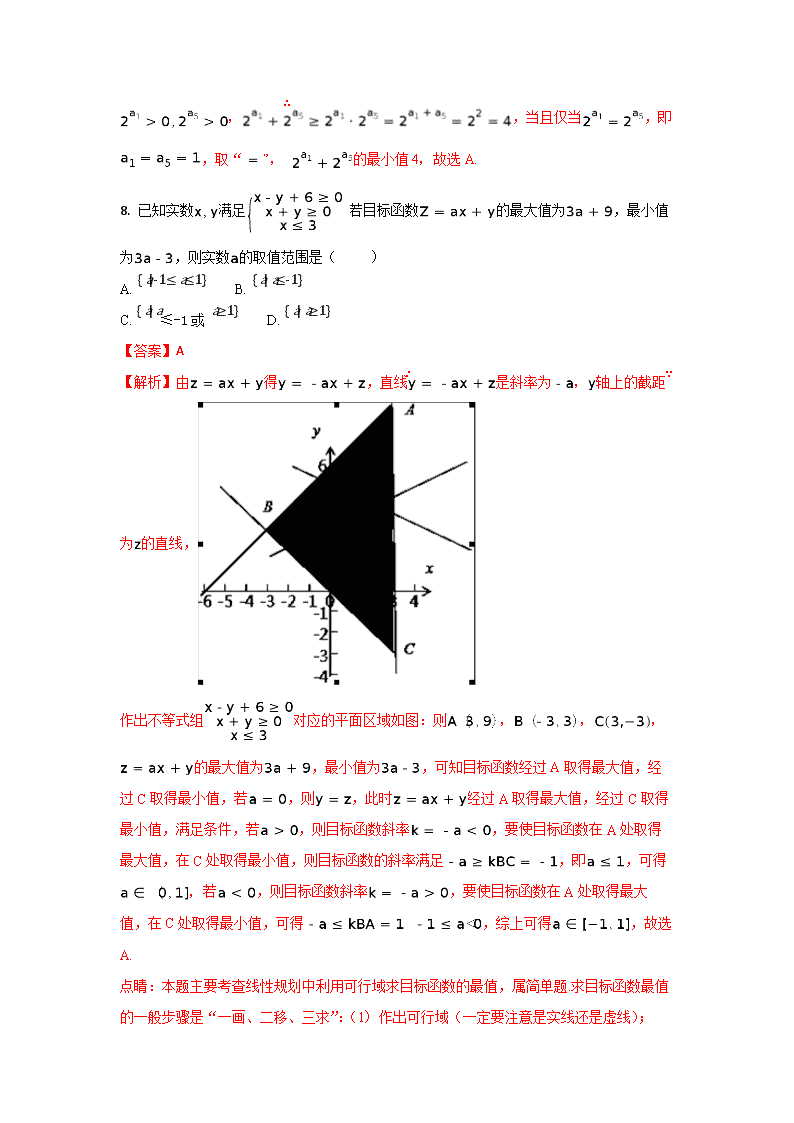
邯郸市第二中学高二年级(2016级)期中考试 数学试卷 一、选择题(本大题共12小题,共60.0分) 1. 已知集合,集合,则( ) A. [3,+∞) B. (3,+∞) C. (-∞,-1]∪[3,+∞) D. (-∞,-1)∪(3,+∞) 【答案】A 【解析】由,得:,,则[3,+∞),故选A. 2. 已知等差数列中,,则( ) A. 20 B. 30 C. 40 D. 50 【答案】A 【解析】设等差数列的公差为,由题意可得:,即,故,故选A. 3. 在中,若,则此三角形为( ) A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 等腰直角三角形 【答案】C 【解析】在中,由以及正弦定理可知,,即,∵,,∴,,所以三角形为直角三角形,故选C. 4. 已知命题,命题,则命题是命题的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 【答案】A 【解析】由,得或,∴命题,解得,由于成立,不成立,即命题是命题的充分不必要条件,故选A. 5. 在公差不为零的等差数列中,,数列是等比数列,且,则( ) A. 1 B. 2 C. 4 D. 8 【答案】C 【解析】∵数列为等差数列,∴,∵,∴,∵,∴,∵数列是等比数列,∴,故,故选C. 6. 下列函数中,最小值为4的是( ) A. B. C. () D. 【答案】B 【解析】时,,,不满足题意; B.由于,由均值不等式可得,当且仅当时取等号,故其最小值为4,满足题意;C.令,则,,因此函数单调递减,∴,不满足题意;D.当时,,不满足题意;故选B. 点睛:本题主要考查了基本不等式.基本不等式求最值应注意的问题(1)使用基本不等式求最值,其失误的真正原因是对其前提“一正、二定、三相等”的忽视.要利用基本不等式求最值,这三个条件缺一不可.(2)在运用基本不等式时,要特别注意“拆”“拼”“凑”等技巧,使其满足基本不等式中“正”“定”“等”的条件 7. 等差数列的前n项和为Sn,若S5=5,那么的最小值为( ) A. 4 B. 2 C. 2 D. 【答案】A 【解析】由等差数列的前项和公式,即,由 ,,当且仅当,即,取“”,∴的最小值4,故选A. 8. 已知实数满足若目标函数的最大值为,最小值为,则实数的取值范围是( ) A. {a|-1≤a≤1} B. {a|a≤-1} C. {a|a≤-1或a≥1} D. {a|a≥1} 【答案】A 【解析】由得,直线是斜率为,轴上的截距为的直线, 作出不等式组对应的平面区域如图:则,,,∵的最大值为,最小值为,可知目标函数经过A取得最大值,经过C取得最小值,若,则,此时经过A取得最大值,经过C取得最小值,满足条件,若,则目标函数斜率,要使目标函数在A处取得最大值,在C处取得最小值,则目标函数的斜率满足,即,可得,若,则目标函数斜率,要使目标函数在A处取得最大值,在C处取得最小值,可得∴,综上可得,故选A. 点睛:本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线); (2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值. 9. 若,则下列不等式:①|a|>|b|;②;③;④a2<b2中,正确的有( ) A. 1个 B. 2个 C. 3个 D. 4个 【答案】C 【解析】对于①,根据不等式的性质,可知若,则,故正确,对于②若,两边同除以,则,即,故正确,对于③若,则,根据基本不等式即可得到;故正确,对于④若,则,故不正确,故选C. 10. 在△ABC中,内角A,B,C的对边分别为a,b,c,已知,,,则的面积为( ) A. B. C. 或 D. 或 【答案】C 【解析】∵,∴由正弦定理可得,∴,∴,∴,∴,∵,∴或,,,,,∴的面积为,,,,,∴的面积为,故选C. 11. 定义为个正数P1,P2…Pn的“均倒数”,若已知正整数数列{an}的前n项的“均倒数”为,又bn=,则++…+=( ) A. B. C. D. 【答案】C 【解析】试题分析:由题意得的前项和 ,,故选C. 考点:与的关系;裂项相消数列求和. 【易错点睛】本题主要考查了的关系;裂项相消数列求和等知识.用裂项相消法求和应注意的问题:利用裂项相消法求和时,应注意抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两项,后面也剩两项,再就是将通项公式裂项后,有时候需要调整前面的系数,使裂开的两项之差与系数相乘后与原项相等.本题难度中等. 12. 给出下列命题: ①命题“若,则方程()无实根”的否命题; ②命题“在中,,那么为等边三角形”的逆命题; ③命题“若,则”的逆否命题; ④“若,则的解集为”的逆命题. 其中真命题的序号为( ) A. ①②③ B. ①②④ C. ②④ D. ①②③④ 【答案】A 【解析】①命题“若,则方程()无实根”的否命题是“若,则方程()有实根”,是正确的;②命题“中,,那么为等边三角形”的逆命题是“是等边三角形,则”,是正确的;③命题“若,则>0”是正确的,∴它的逆否命题也是正确的;④命题“若,则的解集为”的逆命题是“若的解集为,则,∵不等式的解集为时,∴的解集为,∴逆命题是错误的;∴正确命题有①②③;故选A. 二、填空题(本大题共4小题,共20.0分) 13. 若实数满足,则的最大值是______. 【答案】 【解析】 ,即 ,所以的最大值是-2,故填:-2. 14. 如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为______米. 【答案】 【解析】设,则,,则,∴,故答案为. 15. 若变量满足约束条件,则的最大值为______. 【答案】6 【解析】 做出如图所示可行域,由,可看作与间连线的斜率,由题时斜率最大.故本题填. 点睛:本题为线性规划问题.掌握常见的几种目标函数的最值的求法:①利用截距的几何意义;②利用斜率的几何意义;③利用距离的几何意义.往往是根据题中给出的不等式,求出的可 行域,利用的条件约束,做出图形.数形结合求得目标函数的最值. 16. 设Sn为数列{an}的前项和,已知,对任意,都有,则()的最小值为______. 【答案】 点睛:本题考查了等差数列的通项公式与求和公式、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题;利用递推式可得数列为等差数列,根据等差数列的前项和公式可得的表达式,利用导数判断函数的单调性,一定要注意函数的定义域为正整数. 三、解答题(本大题共6小题,共70.0分) 17. 已知数列是公比为2的等比数列,且成等差数列. (1)求数列的通项公式; (2)记,求数列的前项和. 【答案】(1);(2) 试题解析:(1)由题意可得,即,解得:,∴,∴数列的通项公式为. (2), ==. 18. 在中,已知三内角A,B,C成等差数列,且 (1)求及角的值; (2)设角所对的边分别为a,b,c,且,求的值. 【答案】(1);(2)8 【解析】试题分析:(1)根据等差数列的性质可得,再根据诱导公式和同角的三角函数的关系即可求出;(2)根据正弦定理求出,再根据余弦定理求出. 试题解析:(1)∵成等差数列,∴,又,则B=,∵sin(+A)=,∴cosA=,∴sinA==,∴tanA==; (2)由正弦定理可得=,∴b==7,由余弦定理可得,即,解得或,∵,∴,∴,∴舍去,故. 19. (1)若,,且,求的最小值. (2)已知,满足,求的最小值. 【答案】(1)64;(2) 【解析】试题分析:(1)利用基本不等式的性质即可得出;(2)利用“乘1法”即与基本不等式的性质即可得出. 试题解析:(1)∵x>0,y>0,且+=1∴:1=+=,可得:,当且仅当8x=2y,即x=4,y=16时取等号. 那么:xy≥64故xy的最小值是64. (2)∵x>0,y>0,x+2y=1,那么:=()(x+2y)=1+≥3+2=3+,当且仅当x=y,即x=,y=时取等号,故的最小值是:3+. 20. 解关于的不等式 . 【答案】见解析 【解析】试题分析:(1)第一层先讨论,确定二次不等式对应二次函数的开口方向;(2)时要讨论根和的大小关系,结合三个二次的关系得不等式的解集. 试题解析:当时, 当时,; 当时,; 当时,; 当时,. 考点:二次不等式的解法,分类讨论思想. 21. 命题不等式的解集是.命题:函数在定义域内是增函数,若为假命题,为真命题,求的取值范围. 【答案】 【解析】试题分析:由题意可得p,q真时,a的范围,分别由p真q假,p假q真由集合的运算可得 试题解析:∵命题p:不等式的解集是,∴,解得,∵命题q:函数在定义域内是增函数,∴,解得由为假命题,为真命题,可知一真一假,当真假时,由,当假真时,由,或,综上可知的取值范围为:,或 22. 已知数列的前项和为,,数列满足点在直线上. (1)求数列, 的通项,; (2)令,求数列的前项和; (3)若,求对所有的正整数都有成立的的范围. 【答案】(1),;(2) 【解析】试题分析:(1)通过与作差,进而整理可知数列是首项为、公比为2的等比数列,通过将点代入直线计算可知,进而整理即得结论;(2)利用错位相减法计算即得结论;(3)通过(1)及作差法计算可知数列为单调递减数列,进而问题转化为求的最小值,利用基本不等式计算即得结论. 试题解析:(1)解: ∵,∴,当时,,∴,∴,∴是首项为,公比为2的等比数列,因此,当时,满足,所以,因为在直线上,所以,而,所以. (2)∵,∴③,因此④,③-④得: ,∴ (3)证明:由(1)知,,∵ ,∴数列为单调递减数列;∴当时,即最大值为1,由可得,,而当时,当且仅当时取等号,∴. 点睛:本题主要考查的是等差数列和等比数列通项公式以及数列的前 项和与作差法判断数列的单调性;解题中,在利用的同时一定要注意和两种情况,常见的数列求和的方法有公式法即等差等比数列求和公式,分组求和类似于,其中和分别为特殊数列,裂项相消法类似于,错位相减法类似于,其中为等差数列,为等比数列等. 查看更多