2017-2018学年广东省珠海市珠海二中、斗门一中高一上学期期中联考数学卷

2017-2018学年广东省珠海市珠海二中、斗门一中高一上学期期中联考数学卷

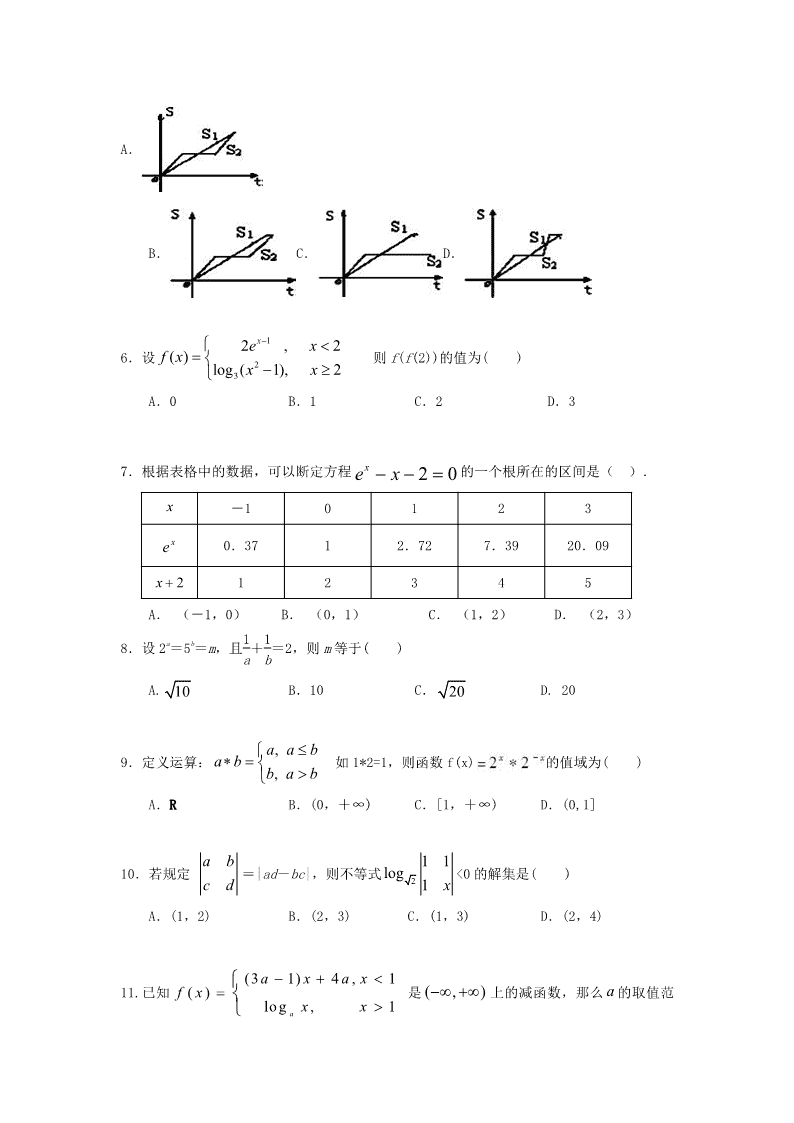
2017-2018 学年广东省珠海市珠海二中、斗门一中高一上学 期期中联考数学卷 考试时间：120 分钟， 总分 150 分， 命题人： 审题人： 第Ⅰ卷（选择题） 一．选择题（本大题共 12 小题，每小题 5 分，共 60 分，每小题给出的四个选项中，只有一 项是符合题目要求的，请将正确的选项填涂到答题卡上） 1．已知全集 U=Z，集合 A={0，1,3}，B={﹣1，0，1，2}，则图中阴影部分所表示的集合为 （ ） A．{﹣l，2} B．{1，0} C．{0，1} D．{1，2} 2．下列各组函数中，表示同一函数的是（ ） A．y=x，y= B．y=lgx 2 ，y=2lgx C．y=|x|，y=（ ） 2 D．y=1，y=x 0 3．已知 f(x5)＝lg x，则 f(2)＝（ ） A． 1 lg 2 5 B． 1 lg5 2 C． 1 lg 2 3 D． 1 lg3 2 4．三个数 3 0.4 ，0.4 3 ，log0.43 的大小关系为（ ） A．0.4 3 ＜log0.43＜3 0.4 B．0.4 3 ＜3 0.4 ＜log0.43 C．log0.43＜3 0.4 ＜0.4 3 D．log0.43＜0.4 3 ＜3 0.4 5． “猫狗赛跑”讲述了这样的故事：领先的小黑狗看着悠闲猫步的小花猫，骄傲起来，睡 了一觉，当它醒来时，发现小花猫快到终点了，于是急忙追赶，但为时已晚，小花猫还是先 到达了终点…，用 S1、S2分别表示小花猫和小黑狗所行的路程，t 为时间，则下图与故事情 节相吻合的是（ ） A． B． C． D． 6．设 1 2 3 2 , 2 ( ) log ( 1), 2 xe x f x x x       则 f(f(2))的值为( ) A．0 B．1 C．2 D．3 7．根据表格中的数据，可以断定方程 2 0xe x   的一个根所在的区间是（ ）． x －1 0 1 2 3 xe 0．37 1 2．72 7．39 20．09 2x  1 2 3 4 5 A． （－1，0） B． （0，1） C． （1，2） D． （2，3） 8．设 2 a ＝5 b ＝m，且 1 a ＋ 1 b ＝2，则 m等于( ) A. 10 B．10 C． 20 D. 20 9．定义运算： , , a a b a b b a b      如 1*2=1，则函数 f(x) 的值域为( ) A．R B．(0，＋∞) C．[1，＋∞) D．(0,1] 10．若规定 a b c d ＝|ad－bc|，则不等式 2 1 1 log 1 x <0 的解集是( ) A．(1，2) B．(2，3) C．(1，3) D．(2，4) 11.已知 (3 1) 4 , 1 ( ) log , 1a a x a x f x x x         是 ( , )  上的减函数，那么 a的取值范 围是（ ） A 1 1 [ , ) 7 3 B. 1 [ , 1 ) 7 C (0,1) D. 1 ( 0 , ) 3 12．若一系列函数的解析式和值域相同，但其定义域不同，则称这些函数为“同族函数”， 例如函数 y＝x2 ，x∈[1,2]与函数 y＝x2 ，x∈[－2，－1]即为“同族函数”．请你找出下面 函数解析式中能够被用来构造“同族函数”的是( ) A．y＝x B．y＝2 x C．y＝ 1 2 log x D．y＝|x－3| 第Ⅱ卷（非选择题） 二．填空题（本大题共 8 小题，每小题 5 分，共 40 分．请将正确答案填在答题卡上） 13．已知 A＝{－1,3，m}，集合 B＝{3,4}，若 B∩A＝B，则实数 m＝________. 14．幂函数 f(x)的图象过点(3， 4 27)，则 f(x)的解析式是 f(x)＝______________． 15．函数 y＝f(x)是定义域为 R 的奇函数，当 x<0 时，f(x)＝x3＋2x－1，则 x>0 时函数的解 析式 f(x) ＝______ ____. 16．已知函数 f(x)，g(x)分别由下表给出： 则不等式 f[g(x)]>g[f(x)]的解集为________． 17. 函数 2 1y x x   的值域是________________ 18．已知函数 f（x）中，对任意实数 a、b都满足：f（a+b）=f（a）+f（b），且 f（2）=3. 则 f（3）= . x 1 2 3 g(x) 3 2 1 x 1 2 3 f(x) 1 3 1 19．在不考虑空气阻力的条件下，火箭的最大速度 vm/s 和燃料的质量 M kg、火箭（除燃料 外）的质量 N kg 的函数关系是 v=2000 ln（1+ M N ）．当燃料质量是火箭质量的 倍时，火箭的最大速度可达 12000m/s． 20．直线 y＝1 与曲线 y＝x2－ |x| ＋a有四个交点，则 a的取值范围为________________． 三．解答题（本大题共 5 小题，每小题 10 分，共 50 分．请将详细解答过程写在答题卡上．） 21．计算：（1） ﹣（﹣9.6） 0 ﹣ +（1.5） ﹣2 ； （2） lg25+lg2﹣lg ﹣log29 × log32． 22．设 2 2{ | 4 0}, { |A x x x B x x     22( 1) 1 0},a x a x R     ，如果 A∩B=B，求实数 a 的取值范围。 23．已知函数 f(x)＝2x＋2ax＋b，且 f(1)＝ 5 2 ，f(2)＝ 17 4 . (1)求 a，b的值； (2)判断函数 f(x)在[0，＋∞)上的单调性，并证明之． 24.已知函数 f（x）=|x﹣1|+|x+1|（x∈R） （1）证明：函数 f（x）是偶函数； （2）利用绝对值及分段函数知识，将函数解析式写成分段函数的形式，然后画出函数图象， 并写出函数的值域； （3）在同一坐标系中画出直线 y=x+2，观察图象写出不等式 f（x）＞x+2 的解集． 25．已知函数 y＝f(x)的定义域为 D，且 f(x)同时满足以下条件： ①f(x)在 D 上是单调递增或单调递减函数； ②存在闭区间[a，b] D(其中 ak. 令 f(x)＝x2 －(2k＋1)x＋k2 －2，得 2k＋1 >k ， 解得－ 9 4

查看更多