云南省云天化中学2019-2020学年高二下学期开学考试数学（文科）试题

云南省云天化中学2019-2020学年高二下学期开学考试数学（文科）试题

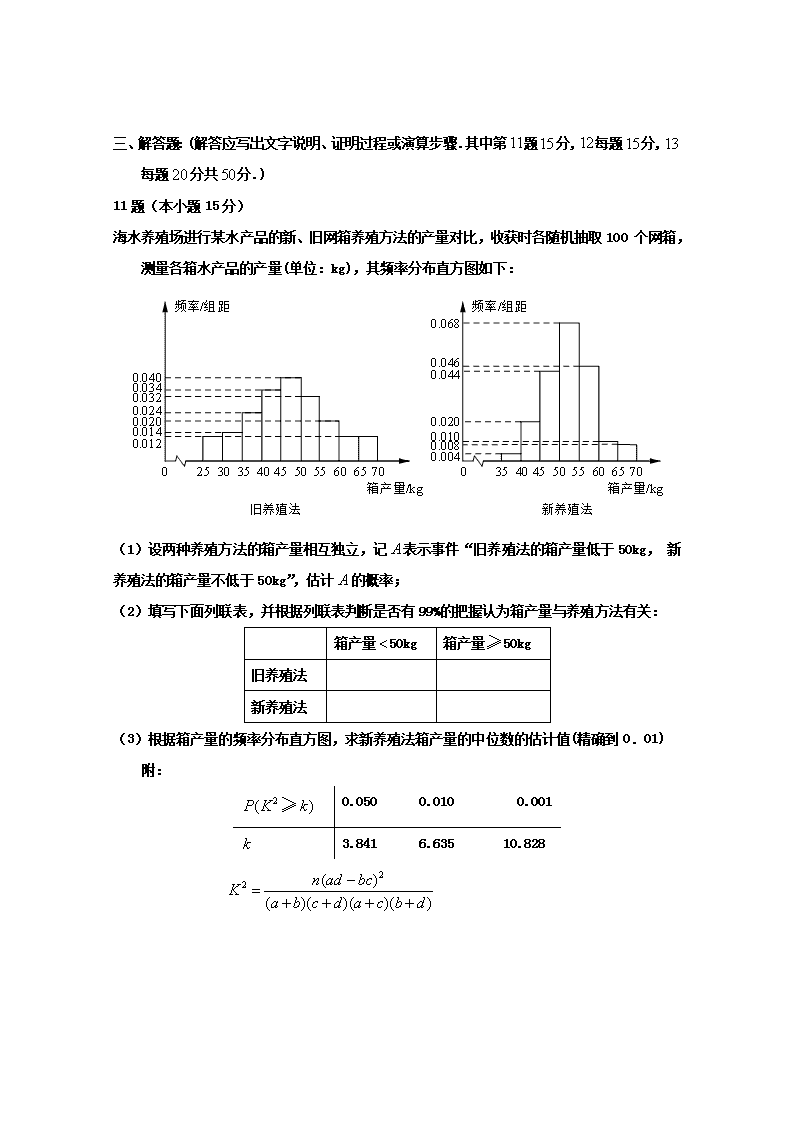
云天化中学2019—2020学年度下学期入学考试 高二年级数学试卷（文科）‎ 第Ⅰ卷（选择题）‎ 一、选择题:（每小题分,共分.每小题只有一个选项符合题意.）‎ ‎1.在复平面内，复数对应的点到直线的距离是 A． B． C． D．1‎ ‎2.用反证法证明命题“设为实数，则方程至少有一个实根”时，要做的假设是 A．方程没有实根 B．方程至多有一个实根 C．方程至多有两个实根 D．方程恰好有两个实根 ‎3.在中，，，分别为内角，，所对的边长，若，，则的面积是 A．3 B． C． D．‎ ‎4.若将函数的图象向右平移个单位，所得图象关于轴对称，则的最小正值是 A． B． C． D．‎ ‎5.某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是，样本数据分组为，，，，．根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是 A．56 B．‎60 ‎ C．120 D．140‎ ‎6.已知椭圆：的左、右顶点分别为，，且以线段为直径的圆与直线相切，则的离心率为 A． B． C． D．‎ ‎ 第II卷（非选择题）‎ 二、 填空题：（每小题分,共分.）‎ ‎7.观察下列等式 ‎1=1‎ ‎2+3+4=9‎ ‎3+4+5+6+7=25‎ ‎4+5+6+7+8+9+10=49‎ ‎……‎ 照此规律，第个等式为 ．‎ ‎8.等差数列的前项和为，，，则 ．‎ ‎9.已知复数（是虚数单位），则．‎ ‎10.记函数 的定义域为．在区间上随机取一个数，则 的概率是 ．‎ 三、解答题：(解答应写出文字说明、证明过程或演算步骤.其中第题分,每题分,每题分共分.)‎ ‎11题（本小题15分）‎ 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取100 个网箱，测量各箱水产品的产量(单位：kg)，其频率分布直方图如下：‎ ‎（1）设两种养殖方法的箱产量相互独立，记表示事件“旧养殖法的箱产量低于‎50kg， 新养殖法的箱产量不低于‎50kg”，估计的概率；‎ ‎（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：‎ 箱产量‎50kg 箱产量‎50kg 旧养殖法 新养殖法 ‎（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值(精确到0．01)‎ 附：‎ ‎0.050 0.010 0.001‎ ‎3.841 6.635 10.828‎ ‎12题（本小题15分）‎ 如图，A，B是海面上位于东西方向相距海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距海里的C点的救援船立即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？‎ ‎13题（本小题20分）‎ 如图，在四棱锥PABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G为线段PC上的点．‎ ‎（Ⅰ）证明：BD⊥面APC ；‎ ‎（Ⅱ）若G是PC的中点，求DG与APC所成的角的正切值；‎ ‎（Ⅲ）若G满足PC⊥面BGD，求 的值．‎ 云天化中学2019—2020学年度下学期入学考试 高二年级数学（文科）参考答案 ‎1.B【解析】　所以复数对应的点为(1,1)，点(1,1)到直线y＝x＋1的距离为＝，故选B.‎ ‎2.A【解析】“至少有一个实根”的反面为“没有实根”，故选A．‎ ‎3.C【解析】由可得①，由余弦定理及可得②．所以由①②得，所以．‎ ‎4.C【解析】，将函数的图象向右平移个单位得 ‎，由该函数为偶函数可知，‎ 即，所以的最小正值是为．‎ ‎5.D【解析】由频率分布直方图可知，这200名学生每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7，故这200名学生中每周的自习时间不少于22.5小时的人数为200×0.7=140．故选D．‎ ‎6.A【解析】以线段为直径的圆是，直线与圆相切，所以圆心到直线的距离，整理为，‎ 即，即 ，，故选A．‎ ‎7. 【解析】把已知等式与行数对应起来，则每一个等式的左边的式子的第一个数是行数，加数的个数是；等式右边都是完全平方数，‎ ‎ 行数 等号左边的项数 ‎1=1 1 1‎ ‎2+3+4=9 2 3‎ ‎3+4+5+6+7=25 3 5‎ ‎4+5+6+7+8+9+10=49 4 7‎ ‎…… …… ……‎ 所以，‎ 即 ‎8.【解析】设等差数列的首项为，公差为，则，‎ 解得，，‎ ‎∴，所以，‎ 所以． ‎ ‎9.【解析】，所以．‎ ‎10.【解析】由，解得，根据几何概型的计算公式得概率为 ‎．‎ ‎11.【解析】（1）记表示事件“旧养殖法的箱产量低于‎50kg”，表示事件“新养殖法的箱产量不低于‎50kg”．‎ 由题意知．‎ 旧养殖法的箱产量低于‎50kg的频率为 故的估计值为．‎ 新养殖法的箱产量不低于‎50kg的频率为 故的估计值为．‎ 因此，事件的概率估计值为．‎ ‎（2）根据箱产量的频率分布直方图得列联表 箱产量‎50kg 箱产量‎50kg 旧养殖法 ‎62‎ ‎38‎ 新养殖法 ‎34‎ ‎66‎ 由于，故有99%的把握认为箱产量与养殖方法有关．‎ ‎（3）因为新养殖法的箱产量频率分布直方图中，箱产量低于‎50kg的直方图面积为 ‎，‎ 箱产量低于‎55kg的直方图面积为 ‎，‎ 故新养殖法箱产量的中位数的估计值为 ‎．‎ ‎12.【解析】由题意知海里，‎ 在中，由正弦定理得 ‎=（海里），‎ 又海里，‎ 在中，由余弦定理得 ‎= ‎ ‎30（海里），则需要的时间（小时）．‎ 答：救援船到达点需要1小时．‎ ‎13.【解析】（Ⅰ）设点O为AC，BD的交点，‎ 由AB＝BC，AD＝CD，得BD是线段AC的中垂线．‎ 所以O为AC的中点，BD⊥AC．‎ 又因为PA⊥平面ABCD，BD平面ABCD，‎ 所以PA⊥BD．所以BD⊥平面APC．‎ ‎（Ⅱ）连结OG.由(1)可知OD⊥平面APC，则DG在平面APC内的射影为OG，所以∠OGD是DG与平面APC所成的角．‎ 由题意得OG＝PA＝.‎ 在△ABC中，AC＝＝，‎ 所以OC＝AC＝.‎ 在直角△OCD中，OD＝＝2.‎ 在直角△OGD中，tan∠OGD＝.‎ 所以DG与平面APC所成的角的正切值为.‎ ‎（Ⅲ）连结OG.因为PC⊥平面BGD，OG平面BGD，所以PC⊥OG.‎ 在直角△PAC中，得PC＝.‎ 所以GC＝.‎ 从而PG＝，‎ 所以.‎