数学理卷·2017湖北省襄阳市第五中学高三第一次适应性考试（2017

数学理卷·2017湖北省襄阳市第五中学高三第一次适应性考试（2017

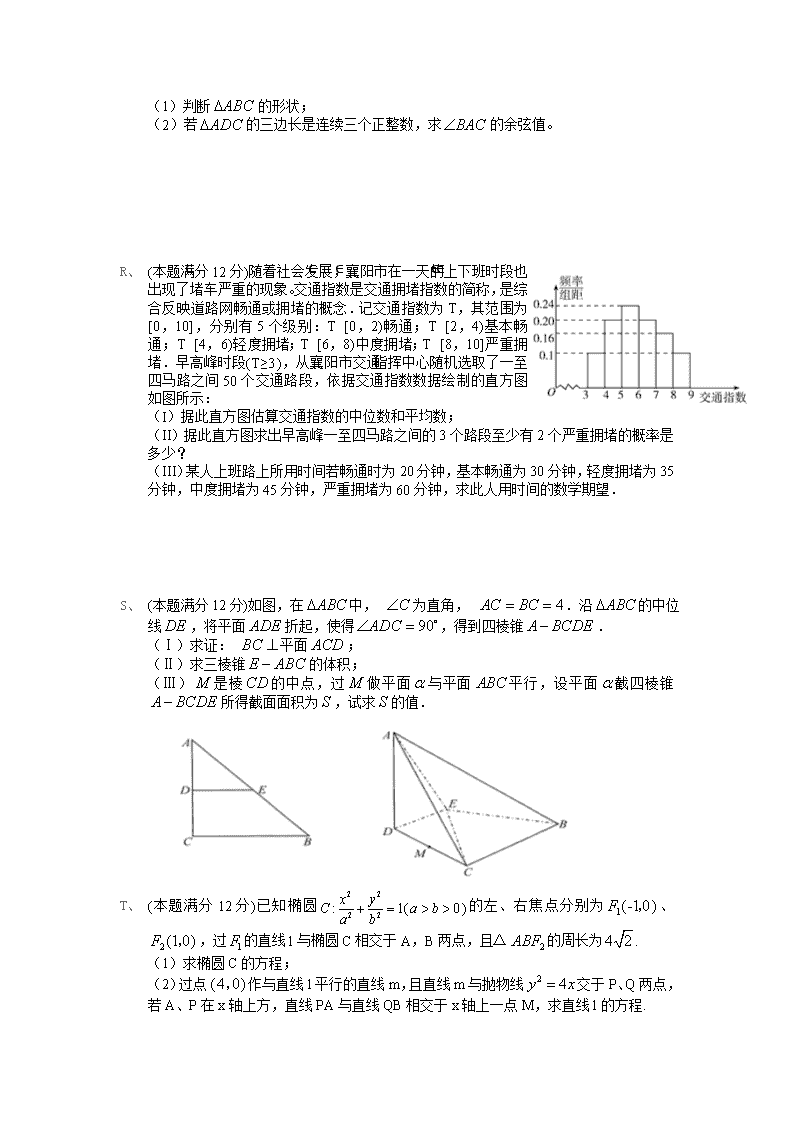
‎2017届襄阳五中高三年级第一次适应性考试 数学（理科） 试 题 命题人：涂圣义 审题人：肖计雄 张华齐 一、选择题（每题5分，满分60分，将答案填在答题纸上）‎ A、 设全集U＝R，集合，则图中阴影部分所表示的集合为（ ） A. 或 B. 或 C. D. ‎ B、 已知是虚数单位，，，、在复平面上对应的点分别为、，则（ ） A．31 B．33 C． D．‎ C、 ‎“” 是“方程表示双曲线”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 D、 下列命题中的假命题是（ ） A. . B. C. D. ‎ E、 李冶（1192--1279 ），真定栾城（今属河北石家庄市）人，金元时期的数学家、诗人，晚年在封龙山隐居讲学，数学著作多部，其中《益古演段》主要研究平面图形问题：求圆的直径、正方形的边长等.其中一问：现有正方形方田一块，内部有一个圆形水池，其中水池的边缘与方田四边之间的面积为13.75亩，若方田的四边到水池的最近距离均为二十步，则圆池直径和方田的边长分别是（注：240平方步为1亩，圆周率按3近似计算）（ ） A．10步，50步 B．20步，60步 C．30步，70步 D．40步，80步 F、 已知， 均为锐角，且，则（ ） A． B． C． D．‎ G、 如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体的三视图，则该几何体的体积为（　　）‎ A． B． C． D．4 ‎ A、 已知向量， ， ，若，则的取值范围是（ ） A． B． C． D．‎ B、 六名大四学生(其中4名男生、2名女生)被安排到A，B，C三所学校实习，每所学校2人，且2名女生不能到同一学校，也不能到C学校，男生甲不能到A学校，则不同的安排方法为(　　) A．24 B．36 C．16 D．18‎ C、 如图，在中，，，点为的中点，将沿折起到的位置，使，连接，得到三棱锥.若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ） A. B. C. D. ‎ D、 已知圆O的半径为定长，点A是平面内一定点（不与O重合），P是圆O上任意一点，线段AP的垂直平分线和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹可能是下列几种：①椭圆，②双曲线，③抛物线，④直线，⑤点 A. ①②⑤ B.①②③ C.①④⑤ D.②③④‎ E、 设函数= x·ex， ， ，若对任意的，都有成立，则实数k的取值范围是 A． B． C． D．‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ F、 已知实数满足，函数的最小值为 ‎ G、 若，则在的展开式中，的幂指数不是整数的项共有 项。 ‎ H、 抛掷红、蓝两颗骰子，设事件A为“蓝色骰子的点数为3或6”，事件B为“两颗骰子的点数之和大于8”．当已知蓝色骰子的点数为3或6时，则两颗骰子的点数之和大于8的概率为______．‎ I、 对于正整数，设是关于的方程的实数根，记，其中表示不超过实数的最大整数，则 .‎ 三、解答题(本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤)‎ D C B A J、 ‎(本题满分12分) 在中，是中点，已知. ‎ ‎（1）判断的形状； （2）若的三边长是连续三个正整数，求的余弦值。 ‎ A、 ‎(本题满分12分)随着社会发展，襄阳市在一天的上下班时段也出现了堵车严重的现象。交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别：T∈[0，2)畅通；T∈[2，4)基本畅通；T∈[4，6)轻度拥堵；T∈[6，8)中度拥堵；T∈[8，10]严重拥堵．早高峰时段(T≥3 )，从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段，依据交通指数数据绘制的直方图如图所示： （I）据此直方图估算交通指数的中位数和平均数； （II）据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少？ （III）某人上班路上所用时间若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为35分钟，中度拥堵为45分钟，严重拥堵为60分钟，求此人用时间的数学期望．‎ ‎ ‎ B、 ‎(本题满分12分)如图，在中， 为直角， ．沿的中位线，将平面折起，使得，得到四棱锥． （Ⅰ）求证： 平面； （Ⅱ）求三棱锥的体积； （Ⅲ）是棱的中点，过做平面与平面平行，设平面截四棱锥所得截面面积为，试求的值．‎ ‎ ‎ C、 ‎(本题满分12分)已知椭圆的左、右焦点分别为、，过的直线l与椭圆C相交于A，B两点，且△的周长为. （1）求椭圆C的方程； （2）过点作与直线l平行的直线m，且直线m与抛物线 交于P、Q两点，若A、P在x轴上方，直线PA与直线QB相交于x轴上一点M，求直线l的方程. ‎ A、 ‎ (本题满分12分)设函数. （1）若函数的图象与直线相切，求的值； （2）当时，求证：.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分。 ‎ B、 选修4-4：坐标系与参数方程 以直角坐标系的原点为极点，轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线的参数方程是（为参数），曲线的极坐标方程是． （1）写出直线的普通方程和曲线的直角坐标方程； （2）设直线与曲线相交于，两点，点为的中点，点的极坐标为，求的值． ‎ C、 选修：不等式选讲. 设函数（，实数）. （1）若，求实数的取值范围； （2）求证： .‎ 数学（理科）参考答案 DACAAB ABBDD AC ‎13． 14．15 15． 16．2017‎ ‎17.解：（I）设 则由 ‎ 中，由正弦定理得 同理得 …………2分 …………4分 即因为 ………………6分 是等腰三角形或直角三角形。 ………………7分 ‎（II）当时， 与的三边长是连续三个正整数矛盾，‎ ， 是等腰三角形。 ………………8分 在直角三角形ADC中，设两直角边分别为 由得n=4， …………10分 由余弦定理或二倍角公式得 或 …………12分 ‎18解析：‎ ‎(1)由直方图知：T∈[4，8)时交通指数的中位数在T∈[5，6)，且为 5＋1×＝ ‎ T∈[4，8)时交通指数的平均数为：………2分 ‎4.5×0.2＋5.5×0.24＋6.5×0.2＋7.5×0.16＝4.72. ………4分 ‎ ‎(2)设事件A为“1条路段严重拥堵”，则P(A)＝0.1，‎ 则3条路段中至少有2条路段严重拥堵的概率为：‎ P＝C32×()2×(1－)＋C33×()3＝，‎ 所以3条路段中至少有2条路段严重拥堵的概率为. …………8分 ‎ ‎(3)由题意，所用时间X的分布列如下表：‎ X ‎30‎ ‎35‎ ‎45‎ ‎60‎ P ‎0.1‎ ‎0.44‎ ‎0.36‎ ‎0.1‎ 则E(X)＝30×0.1＋35×0.44＋45×0.36＋60×0.1＝40.6，‎ 所以此人上班路上所用时间的数学期望是40.6分钟．…………12分 ‎19．（Ⅰ）证明：因为，且，‎ 所以，同时，‎ 又，所以面．‎ 又因为，所以平面．………4分 ‎ ‎（Ⅱ）由（Ⅰ）可知： 平面，又平面，‎ 所以，‎ 又因为，所以．‎ 又因为，所以平面．‎ 所以， ．‎ 依题意， ．‎ 所以， ．…………8分 ‎ ‎（Ⅲ）分别取的中点，并连接，‎ 因为平面平面，所以平面与平面的交线平行于，因为是中点，所以平面与平面的交线是的中位线．同理可证，四边形是平面截四棱锥的截面．‎ 即： ．‎ 由（Ⅰ）可知： 平面，所以，‎ 又∵， ∴．‎ ‎∴四边形是直角梯形．‎ 在中， ∴．‎ ‎， ， ．‎ ‎∴．…………12分 ‎20．解析：（1）依题意，，‎ 所以，‎ 故椭圆C的方程为…………………………4分 ‎（2）设 直线l的方程为：，直线m的方程为 依题意得 则，可得，令，………………6分 由消去x，得，‎ 则，把代入，整理，得① ‎ 由消去x，得，‎ 则，把代入，整理，得②…………10分 由①②消去，得，解得或或 故直线l的方程为：或或…………12分 ‎21．解析：（1），设切点为，‎ 则切线为，即，…………2分 又切线为，所以，‎ 消，得，设，‎ 易得为减函数，且，所以………………4分 ‎（2）令，所以，‎ 当时，，函数在为单调递增；‎ 当时，，函数在为单调递减；‎ 所以，…………………………6分 当时，即时，，‎ 即，故时，在上单调递增，‎ 所以时，，即，所以， ①…………8分 因为，所以，‎ 所以，即， ②………………10分 ‎①+②得：，‎ 故当时，. ……………………12分 ‎22．解析：（1）因为直线的参数方程是（为参数），消去参数得直线的普通方程为．……………………2分 由曲线的极坐标方程，得．‎ 所以曲线的直角坐标方程为．……………………5分 ‎（2）由得，‎ 设，，则的中点，‎ 因为，所以，‎ 又点的直角坐标为，‎ 所以．………………10分 ‎23．解析:‎ ‎（Ⅰ）∵，∴，即，‎ 解得或. ……………………5分 ‎（Ⅱ）, ‎ 当时， ；当时， ；‎ 当时， . ‎ ‎∴，当且仅当即时取等号，∴. ……………………………………12分